Big Bang - Définition

Big Bang ou état stationnaire ?

La découverte de l’expansion de l’univers prouve que celui-ci n’est pas statique, mais laisse place à plusieurs interprétations possibles :

• soit il y a conservation de la matière (hypothèse a priori la plus réaliste), et donc dilution de celle-ci dans le mouvement d’expansion, et dans ce cas l’univers était plus dense par le passé : c’est le Big Bang ;
• soit on peut imaginer à l’inverse que l’expansion s’accompagne d’une création (voire d’une disparition) de matière. Dans ce cadre-là, l’hypothèse la plus esthétique est d’imaginer un phénomène de création continue de matière contrebalançant exactement sa dilution par l’expansion. Un tel univers serait alors stationnaire.

Dans un premier temps, c’est cette seconde hypothèse qui a été la plus populaire, bien que le phénomène de création de matière ne soit pas motivé par des considérations physiques. L’une des raisons de ce succès est que dans ce modèle, appelé théorie de l’état stationnaire, l’univers est éternel. Il ne peut donc y avoir de conflit entre l’âge de celui-ci et celui d’un objet céleste quelconque.

À l’inverse, dans l’hypothèse du Big Bang, l’univers a un âge fini, que l’on déduit directement de son taux d’expansion (voir équations de Friedmann). Dans les années 1940, le taux d’expansion de l’univers était très largement surestimé, ce qui conduisait à une importante sous-estimation de l’âge de l’univers. Or diverses méthodes de datation de la Terre indiquaient que celle-ci était plus vieille que l’âge de l’univers estimé par son taux d’expansion. Les modèles de type Big Bang étaient donc en difficulté vis-à-vis de telles observations. Ces difficultés ont disparu par la suite par une réévaluation plus précise du taux d’expansion de l’univers.

Les problèmes apparents posés par le Big Bang et leur solution

L’étude des modèles de Big Bang révèle un certain nombre de problèmes inhérents à ce type de modèle. En l’absence de modifications, le modèle naïf du Big Bang apparaît peu convaincant, car il nécessite de supposer qu’un certain nombre de quantités physiques sont soit extrêmement grandes, soit extrêmement petites par rapport aux valeurs que l’on pourrait naïvement penser leur attribuer. En d’autres termes, le Big Bang semble nécessiter d’ajuster un certain nombre de paramètres à des valeurs inattendues pour pouvoir être viable. Ce type d’ajustement fin de l’univers est considéré comme problématique dans tout modèle physique (en rapport avec la cosmologie ou pas, d’ailleurs), au point que le Big Bang pourrait être considéré comme un concept posant autant de problèmes qu’il n’en résout, rendant cette solution peu attractive, malgré ses succès à expliquer nombre d’observations. Fort heureusement, des scénarios existent, en particulier l’inflation cosmique, qui, inclus dans les modèles de Big Bang, permettent d’éviter les observations initialement considérées comme étant problématiques. Il est ainsi possible d’avoir aujourd’hui une vision unifiée du contenu matériel, de la structure, de l’histoire et de l’évolution de l’univers, appelée par analogie avec la physique des particules le modèle standard de la cosmologie.

Le problème de l’horizon

Les observations indiquent que l’univers est homogène et isotrope. Il est facile de montrer à l’aide des équations de Friedmann qu’un univers homogène et isotrope à un instant donné va le rester. Par contre, le fait que l’univers soit homogène et isotrope dès l’origine est plus difficile à justifier.

À l’exception d’arguments esthétiques et de simplicité, il n’existe pas a priori de raison valable de supposer que la nature ait choisi que l’univers soit aussi homogène et isotrope que ce que l’on observe. Aucun mécanisme satisfaisant n’explique par ailleurs pourquoi il devrait exister de petits écarts à cette homogénéité, comme ceux qui sont observés dans les anisotropies du fond diffus cosmologique et qui seraient responsables de la formation des grandes structures dans l’univers (galaxie, amas de galaxies, etc.).

Cette situation est insatisfaisante et on a longtemps cherché à proposer des mécanismes qui, partant de conditions initiales relativement génériques, pourraient expliquer pourquoi l’univers a évolué vers l’état observé à notre ère. On peut en effet montrer que deux régions distantes de l’univers observable sont tellement éloignées l’une de l’autre qu’elles n’ont pas eu le temps d’échanger une quelconque information, quand bien même elles étaient bien plus proches l’une de l’autre par le passé qu’elles ne le sont aujourd’hui. Le fait que ces régions distantes présentent essentiellement les mêmes caractéristiques reste donc difficile à justifier. Ce problème est connu sous le nom de problème de l’horizon.

Problème de la platitude

Les différents types de géométries possibles pour l’Univers.

Un autre problème qui apparaît quand on considère l’étude de l’évolution de l’univers est celui de son éventuel rayon de courbure.

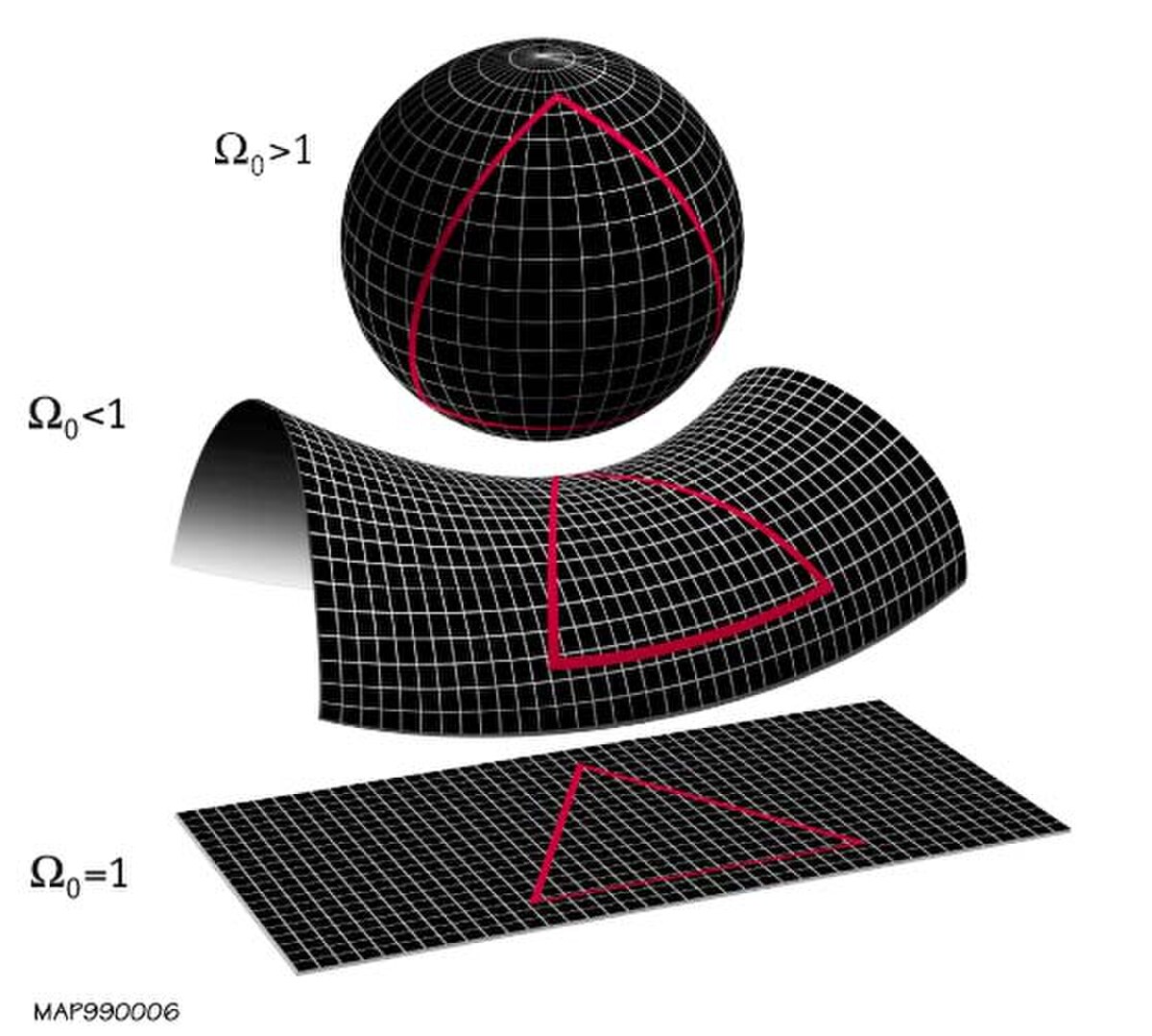
La relativité générale indique que si la répartition de matière est homogène dans l’univers, alors la géométrie de celui-ci ne dépend que d’un paramètre, appelé courbure spatiale. Intuitivement, cette quantité donne l’échelle de distance au-delà de laquelle la géométrie euclidienne (comme le théorème de Pythagore) cesse d’être valable. Par exemple, la somme des angles d’un triangle de taille gigantesque (plusieurs milliards d’années-lumière) pourrait ne pas être égale à 180 degrés. Il reste parfaitement possible que de tels effets, non observés, n’apparaissent qu’à des distances bien plus grandes que celles de l’univers observable.

Néanmoins un problème apparaît si l’on remarque que cette échelle de longueur, appelée rayon de courbure, a tendance à devenir de plus en plus petite par rapport à la taille de l’univers observable. En d’autres termes, si le rayon de courbure était à peine plus grand que la taille de l’univers observable il y a 5 milliards d’années, il devrait être aujourd’hui plus petit que cette dernière, et les effets géométriques sus-mentionnés devraient devenir visibles. En continuant ce raisonnement, il est possible de voir qu’à l’époque de la nucléosynthèse le rayon de courbure devait être immensément plus grand que la taille de l’univers observable pour que les effets dus à la courbure ne soient pas encore visibles aujourd’hui. Le fait que le rayon de courbure soit encore aujourd’hui plus grand que la taille de l’univers observable est connu sous le nom de problème de la platitude.

Problème des monopôles

La physique des particules prévoit l’apparition progressive de nouvelles particules lors du refroidissement résultant de l’expansion de l’univers.

Certaines sont produites lors d’un phénomène appelé transition de phase que l’on pense générique dans l’univers primordial. Ces particules, dont certaines sont appelées monopôles, ont la particularité d’être stables, extrêmement massives (typiquement 10¹⁵ fois plus que le proton) et très nombreuses. Si de telles particules existaient, leur contribution à la densité de l’univers devrait en fait être considérablement plus élevée que celle de la matière ordinaire.

Or, si une partie de la densité de l’univers est due à des formes de matière mal connues (voir plus bas), il n’y a certainement pas la place pour une proportion significative de monopôles. Le problème des monopôles est donc la constatation qu’il n’existe pas en proportion significative de telles particules massives dans l’univers, alors que la physique des particules prédit naturellement leur existence avec une abondance très élevée.

Problème de la formation des structures

Si l’observation révèle que l’univers est homogène à grande échelle, elle révèle aussi qu’il présente des hétérogénéités importantes à plus petite échelle (planètes, étoiles, galaxies, etc.). Le fait que l’univers présente des hétérogénéités plus marquées à petite échelle n’est pas évident en soi. L’on sait expliquer comment, dans certaines circonstances, une petite hétérogénéité dans la distribution de matière peut croître jusqu’à former un objet astrophysique significativement plus compact que son environnement : c’est ce que l’on appelle le mécanisme d’instabilité gravitationnelle, ou instabilité de Jeans (du nom de James Jeans). Cependant, pour qu’un tel mécanisme se produise, il faut supposer la présence initiale d’une petite hétérogénéité, et de plus la variété des structures astrophysiques observées indique que la répartition en amplitude et en taille de ces hétérogénéités initiales suivait une loi bien précise, connue sous le nom de spectre de Harrison-Zeldovitch. Les premiers modèles de Big Bang étaient dans l’incapacité d’expliquer la présence de telles fluctuations. On parlait alors du problème de la formation des structures.

Solutions proposées

Sur le problème de l’horizon

Les problèmes de l’horizon et de la platitude ont une origine commune. Le problème de l’horizon vient du fait qu’à mesure que le temps passe, l’on a accès à des régions de plus en plus grandes, et contenant de plus en plus de matière. Par exemple, avec une expansion dictée par de la matière ordinaire, un nombre croissant de galaxies est visible au cours du temps. Il est donc surprenant que celles-ci possèdent les mêmes caractéristiques.

On se rend compte que ce problème pourrait être résolu si on imaginait qu’une certaine information sur l’état de l’univers ait pu se propager extrêmement rapidement tôt dans l’histoire de l’univers. Dans un tel cas, des régions extrêmement distantes les unes des autres pourraient avoir échangé suffisamment d’information pour qu’il soit possible qu’elles soient dans des configurations semblables. La relativité restreinte stipule cependant que rien ne peut se déplacer plus vite que la lumière, aussi paraît-il difficilement imaginable que le processus proposé soit possible.

Néanmoins, si on suppose que l’expansion de l’univers est très rapide et se fait à taux d’expansion constant, alors on peut contourner la limitation de la relativité restreinte. En effet, dans un tel cas, la distance entre deux régions de l’univers croît exponentiellement au cours du temps, tandis que la taille de l’univers observable reste constante. Une région initialement très petite et homogène va donc avoir la possibilité de prendre une taille démesurée par rapport à la région de l’univers qui est observable. Quand cette phase à taux d’expansion constant s’achève, la région homogène de l’univers dans laquelle nous nous trouvons peut alors être immensément plus grande que celle qui est accessible à nos observations. Quand bien même la phase d’expansion classique reprend son cours, il devient naturel d’observer un univers homogène sur des distances de plus en plus grandes, tant que les limites de la région homogène initiale ne sont pas atteintes. Un tel scénario nécessite que l’expansion de l’univers puisse se faire à taux constant, ou plus généralement de façon accélérée (la vitesse à laquelle deux régions distantes s’éloignent doit croître avec le temps). Les équations de Friedmann stipulent que ceci est possible, mais au prix de l’hypothèse qu’une forme de matière atypique existe dans l’univers (elle doit avoir une pression négative).

Sur le problème de la platitude

Le problème de la platitude peut se résoudre de façon essentiellement identique. Initialement, le problème vient du fait que le rayon de courbure croît moins vite que la taille de l’univers observable. Or ceci peut ne plus être vrai si la loi qui gouverne l’expansion est différente de celle qui gouverne l’expansion d’un univers empli de matière ordinaire. Si en lieu et place de celle-ci l’on imagine qu’une autre forme de matière aux propriétés atypiques existe (que sa pression soit négative), alors on peut montrer que dans un tel cas, le rayon de courbure va croître plus vite que la taille de l’univers observable. Si une telle phase d’expansion s’est produite dans le passé et a duré suffisamment longtemps, alors il n’est plus surprenant que le rayon de courbure ne soit pas mesurable.

Sur le problème des monopôles

Enfin, le problème des monopôles est naturellement résolu avec une phase d’expansion accélérée, car celle-ci a tendance à diluer toute la matière ordinaire de l’univers. Cela amène un nouveau problème : la phase d’expansion accélérée laisse un univers homogène, spatialement plat, sans reliques massives, mais vide de matière. Il faut donc repeupler l’univers avec de la matière ordinaire à l’issue de cette phase d’expansion accélérée.

Le scénario de l’inflation cosmique, proposé par Alan Guth au début des années 1980 répond à l’ensemble de ces critères. La forme de matière atypique qui cause la phase d’expansion accélérée est ce que l’on appelle un champ scalaire (souvent appelé inflaton dans ce contexte), qui possède toutes les propriétés requises. Il peut être à l’origine du démarrage de cette phase accélérée si certaines conditions favorables génériques se trouvent réunies en un endroit de l’univers. À l’issue de cette phase d’expansion accélérée, c’est le champ scalaire lui-même responsable de cette phase d’expansion qui devient instable et se désintègre en plusieurs étapes en particules du modèle standard au cours d’un ensemble de processus complexes appelés préchauffage et réchauffage (voir plus haut).

Les premiers modèles d’inflation souffraient d’un certain nombre de problèmes techniques, notamment les circonstances qui donnaient lieu au démarrage de la phase d’expansion accélérée et à son arrêt étaient peu satisfaisantes. Les modèles d’inflation plus récents évitent ces écueils, et proposent des scénarii tout à fait plausibles pour décrire une telle phase.

Sur la formation des grandes structures

De plus l’inflaton possède, comme toute forme de matière, des fluctuations quantiques (résultat du principe d’indétermination d’Heisenberg). Une des conséquences inattendues de l’inflation est que ces fluctuations, initialement de nature quantique, évoluent durant la phase d’expansion accélérée pour devenir des variations classiques ordinaires de densité. Par ailleurs le calcul du spectre de ces fluctuations effectué dans le cadre de la théorie des perturbations cosmologiques montre qu’il suit précisément les contraintes du spectre de Harrison-Zeldovitch.

Ainsi, l’inflation permet d’expliquer l’apparition de petits écarts à l’homogénéité de l’univers, résolvant du même coup le problème de la formation des structures susmentionné. Ce succès inattendu de l’inflation a immédiatement contribué à en faire un modèle extrêmement attractif, d’autant que le détail des inhomogénéités créées lors de la phase d’inflation peut être confronté aux inhomogénéités existant dans l’univers actuel.

L’accord remarquable entre des prédictions et les observations, observé par l’étude des données relatives aux fluctuations du fond diffus cosmologique observé entre autres par les satellites COBE et WMAP (et bientôt également par le satellite Planck), ainsi que les catalogues de galaxies comme celui réalisé par la mission SDSS est sans nul doute un des plus grands succès de la cosmologie du XX^e siècle.

Il n’en demeure pas moins vrai que des alternatives à l’inflation ont été proposées malgré les succès indéniables de celle-ci. Parmi ceux-ci, citons le pré Big Bang proposé entre autres par Gabriele Veneziano, et l’univers ekpyrotique. Ces modèles sont globalement considérés comme moins génératiques, moins esthétiques et moins achevés que les modèles d’inflation. Ce sont donc ces derniers qui à l’heure actuelle sont de loin considérés comme les plus réalistes.