Construction à la règle et au compas - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Euclide a fondé sa géométrie sur un système d'axiomes qui assure en particulier qu'il est toujours possible de tracer une droite passant par deux points donnés et qu'il est toujours possible de tracer un cercle de centre donné et passant par un point donné. La géométrie euclidienne est donc la géométrie des droites et des cercles, donc de la règle et du compas. L'intuition d'Euclide était que tout nombre pouvait être construit, ou "obtenu", à l'aide de ces deux instruments.
Cette conjecture va d'une part remettre en question la définition d'un nombre : les nombres rationnels ne suffisent pas à exprimer toutes les longueurs puisque la diagonale d'un carré de côté 1 est constructible, mais correspond au nombre √2 dont on démontre facilement qu'il ne saurait être le rapport de deux entiers, d'autre part engager la communauté mathématique dans la recherche de résolutions impossibles, comme la quadrature du cercle, la trisection de l'angle et la duplication du cube. La recherche des nombres constructibles et des polygones constructibles débouchera, après le développement de l'algèbre et de la théorie de Galois, sur le théorème de Gauss-Wantzel sur les polygones constructibles et sur le théorème de Wantzel pour les nombres constructibles.
Georg Mohr (1672) puis Lorenzo Mascheroni (1797) prouveront que toute construction à la règle et au compas peut se réaliser au compas seul.
La règle et le compas en architecture
Les liens qui unissent les constructions à la règle et au compas avec l'architecture sont très étroits :
La géométrie offre plusieurs ressources à l'architecte : elle le familiarise avec la règle et le compas, qui lui servent surtout à déterminer l'emplacement des édifices. (Vitruve)
Au Moyen-Âge, le maître architecte est celui qui possède le savoir de la géométrie, il discute sur un pied d'égalité avec les dirigeants religieux. Dans une société où peu savent lire, le plan, construit à la règle et au compas, est le seul moyen de communication simple entre l'architecte et les ouvriers. Se pose cependant le problème de l'échelle puisque les unités de longueur ne sont pas complètement normalisées. Sur le terrain s'active alors, avec son compas, le parlier ou maître de chantier qui fait le lien entre l'architecte et les ouvriers. Ceux-ci utilisent pour leur construction, un compas et une règle, mais aussi, quand la taille des mesures est trop importante, le cordeau qui remplace indifféremment la règle (trait tiré au cordeau) et le compas. Associés à l'équerre, la règle et le compas deviennent alors le symbole de l'Architecte, maître architecte des cathédrales ou Architecte du monde. Ainsi les retrouve-t-on dans l'emblème de la franc-maçonnerie.
La règle et le compas en géométrie
En géométrie, la règle (non graduée) et le compas sont les outils de base permettant de travailler en géométrie plane. Ils permettent des constructions simples comme celles d'axe ou de centre de symétrie, de parallèle ou de perpendiculaire et sont à l'origine de l'étude des éléments dits remarquables dans un triangle. Mais certaines constructions restent irréalisables comme la construction d'un heptagone régulier ou l'extraction d'une racine cubique.
Médiatrice et bissectrice
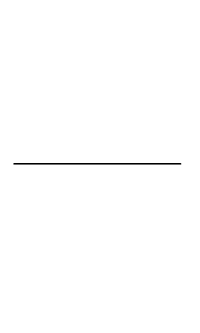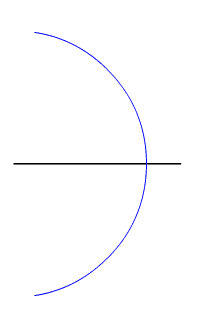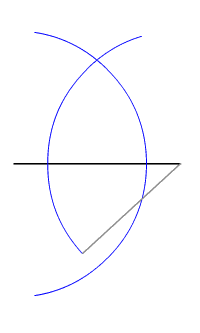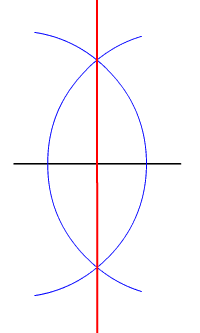
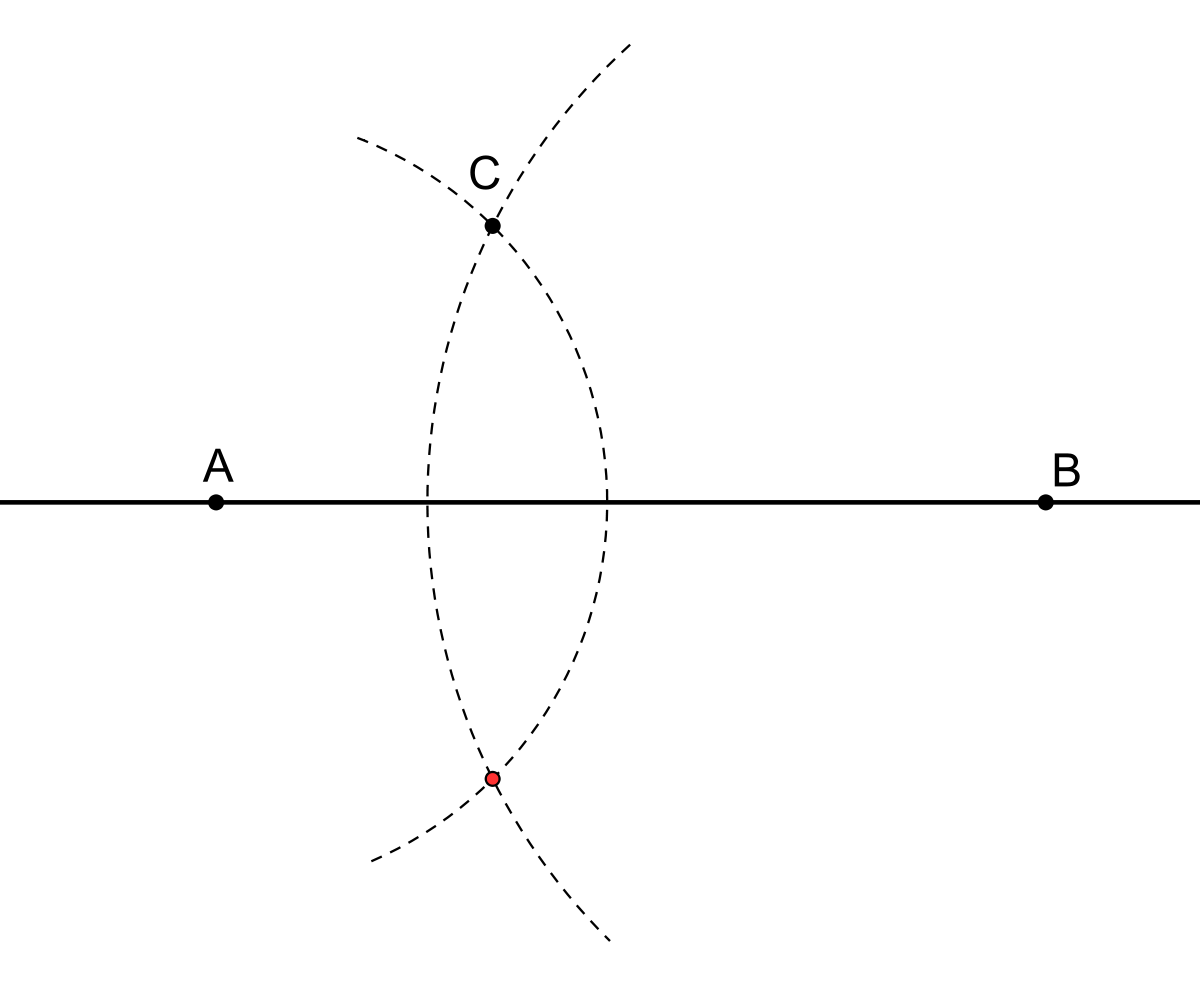
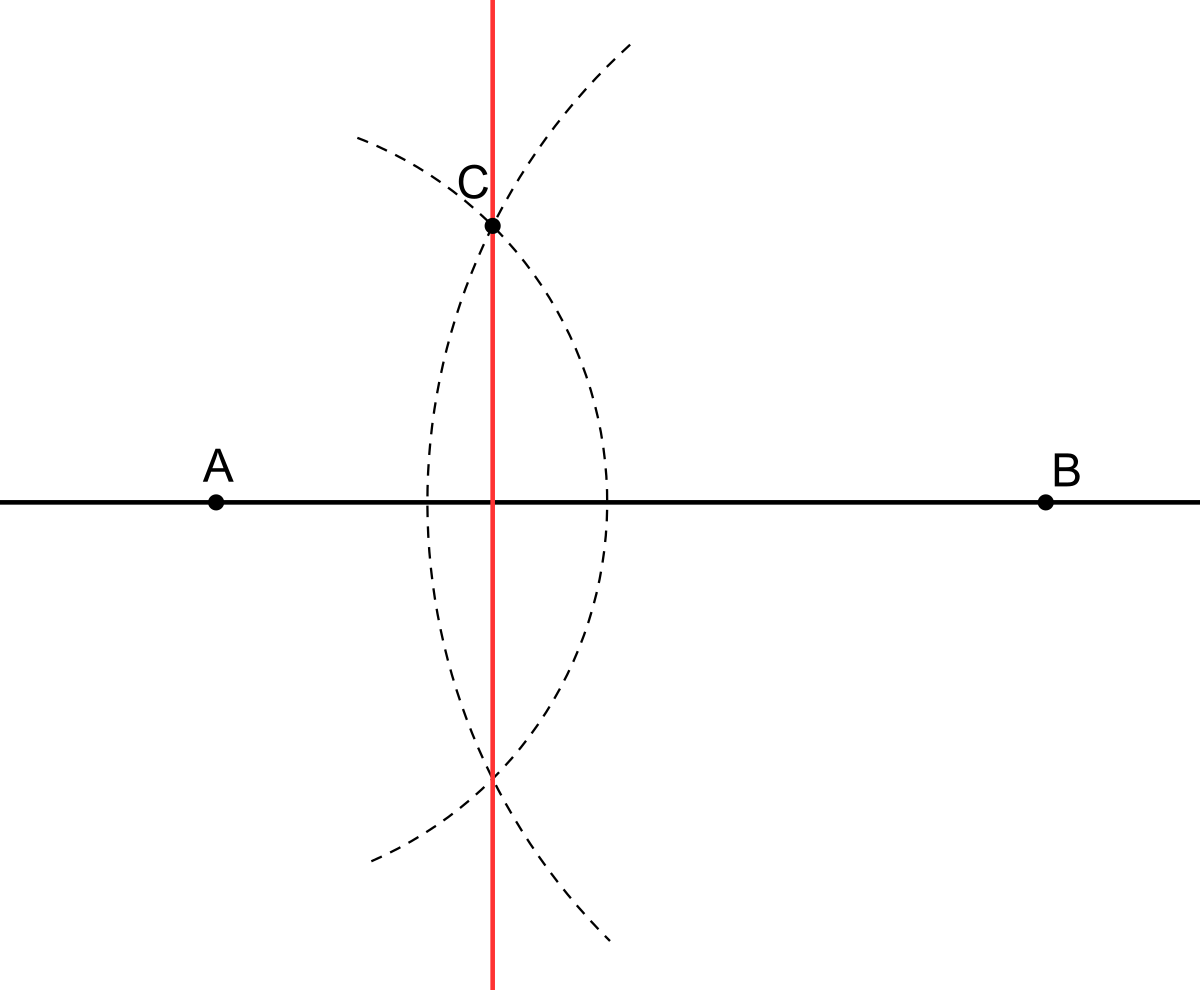
La principale construction de la géométrie est sans doute le tracé de la médiatrice d'un segment. La médiatrice du segment [AB] est la droite d qui coupe perpendiculairement [AB] en son milieu I. mais c'est aussi l'ensemble des points équidistant des extrémités du segment. Il suffit donc d'ouvrir le compas sur une longueur supérieure à la moitié de la longueur du segment, puis de tracer deux cercles avec ce rayon, l'un centré sur A, l'autre sur B (on peut se contenter de ne tracer que des arcs de cercle). L'intersection des deux cercles est constituée de deux points situés à égale distance de A et de B, et qui définissent donc bien la médiatrice.
Cette méthode permet aussi de placer un milieu ou de construire une perpendiculaire.
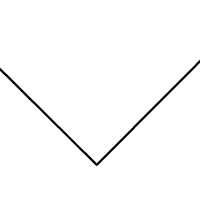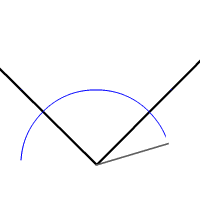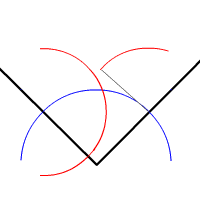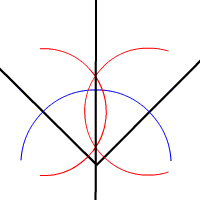
La bissectrice d'un angle, ou plus précisément, d'un secteur angulaire est l'axe de symétrie de ce secteur. Il suffit de construire sur chaque demi-droite deux points à égale distance du sommet en construisant les points d'intersection des demi-droites avec un même cercle de centre le sommet de l'angle. En prenant ces deux points comme centres de deux cercles de même rayon, on construit deux arcs de cercle qui se coupent en deux points appartenant tous deux à la bissectrice recherchée.
Il est donc toujours possible de couper, à la règle et au compas, un angle en deux parts égales. Mais il n'est pas toujours possible de découper, à la règle et au compas, un angle en trois part égales. C'est le problème de la trisection de l'angle.
Milieu et symétriques
Le milieu du segment [AB] s'obtient en construisant le point d'intersection de la droite (AB) avec la médiatrice du segment [AB].
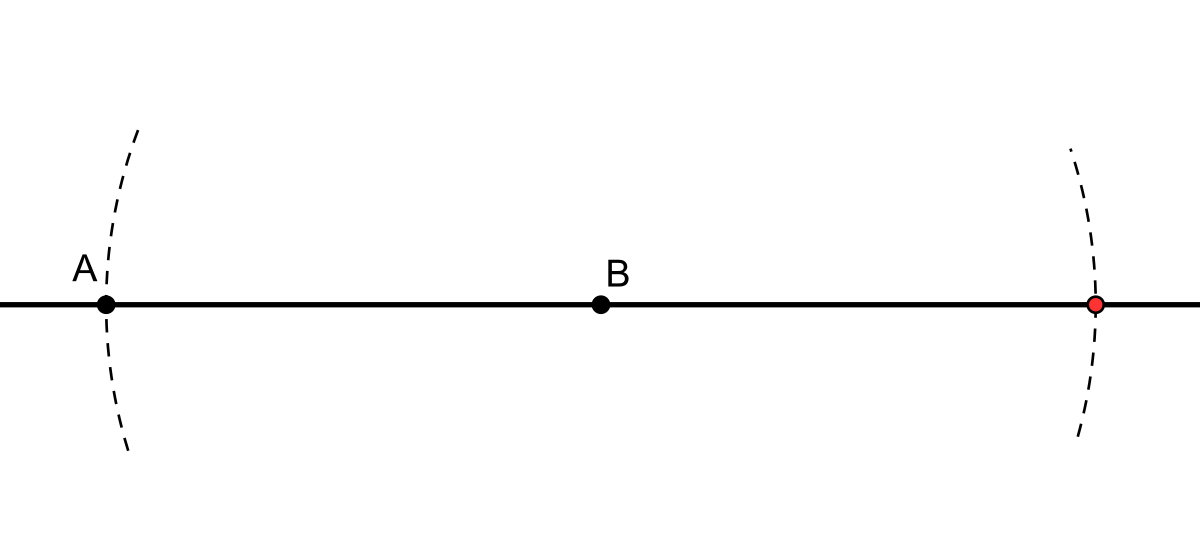
Le symétrique du point A par rapport à B s'obtient en construisant le point d'intersection (différent de A) entre la droite (AB) et le cercle de centre B passant par A.
Le symétrique du point C par rapport à la droite (AB) s'obtient en construisant le point d'intersection (différent de C) entre le cercle de centre A passant par C et le cercle de centre B et passant par C. Si le point C est sur la droite (AB), il est son propre symétrique et aucune construction n'est nécessaire.
Perpendiculaire et parallèle
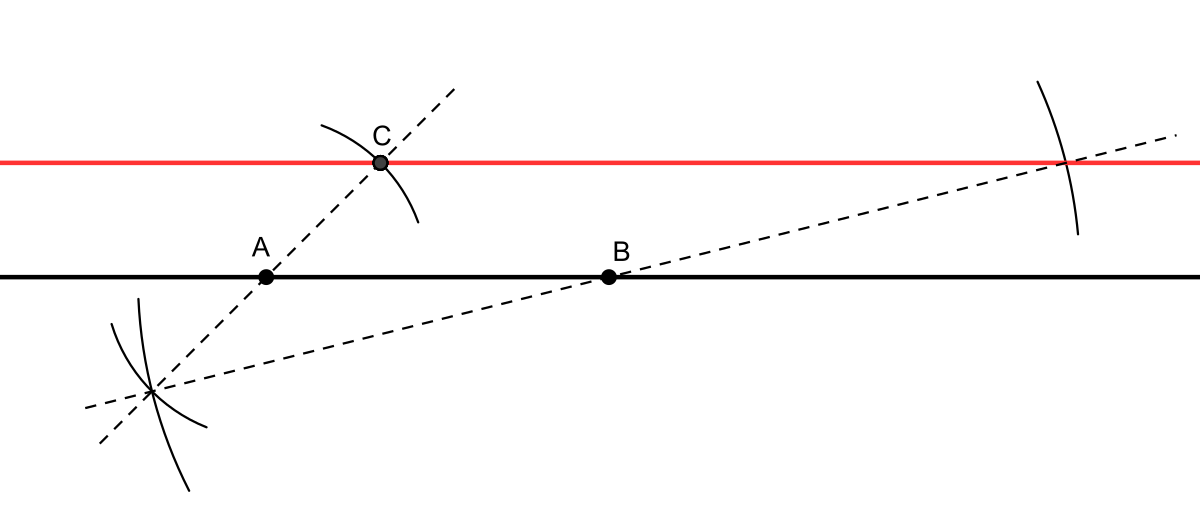
| La parallèle à la droite (AB) passant par un point C se construit à l'aide de la propriété de la droite des milieux. On construit le symétrique C1 du point C par rapport à A puis le symétrique C2 du point C1 par rapport à B. la droite recherchée est la droite (CC2). | La perpendiculaire à la droite (AB) passant par un point C non situé sur (AB) est la droite (CC') joignant le point C à son symétrique par rapport à la droite (AB). Si le point C est situé sur (AB), il suffit de prendre le symétrique A' (ou B') du point A (ou du point B) par rapport à C, la prependiculaire est alors la médiatrice de [AA'] (ou de [BB']) |
Géométrie du triangle
Le triangle est une figure emblématique de la géométrie euclidienne. Tous ses éléments remarquables : bissectrices, médiatrices, hauteurs, médianes, cercle d'Euler et droite d'Euler sont constructibles à la règle et au compas.
Polygones réguliers
Un polygone régulier est un polygone inscriptible dans un cercle et dont tous les côtés sont égaux. Il est aisé de construire à la règle et au compas le triangle, le carré et l'hexagone. Avec plus de difficultés, on peut construire le pentagone. On peut assez facilement doubler le nombre de côtés d'un polygone constructible en traçant des bissectrices et construire, par exemple, des polygones à
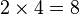
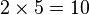
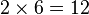
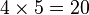
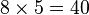
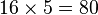
Restent parmi les polygones à moins de 10 côtés, l'heptagone (7 côtés) et l'ennéagone (9 côtés) qui ne sont pas constructibles ; il faudra attendre Gauss, puis Wantzel pour faire l'inventaire de tous les polygones constructibles.
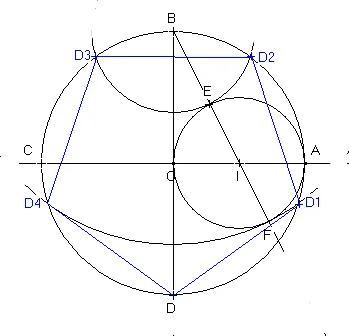
| Construction du pentagone régulier :
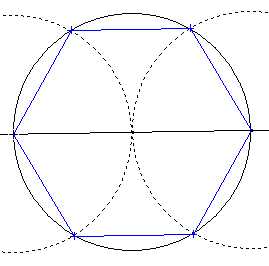
| Construction de l'hexagone régulier : La construction d'un hexagone se fait simplement à l'aide de trois cercles de même rayon. Elle utilise la propriété du triangle équilatéral qui possède trois angles de 60° et le fait que les angles au centre d'un hexagone valent 60°.
|
Nombres constructibles
Pour Euclide, un nombre constructible est un nombre associé à une longueur constructible. De nos jours, un nombre constructible est un nombre obtenu comme coordonnée d'un point constructible à partir d'un quadrillage. On sait maintenant que l'ensemble des nombres constructibles contient l'ensemble des nombres rationnels, mais est strictement inclus dans l'ensemble des nombres algébriques. On sait en particulier que π, nombre transcendant, n'est pas constructible (quadrature du cercle) et que
![\sqrt[3] 2](https://static.techno-science.net/illustration/Definitions/autres/e/eca0e705b1d86d4b1542e5d33b6f1d73_6574bb3a43a9e8353ff471d7cecc061d.png)