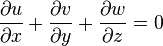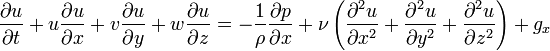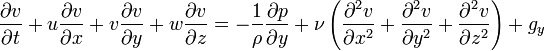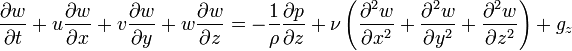Équations de Navier-Stokes - Définition
La liste des auteurs de cet article est disponible ici.
Expression en coordonnées cartésiennes
En coordonnées cartésiennes (x1,x2,x3), les équations de Navier-Stokes s'écrivent :
- Équation de continuité :
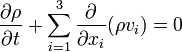
- Équation de bilan de la quantité de mouvement (j = 1,2,3)
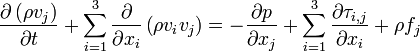
- Équation de bilan de l'énergie
![\frac{\partial \left( \rho e\right)}{\partial t} + \sum_{i=1}^3 \frac{\partial}{\partial x_i} \left[ \; \left(\rho e + p\right) v_i \; \right] = \sum_{i=1}^3 \sum_{j=1}^3 \frac{\partial}{\partial x_i}\left( \tau_{i,j} v_j \right) + \sum_{i=1}^3 \rho f_i v_i - \sum_{i=1}^3 \frac{\partial \dot{q}_i}{\partial x_i} + r](https://static.techno-science.net/illustration/Definitions/autres/3/36175c35e574dd1b15efad57adb0ad88_41f757799a6be3bcf4f14e0b4843cbb1.png)
![\frac{\partial \left( \rho e\right)}{\partial t} + \sum_{i=1}^3 \frac{\partial}{\partial x_i} \left[ \; \left(\rho e + p\right) v_i \; \right] = \sum_{i=1}^3 \sum_{j=1}^3 \frac{\partial}{\partial x_i}\left( \tau_{i,j} v_j \right) + \sum_{i=1}^3 \rho f_i v_i - \sum_{i=1}^3 \frac{\partial \dot{q}_i}{\partial x_i} + r](https://static.techno-science.net/illustrationWebp/Definitions/autres/3/36175c35e574dd1b15efad57adb0ad88_41f757799a6be3bcf4f14e0b4843cbb1.png)
Expression pour les écoulements de fluides incompressibles
Pour un fluide visqueux newtonien et lorsque l'écoulement est incompressible, l'équation de l'énergie est découplée des équations de continuité et de quantité de mouvement, c'est-à-dire qu'on peut déterminer la vitesse et la pression indépendamment de l'équation de l'énergie. L'expression des équations de continuité et de quantité de mouvement sont considérablement simplifiées. On obtient alors
- Équation de continuité appelée alors équation d'incompressibilité
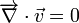
- Équation de bilan de la quantité de mouvement
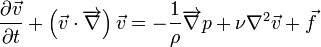
où
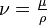
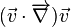
que l'on peut décomposer en coordonnées cartésiennes :
et
Expression pour les écoulements de fluides compressibles
L'écoulement d'un fluide est dit incompressible lorsque l'on peut négliger ses variations de masse volumique au cours du temps. Cette hypothèse est vérifiée lorsque le nombre de Mach Ma est faible. En général, on considère l'écoulement incompressible lorsque Ma < 0.3. Dans le cas contraire, c'est-à-dire pour un écoulement compressible, on adjoint pour fermer le système une équation d'état du fluide, de la forme
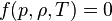
Pour un gaz parfait, cette équation d'état s'écrit
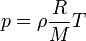
où R désigne la constante des gaz parfaits et M la masse molaire du fluide.
Origine du terme d'advection
Le terme d'advection caractéristique des équations de Navier-Stokes ont une origine mathématique simple inhérente à la relation entre une différentielle totale exacte et les dérivées partielles. En effet, pour une particule fluide l'accélération est donnée par:
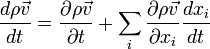
avec ρ la densité du fluide,
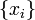
En coordonnées cartésiennes on obtient donc:
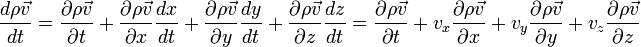
En coordonnées cylindriques de même on obtient:
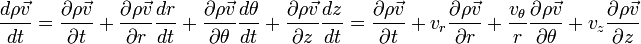
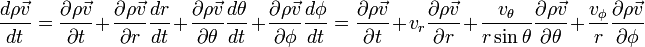
Quelles que soient les coordonnées, on retrouve donc le terme d'advection:
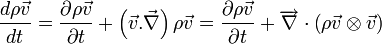
Comme souvent, la formulation de l'accélération sous forme de dérivées partielles permet une recherche plus facile de solutions à des problèmes particuliers, l'intégration de dérivées partielles étant grandement facilitée comparée à des équations comportant des différentielles totales exactes. Ici cette démarche conduit à l'apparition du terme d'advection qui rend compte du transport de matière, découplé de la variation intrinsèque de la vitesse dû à des forces externes au fluide.
Interprétation
L'équation de quantité de mouvement est l'équivalent de la relation fondamentale de la dynamique (aussi appelée seconde loi de Newton) :
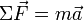
Dans cette formule, on voit apparaître trois types de forces :
- Les forces de pression, spécifique de la mécanique des fluides.
- Les forces de viscosité. Le second terme contenant la viscosité de volume disparait si le fluide est incompressible.
- D'autres forces massiques, qui peuvent être des forces de gravité (
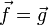
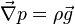
L'expression de l'accélération est plus délicate et s'exprime de deux manières.
- La description lagrangienne consiste à suivre les particules de fluides. L'accélération est la dérivée particulaire de la vitesse : .
- La description eulérienne consiste à se placer en une position fixe. L'accélération est alors la somme de la dérivée partielle de la vitesse
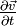
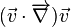
La résolution de l'équation de Navier-Stokes est extrêmement difficile. Elle reste l'une des grandes énigmes mathématiques non résolues à ce jour. Elle fait partie des Problèmes du prix du millénaire.
À la complexité inhérente aux équations aux dérivées partielles s'ajoutent celle de la non-linéarité introduite par le terme d'advection de l'accélération. La plupart du temps, on essaie de résoudre une version simplifiée de l'équation en éliminant l'un de ces termes. Par exemple, à faible nombre de Reynolds, on peut négliger le terme advectif (écoulement de Stokes) et à fort nombre de Reynolds, on s'affranchit de la viscosité (équation d'Euler).
