Figure de la Terre à la Renaissance - Définition

L'aurore de la géodésie moderne

Mesure de la largeur d'une rivière au XVI^e siècle. On se sert d'une triangulation au moyen d'un compas de visée pour faire le levé d'une rivière. On détermine la base d'un triangle par mesure directe à l'aide d'une échelle graduée. On vise ensuite en A un objet remarquable B sur l'autre rive, de manière à ce que l'angle en A soit droit. Enfin, à l'autre extrémité de la base (en D) on détermine l'angle que fait DA avec DB. Ainsi on peut facilement calculer la distance AC au moyen du théorème de Pythagore. L'illustration est tirée d'un livre de Hulsius qui à l'époque constituait le traité le plus complet sur le quadrant et son application en astronomie et en topométrie.

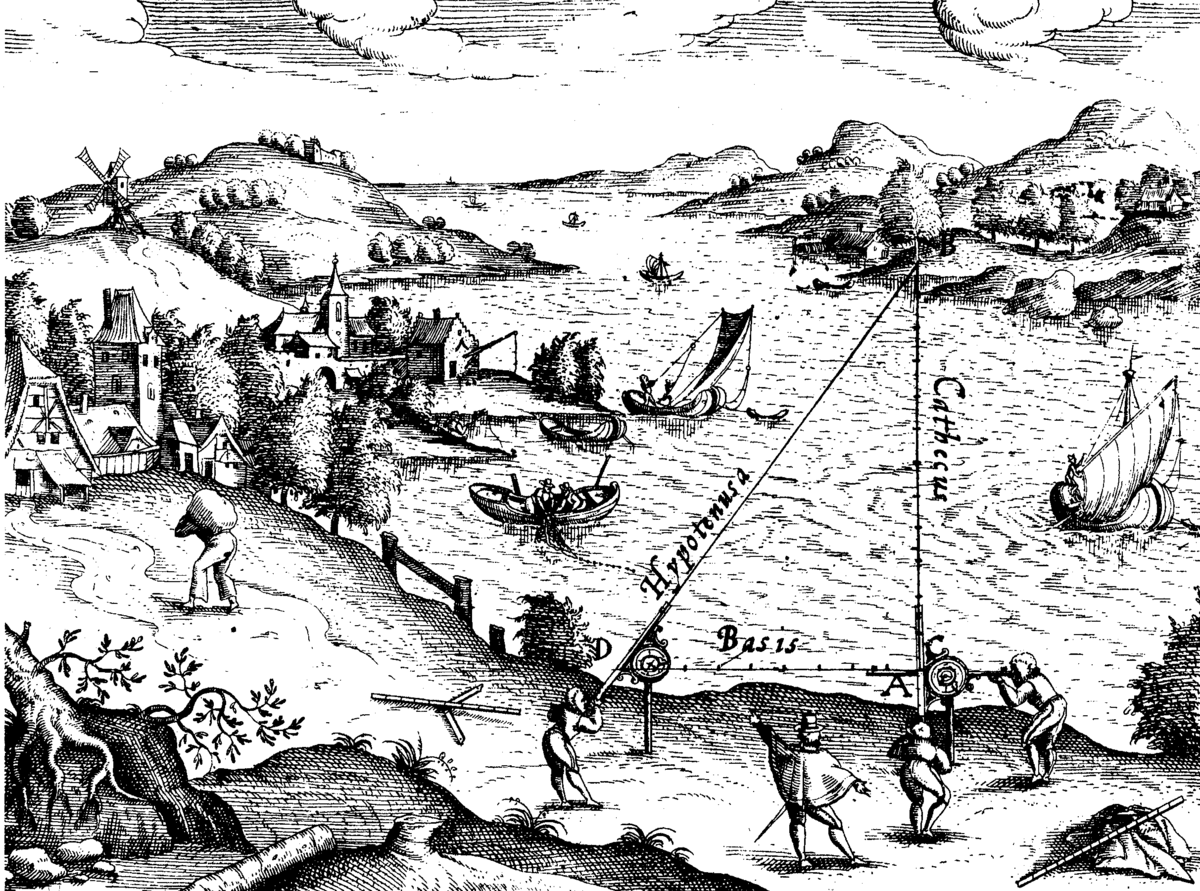
Vers 1615 (ou peut-être 1621), le Hollandais Snellius (Willibrord Snell, 1580–1626) tente de vérifier le résultat de Fernel en procédant à une triangulation entre les villes hollandaises Alkmaar et Bergen op Zoom. Il utilise, pour la première fois au monde dans ce type d'opérations, des lunettes de visée. Il mesure une base dans la région de Leyde. Malgré l'emploi d'instruments optiques, ses résultats ne sont pas bons, puisqu'il détermine le degré de méridien trop court d'environ 3,4%. Cette imprécision est surtout causée par la mauvaise conformation de certains triangles retenus. Néanmoins, la méthode est désormais lancée et fournira au cours des décennies suivantes des mesures précises des dimensions de la Terre. Snell n'est pas le premier à avoir effectué une triangulation géodésique. Nous avons déjà cité celle effectuée au Danemark par Tycho Brahe en 1578. En fait, au XVI^e siècle sont apparues de nouvelles méthodes de topométrie, qui se sont développées en s'appuyant sur des méthodes antiques. En 1528, Sebastian Münster propose de faire un levé trigonométrique simple de l'Allemagne, mais vraisemblablement le premier à effectuer une triangulation fut le Hollandais Rainer Gemma Frisius (1508–1555) ; celle-ci constituait en la mesure de la largeur d'une rivière en 1533, en utilisant pour ce faire des triangles quelconques. Néanmoins, c'est à Snell qu'on doit la première triangulation opérée dans le but avoué de déterminer la circonférence de la Terre.

À cette époque, en 1616 très exactement, l'œuvre de Copernic est mise à l'index des livres proscrits par l'Église catholique. Quelques années plus tard, en 1631, le savant français Pierre Gassendi observe le passage de Mercure devant le Soleil. Il fournit donc un argument sérieux, sinon une preuve, que Mercure tourne autour du Soleil et non autour de la Terre, mais deux ans plus tard, en 1633, commence le procès de Galilée.

En 1637, l'astronome anglais Richard Norwood (1590–1675) mesure la distance de Londres à York au moyen d'une chaîne d'arpenteur et par décompte de pas. Il détermine l'angle au centre correspondant à l'arc de méridien associé à cette distance en observant les hauteurs du Soleil à midi, respectivement à Londres et à York. Il trouve pour la distance L(1°) correspondant à un degré de latitude environ 367196 pieds, c'est-à-dire environ 111,92 kilomètres. Ce résultat est trop grand d'un peu moins de 1%. La même année, en 1637, René Descartes publie les lois de l'optique géométrique, surtout la loi de réfraction. Descartes est déjà connu à cette époque pour plusieurs travaux mathématiques importants. En fait, il déduit la loi exacte de la réfraction, qui s'appelle maintenant « loi de Snell-Descartes » en s'appuyant sur une hypothèse inexacte. Pierre de Fermat (1601–1665) accepte le résultat trouvé par Descartes, mais critique ses fondements théoriques. De la sorte, il est amené à énoncer le fameux principe de tautochronisme, dit « principe de Fermat ». Celui-ci exprime que le chemin parcouru par la lumière est toujours tel qu'il correspond à un temps de parcours extrémum.

L'année après la parution de la loi de la réfraction, Galilée publie ses découvertes fondamentales en mécanique, à savoir celles qui concernent le mouvement uniformément accéléré et la trajectoire des projectiles dans le vide, et il définit la force comme la cause de l'accélération. C'est encore à cette époque que Descartes, Fermat, Roberval et d'autres mettent au point la construction des tangentes aux courbes. Puis, en 1641, Blaise Pascal invente l'arithmomètre, précurseur des machines à calculer et des ordinateurs.

En 1643, Viviani — disciple de Galilée — exécute l'expérience du baromètre de Torricelli (1608–1647), qui met en évidence le poids de l'air et l'existence d'une atmosphère limitée, dont l'expérience de Pascal et Périer, effectuée en 1648 au Puy-de-Dôme, viendra apporter la preuve irréfutable. Tous ces progrès scientifiques vont jouer, à court ou à long terme, un rôle important dans le développement de la géodésie et de la théorie de la figure de la Terre.

En 1661 le père jésuite Giovanni-Baptista Riccioli reprend la mesure de la longueur L(1°) d'un degré de latitude par une méthode différente de celle d'Eratosthène. Elle se base sur la détermination d'angles zénithaux. Riccioli s'était servi déjà de cette méthode en 1645 en collaboration avec Grimaldi. Elle consiste à mesurer en deux sommets P₁ et P₂, de distance connue P₁P₂, les distances zénithales réciproques z₁ et z₂. La somme des angles du triangle P₁OP₂, où O désigne le centre de la Terre, étant égale à 180°, on déduit que l'angle au centre α est fourni par α = z₁ + z₂ – 180°. Cette méthode, indiquée par Kepler, ne pouvait pas fournir de résultats précis à l'époque, et à ce jour-même elle n'est guère recommandée. En effet, la mesure précise des distances zénithales est rendue délicate par la réfraction atmosphérique négligée à tort par Riccioli. Ainsi, sa valeur de 62900 toises pour L(1°) tombait loin de la valeur exacte. En appliquant un coefficient de réfraction convenable, on peut corriger ce résultat a posteriori et le ramener à une valeur comprise entre 55000 et 57000 toises, sans pouvoir préciser davantage.