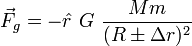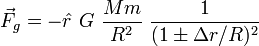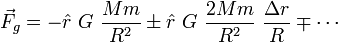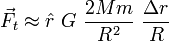Force de marée - Définition

Introduction

La comète Shoemaker-Levy 9 en 1994 après avoir été brisée par les forces de marée de Jupiter au cours d'un passage précédent, en 1992.

La force de marée est une conséquence de la non-uniformité de la force de gravitation exercée sur un corps par l'ensemble des astres qui l'entourent. Notamment, le côté d'un corps le plus près d'un astre subit une plus grande force que le côté le plus éloigné. C'est cette variation de la force de gravitation en deux points d'un même corps qui est appelée terme différentiel de marée ou plus simplement force de marée. Les forces de marée engendrent des contraintes sur les corps impliqués, ce qui les déforme ou peut même les briser : la limite de Roche est la distance entre deux corps à partir de laquelle le plus léger se désintègre.

Les forces de marée sont une manifestation du caractère non galiléen du référentiel géocentrique. Elles sont dues aux forces d'inertie (en l'occurrence une force d'inertie d'entraînement) agissant sur un corps étudié dans ce référentiel et se calculent en considérant le mouvement de translation circulaire du centre de la Terre dans le référentiel héliocentrique.

Système Terre-Lune-Soleil

Les marées océaniques sur la planète Terre

Le champs de gravitation de la lune, dans lequel se trouve la Terre, n’est pas uniforme. Si l’on considère sa variation au centre de la Terre, elle est positive en face de la Lune, négative dans la région opposée, mais dirigée dans le sens contraire. Dans les deux cas, sa variation s’oppose à l’attraction terrestre, alors que sur les côtés, elle vient au contraire la renforcer.

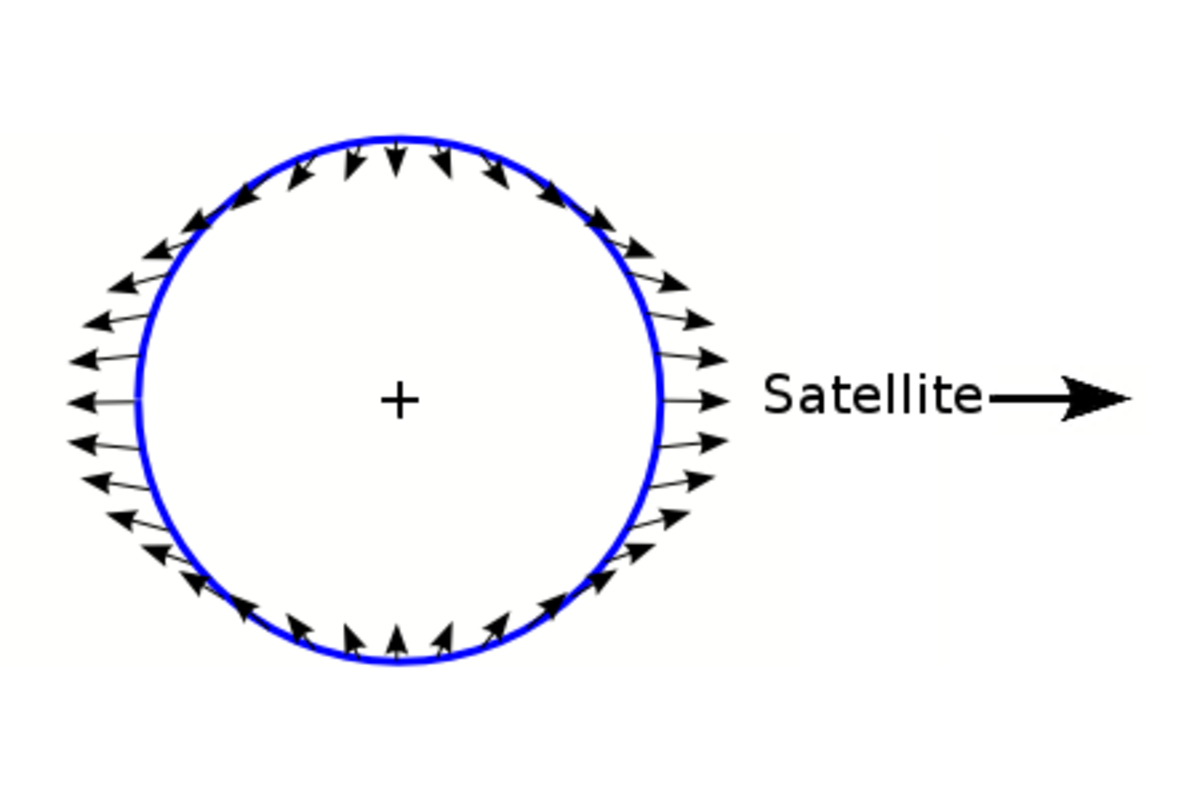
Les marées océaniques sont les grands mouvements des masses océaniques soumises à la gravitation lunaire et, dans une moindre mesure, celle du Soleil.

La force de gravitation exercée par un corps est une force proportionnelle à la masse de ce corps et à l'inverse du carré de la distance m/r² (pour la force exercée par la Lune sur la Terre, m est la masse de la Lune, r est la distance Terre-Lune). La force de marée étant un terme différentiel, elle est proportionnelle à la variation de la force de gravitation par rapport à la distance r, ce qui donne un effet proportionnel à m/r³. C'est cette proportionnalité qui explique que le Soleil, bien que beaucoup plus massif que la Lune, ait néanmoins un effet égal à seulement environ 45% de celui de la Lune car la distance Terre-Lune est bien plus petite que la distance Terre-Soleil.

Sous l'effet du mouvement relatif de la Lune par rapport à la Terre, la force de gravité qui est ressentie à la surface de la Terre varie continuellement. À cause de ces changements, la masse liquide des océans se déforme pour retrouver son point d'équilibre. La modification est relativement faible parce que la Lune orbite relativement loin de la Terre et sa masse est assez faible. Néanmoins, sur une masse liquide et donc facilement déformable comme les océans, ce changement se traduit par une variation du niveau des eaux qui est connue sous le nom de marée.

L'amplitude théorique des marées océaniques est d'environ 1 mètre à l'équateur, mais leur valeur réelle diffère considérablement

• d'abord par un phénomène complexe de résonance. La période propre des océans est relativement longue, environ 30 heures (alors que celui de la croûte terrestre est d'environ 57 minutes). Cela veut dire que si la Lune disparaissait soudain, le niveau des océans oscillerait avec une période de 30 heures et une amplitude décroissant progressivement jusqu'à ce que l'énergie emmagasinée soit dissipée (cette valeur de 30 h est fonction uniquement de la gravité terrestre et de la profondeur moyenne des océans). Et la Lune stimule les océans avec une période d'environ 12,42 heures (la moitié de la période de rotation synodique de la Terre), inférieure à la période propre des masses d'eau, qui réagissent avec retard : le principal effet est que le retard des marées est, en moyenne, de six heures (c'est-à-dire que la marée basse se produit quand la Lune passe au zénith ou au nadir, un résultat tout à fait opposé à l'intuition commune)
• ensuite à cause de la topographie des lieux : avec une configuration en entonnoir (l'ensemble Manche / baie du mont Saint Michel étant l'un des exemple les plus fameux) l'effet de la marée est localement amplifié, inversement une mer fermée comme la Méditerranée connait des marées faibles.

Marées atmosphériques et terrestres

En plus des marées océaniques, il y a des marées atmosphériques ainsi que des marées terrestres, s'exerçant sur la masse rocheuse de la Terre. Les marées atmosphériques sont peu observables, noyées par les effets beaucoup plus importants dus à la météo d'une part et aux marées thermiques solaires d'autre part. La croûte terrestre, elle, se déforme régulièrement de manière peu perceptible en fonction des mouvements lunaires. L'amplitude des marées terrestres est d'environ 1,5 mètre à l'équateur, et elles sont en phase avec la Lune - ce qui fait qu'elles réduisent l'effet apparent des marées océaniques. Ce mouvement incessant s'associe à des phénomènes de stress et donc de fragilisation qui jouent un rôle à long terme dans le déclenchement de certains tremblements de terre. En revanche, quoi qu'en disent les magazines à sensation, même l'alignement de nombreuses planètes du système solaire n'a pas de vraies conséquences observables, et cela en raison de leur distance énorme à la Terre, dont le carré intervient en dénominateur.

De manière générale, on parle de forces de marée pour tous les corps qui subissent ce type de variation de la gravité locale à cause des mouvements d'un corps massif (de préférence sur une orbite à peu près circulaire). Ces forces sont généralement peu sensibles, mais dans un certain nombre de cas, elles peuvent prendre des proportions telles que l'impact en est observable plus facilement.

Précession des équinoxes

En deuxième approximation, la figure de la Terre est ellipsoïdale. Si l'on retranche à l'ellipsoïde la sphère tangente inscrite, il reste un « renflement » ou « bourrelet » équatorial. À cause de l'inclinaison de l'axe de rotation terrestre par rapport à l'écliptique et au plan orbital de la lune, les forces de marée exercent sur ce renflement un couple de forces responsable du phénomène appelé précession des équinoxes.

Dissipation de marée

Dans le cas du système Terre-Lune, les "bosses de marée" sont, à cause de leur inertie, en quelque sorte "entraînées" par le mouvement de rotation de la Terre sur elle-même. Il en résulte deux couples de forces. L'un freine la rotation de la Terre sur elle-même. Son travail est dissipé sous forme de chaleur principalement. L' autre accroît la distance Terre-Lune. Son travail est conservé sous forme d'énergie potentielle de gravitation. Actuellement et en moyenne, la puissance totale de la dissipation de marée, due principalement à la Lune et au Soleil, est sur Terre de 3,75 Terawatts ; le ralentissement du jour terrestre est de 2,3 ms/siècle et l'éloignement de la Lune de 3,84 cm/an.

Traitement mathématique

Étant donné un champ gravitationnel extérieur donné, l'accélération de marée à un point d'un corps est obtenue par soustraction vectorielle de l'accélération au centre du corps de celle au point. La force de marée est la force qui correspond à cette accélération. Il est à noter que la seule force de gravitation tenue en compte pour ces calculs est celle entre les deux corps, donc la force extérieure ; le champ gravitationnel du corps lui-même n'est pas pertinent.

L'accélération de marée ne requiert pas de rotation ou que le corps soit en orbite. Par exemple, le corps peut être en chute libre en ligne droite, sous l'influence d'un champ gravitationnel et quand même être soumis à une accélération de marée (de plus, cette accélération varie elle-même).

Application de la loi universelle de la gravitation

Le champ de gravité généré par un deuxième corps situé à droite de la sphère noire ; au-dessus, le champ de gravité ; au-dessous, le résultat de la soustraction algébrique du champ moyen. À droite, la matière de surface est plus tirée vers le haut ; à gauche, elle est moins tirée, mais vers le "bas" : il y a donc "allègement" dans les deux cas.

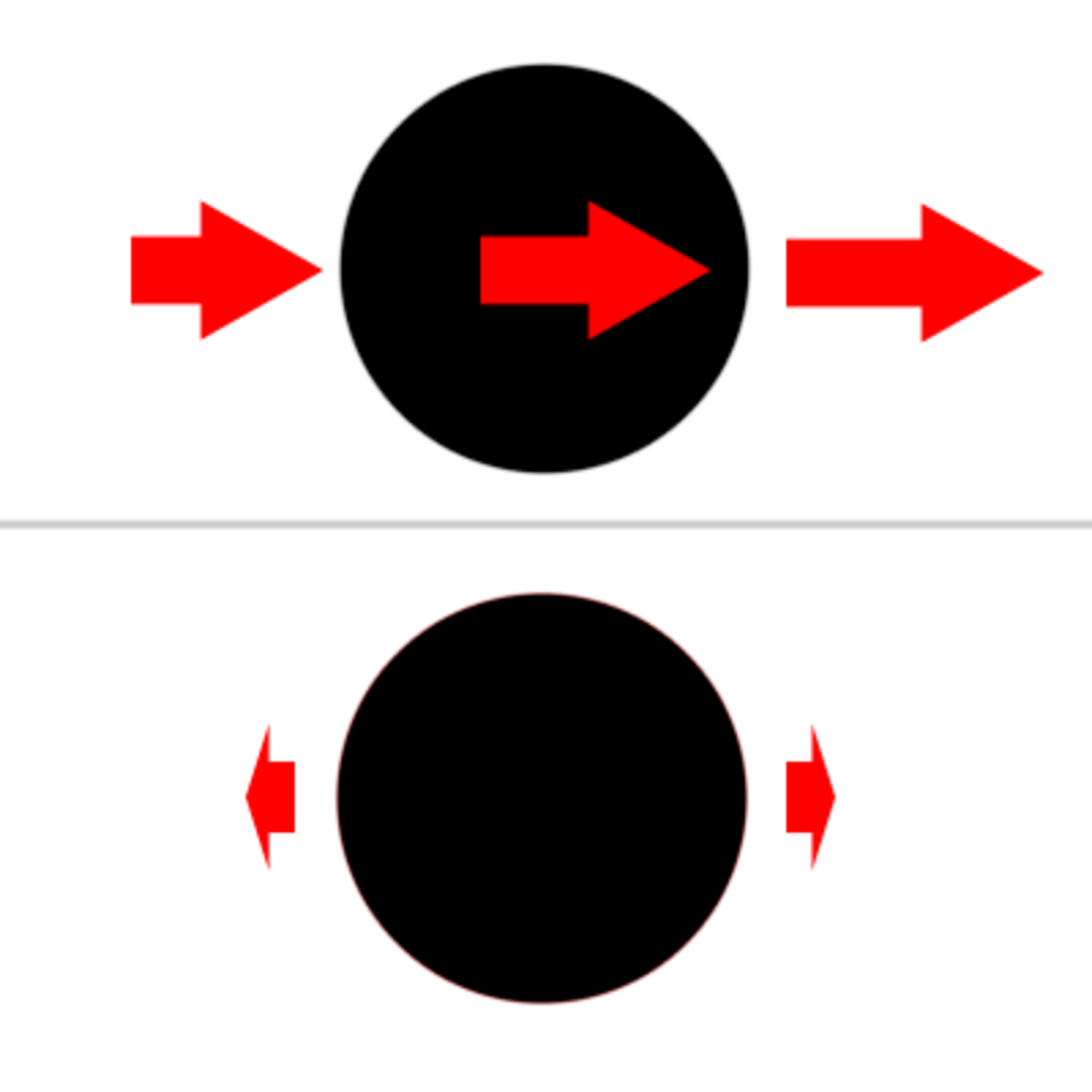
Selon la loi universelle de la gravitation, une particule de masse m à une distance r du centre d'une sphere de masse M subit une force égale à :

,

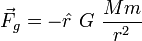
où est le vecteur unitaire qui pointe dans la direction qui va à partir de M jusqu'à la particule m.

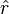
On étend la description de m pour qu'il représente un petit corps sphérique avec un volume donné. Posons R, la distance inter-objet, c'est-à-dire du centre de M à celui de m et posons ∆r, le rayon de m. Par conséquent, les points sur la surface de m sont situés à une distance r = R ± ∆r du centre de R. On applique alors l'équation ci-haut et, en ignorant la contribution négligeable du la masse de m au champ gravitationnel, on obtient la force gravitationnelle en ces points :

Application de la série de Taylor

Le développement de 1/(1 + x)² par la série de Taylor est 1 – 2x + 3x² – ... Donc, on met en évidence le R du dénominateur pour obtenir :

et on applique le développement en série au résultat :

Le premier terme de la série est la force gravitationnelle telle qu'on la connaît traditionnellement. En général, le deuxième terme est beaucoup plus significatif que les suivants. Par conséquent, la force de marée s'exprime comme :

où dans F_t, l'indice t rappelle tide, ou marée en anglais.