Infini - Définition

En théologie

En Inde, dès l'antiquité, la religion jaïniste considérait le monde comme infini.

Les religions monothéistes induisent généralement la notion d'infinité (ou plus précisément les notions d'éternité et de transcendance), même si elle est moins formalisée que la notion mathématique correspondante.

Une des premières manifestations de cette notion remonte à l'Égypte ancienne, au temps d'Akhénaton, autour du culte du dieu Aton.

Depuis les années cinquante les toitures de certaines églises modernes sont en forme de paraboloïde hyperbolique de sorte que leurs lignes semblent converger vers un point à l'infini. C'est le cas de l'église Saint-Thibaut au Pecq. Dans la plaquette éditée par "l'association des Amis de Saint Thibaut" en mai 1965 un chapitre s'intitule: "Que tout s'élève vers l'infini" il y est écrit: "...L'arêtier-poursuit l'exposé du parti-est une hyperbole et nous avons déterminé cette courbe de sorte que l'assemblée ne puisse en voir l'extrémité. Nous pensons que cette particularité contribuera à suggérer l'élan vers l'infini. Telles étaient les idées des architectes" et on lit en légende du tracé schématique de la toiture: "Tracé schématique de la forme de l'église, montrant comment on a pu construire les paraboloïdes hyperboliques à partir d'éléments rectilignes. Les quatre voiles de bois se rejoignent à leur pointe, déterminant une convergence vers l'infini....

Dans les exemples qui précèdent, l'idée de transcendance est associée à une notion d'espace ou de temps infini. A l'époque moderne Cantor l'associa aussi, semble-t-il, à l'infinité numérique, considérant que ses travaux sur les nombres cardinaux et ordinaux avaient des implications théologiques.

En physique

Au début du XX^e siècle, la physique se trouvait dans l'impossibilité d'expliquer divers phénomènes, dont le fait qu'un corps noir à l'équilibre thermodynamique est censé rayonner un flux infini (voir catastrophe ultraviolette). Ce problème fut résolu par l'introduction des quanta par Planck, ce qui forme la base de la physique quantique.

Dans le cadre de la relativité générale, le Big Bang conduit, dans son interprétation naïve, à l'apparition de valeurs infinies (on parle aussi de singularités) à l'origine des temps, apportant ainsi la preuve que nos connaissances physiques actuelles ne sont pas capables de décrire cette époque lointaine de l'histoire de l'Univers.

Dans plusieurs branches de la physique, comme la théorie quantique des champs ou la physique statistique, les chercheurs ont pu éliminer les divergences indésirables de la théorie à l'aide de techniques mathématiques de renormalisation. Ces techniques n'ont pu être appliquées pour l'instant à la théorie de la gravitation.

Histoire

Usage et opérabilité des quantités infinies

L'infini potentiel chez les anciens

Les mathématiciens ont de tout temps utilisé l'appartenance et l'inclusion mais ont eu les plus grandes difficultés à formuler au moyen de ces relations des théorèmes sur les nombres et les grandeurs. C'est ainsi qu'Euclide, au lieu de dire « l'ensemble des nombres premiers est infini », dit « pour toute quantité donnée de nombres premiers, il y en a un plus grand ». De même, Aristote se refuse à considérer qu'une ligne droite est « composée de points ».

Galilée remarque qu'il y a une correspondance biunivoque entre les nombres et leurs carrés, d'où il déduit que l'assertion commune « le tout est plus grand que la partie » ne se vérifie pas lorsqu'on parle de quantités infinies. Cependant, loin d'y trouver une motivation pour l'étude des ensembles infinis, il y voit la preuve du caractère non opérationnel de tels ensembles, position approuvée plus de deux siècles plus tard par Cauchy. Ainsi donc, jusqu'assez avant dans l'époque moderne, les mathématiciens s'interdisaient d' utiliser directement les ensembles infinis et préféraient raisonner « en compréhension » sur les propriétés de leurs éléments. Ils se contentaient alors de la possibilité d'augmenter toute grandeur donnée, ou de la diminuer s'il s'agit d'une grandeur continue.

Ceci n'empêcha pas la naissance du calcul infinitésimal, ainsi la phrase « pour tout ε>0 il existe n₀ tel que n≥n₀ implique |u_n - L| < ε » s'abrège en ou «  u_n tend vers L quand n tend vers l'infini », donc, ainsi que le reconnaît Bourbaki, cette position avait permis des développements importants tout en posant des garde-fous.

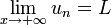
L'infini potentiel chez les constructivistes modernes

Issu de la « crise des fondements » du début du XX^e siècle, le courant intuitionniste promu par Brouwer, rejette les méthodes de la logique classique, censée ne pas s'appliquer en tout cas aux objets infinis. Aujourd'hui ce terme d'intuitionniste s'applique à une axiomatisation bien précise de la logique sans tiers exclu. Une forme de philosophie mathématique qui se revendique volontiers de celle de Brouwer est celle du courant constructiviste, dont un représentant notoire, Roger Apéry a ainsi exposé la conception de l'infini :

S'il extrapole la réalité, le mathématicien constructif refuse les hypothèses fantastiques des platoniciens ; en effet (......) il constate que la mathématique se déroule dans le temps. (.......) son immortalité lui permet d'atteindre des nombres aussi grands qu'il veut, mais pas de définir tous les nombres ; il croit à l'infini potentiel, pas à l'infini actuel.

On voit d'après ce texte que pour les constructivistes, contrairement au point de vue majoritaire qui considère des ensembles dont les parties sont données simultanément, les mathématiques ont pour objet des processus, dont les étapes se construisent séquentiellement ; car pour eux il s'agit bien d'une activité humaine ; « il n'y a pas de mathématiques sans mathématicien » dit Apéry.

L'infini actuel et le temps

Au Moyen Âge, saint Bonaventure avait affirmé que d'un pur point de vue logique — indépendamment de ce que disait la Bible — il était impossible que le monde ait toujours existé ; Thomas d'Aquin réfuta cette assertion par un raisonnement formel, rien en l'absence d'information ne permettant d'exclure a priori une éternité actuellement achevée.

Un sophisme célèbre, imaginé par le créationniste américain W.L. Craig d'après une parabole de Bertrand Russell dont le but était autre, prétend démontrer l'impossibilité d'une durée infinie achevée, et donc prouver que le monde a eu un commencement, par l'histoire de Tristram Shandy, lequel écrit son autobiographie au rythme d'un an d'écriture par journée vécue, et a fait cela toutes les années du passé. Si donc le temps n'a jamais commencé, quel jour de sa vie Tristram Shandy est-il en train de commenter cette année ? Aucun jour du passé ne conviendrait, donc il est impossible que le temps n'ait pas une origine.

La supercherie est évidente pour qui connaît les coordonnées cartésiennes et les histoires de trains qui se rattrapent: le scénario comporte une contradiction ; Tristram Shandy qui écrit 365,25 fois moins vite que l'horloge a nécessairement commencé son autobiographie quelque jour, ce qui invalide l'argument.

Dans l'imagerie populaire

Dans l'expression populaire, l'adjectif « infinies » est parfois employé pour qualifier de très vastes étendues ou de très grandes quantités.

Remarquons que même finis, les très grands nombres peuvent être difficiles à concevoir. Ainsi les suites de Goodstein sont des suites définies très simplement qui donnent lieu à des nombres qui dépassent l'entendement, bien qu'ils soient encore considérablement plus petits que ceux engendrés par le castor affairé.

Certains auteurs modernes se sont inspirés du passage biblique de la Tour de Babel pour assimiler « le ciel » à un but infiniment éloigné..

Les notations

Le symbole ∝ qui revient fréquemment en analyse a été employé pour la première fois en 1655 par John Wallis, dans son ouvrage De sectionibus conicis, puis peu après dans l'Arithmetica Infinitorum :

esto enim ∞ nota numeri infiniti.

Trois hypothèses existent quant à l'origine de ce choix. La plus communément admise est qu'il s'agit d'une évolution du chiffre désignant '1000' dans la numération romaine : successivement Ⓧ, puis CIƆ, avant de devenir M. L'évolution graphique du deuxième symbole aurait donné . Parallèlement on note l'emploi du mot latin mille au pluriel pour désigner un nombre arbitrairement grand et inconnu. On notera l’expression française encore utilisée aujourd’hui « des mille et des cents » rappelant cet usage. Le symbole actuel serait donc simplement l’évolution de la ligature minuscule cıɔ en écriture manuscrite onciale.

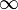
Une hypothèse concurrente est que le symbole serait issu de la lettre grecque ω, dernière lettre de l'alphabet grec, et métaphore courante pour désigner l'extrémité finale (comme dans l'expression l'alpha et l'oméga). Depuis Georg Cantor on utilise d'ailleurs des lettres grecques pour désigner les nombres ordinaux infinis. Le plus petit ordinal infini, qui correspond au bon ordre usuel sur les entiers naturels, est noté ω.

Enfin, Georges Ifrah, dans son encyclopédie « L'histoire universelle des chiffres », explique que la graphie de l'infini remonte à la civilisation indienne, et plus particulièrement à la mythologie indienne. L'Ananta, (terme sanskrit qui signifie infini) le « serpent infini » du dieu Vishnu, est représenté enroulé sur lui-même à la manière d'un « huit renversé ».