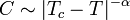Transition de phase - Définition
En physique, une transition de phase est une transformation du système étudié provoquée par la variation d'un paramètre extérieur particulier (température, champ magnétique...).
Cette transition a lieu lorsque le paramètre atteint une valeur seuil (plancher ou plafond selon le sens de variation). La transformation est un changement des propriétés du système ; cela peut être :
- la transformation d'un système thermodynamique d'une phase à une autre : fusion, ébullition, sublimation...
- le changement de comportement magnétique d'une pièce metallique ou céramique :
- un métal ferromagnétique passe d'un comportement paramagnétique à diamagnétique au point de Curie ;
- certaines céramiques deviennent supraconductrices en dessous d'une température critique,
- la condensation quantique de fluides bosoniques en condensat de Bose-Einstein ;
- la disparition de symétrie dans les lois de la physique au début de l'Histoire de l'univers quand sa température refroidit.
Les transitions de phases ont lieu lorsque l'énergie libre d'un système n'est pas une fonction analytique (par exemple non-continue ou non-dérivable) pour certaines variables thermodynamiques. Cette non-analyticité provient du fait qu'un nombre extrêmement grand de particules interagissent ; ceci n'apparaît pas lorsque les systèmes sont trop petits.
Types de transition de phase courants
Voici le nom des transitions de phases les plus courantes qui font intervenir les états de la matière suivants : solide, liquide, gazeux :
- de solide à liquide : fusion
- de solide à gazeux : sublimation
- de liquide à solide : solidification
- de liquide à gazeux : évaporation ou ébullition ou vaporisation
- de gazeux à solide : déposition ou condensation
- de gazeux à liquide : condensation ou liquéfaction.
| De ↓ à → | solide | liquide | gazeux |
| solide | X | fusion | sublimation |
| liquide | solidification | X | évaporation ou vaporisation ou ébullition |
| gazeux | déposition ou condensation | condensation ou liquéfaction | X |
Classification des transitions de phase
Classification d'Ehrenfest
Paul Ehrenfest tenta le premier de classifier les transitions de phase, en se basant sur le degré de non-analyticité. Bien qu'utile, ce classement n'est qu'empirique et ne représente pas la réalité des mécanismes de transition.
Cette classification se base sur l'étude de la continuité des dérivées ne de l'énergie libre :
Les transitions du premier ordre sont celles pour lesquelles la dérivée première selon une des variables thermodynamiques de l'énergie libre est discontinue (présence d'un "saut" dans cette dérivée). Par exemple, les transitions solide/liquide/gaz sont de premier ordre : la dérivée de l'énergie libre selon le volume donne la pression, et celle-ci change de manière discontinue lors des transitions.
Les transitions du deuxième ordre sont celles pour lesquelles la dérivée seconde selon une des variables thermodynamiques de l'énergie libre n'est pas continue. Elles comprennent la transition ferromagnétique dans des matières comme le fer : la dérivée première de l'énergie libre selon le champ magnétique appliqué est l'aimantation, la dérivée seconde est la susceptibilité magnétique et celle-ci change de manière discontinue à la température dite " de Curie " (ou point de Curie).
Classification actuelle des transitions de phase
La classification d'Ehrenfest a été abandonnée car elle ne prévoyait pas la possibilité de divergence - et pas seulement de discontinuité - d'une dérivée de l'énergie libre. Or, de nombreux modèles, dans la limite thermodynamique, prévoient une telle divergence[1]. Ainsi, par exemple, la transition ferromagnétique est caractérisée par une divergence de la capacité calorifique (dérivée seconde de l'énergie libre).
La classification utilisée actuellement distingue également des transitions de premier et de second ordre, mais la définition est différente.
Les transitions de premier ordre sont celles qui impliquent une chaleur latente. Au cours de ces transitions, le système absorbe ou émet une quantité d'énergie fixe (et en général grande). Comme l'énergie ne peut pas être transférée instantanément entre le système et son environnement, les transitions de premier ordre ont lieu dans des phases étendues dans lesquelles toutes les parties ne subissent pas la transition au même moment ; ces systèmes sont hétérogènes. C'est ce que l'on constate lors de l'ébullition d'une casserole d'eau : l'eau n'est pas instantanément transformée en gaz mais forme un mélange turbulent d'eau et de bulles de vapeur d'eau. Les systèmes étendus hétérogènes sont difficiles à étudier car leurs dynamiques sont violentes et peu contrôlables. C'est le cas de nombreux systèmes, et notamment des transitions solide/liquide/gaz.
Les transitions de second ordre sont des transitions dites " de phase continues " ; il n'y a pas de chaleur latente associée. C'est le cas par exemple de la transition ferromagnétique, de la transition superfluide et de la condensation de Bose-Einstein.
Il existe également des transitions de phase d'ordre infini. Elles sont continues mais ne brisent aucune symétrie (voir ci-dessous). L'exemple le plus fameux est la transition Berezinsky-Kosterlitz-Thouless dans le modèle XY à deux dimensions. Ce modèle permet de décrire de nombreuses transitions de phase quantiques dans un gaz d'électrons à deux dimensions.
Propriétés des transitions de phase
Points critiques
Dans le cas de la transition entre les phases liquide et gaz, il existe des conditions de pression et de température pour lesquelles la transition entre le liquide et le gaz devient du second ordre. Près de ce point critique, le fluide est suffisamment chaud et comprimé pour que l'on ne puisse pas distinguer les phases liquides et gazeuses.
Le système a une apparence laiteuse en raison des fluctuations de la densité du milieu, qui perturbe la lumière sur tout le spectre visible. Ce phénomène est appelé opalescence critique.
On retrouve également ce type de transition dans les systèmes magnétiques.
Symétrie
Les phases avant et après transition ont souvent, mais pas systématiquement, des symétries différentes.
Considérons par exemple la transition entre un fluide (liquide ou gaz) et un solide cristallin. Le fluide est composé de molécules arrangées de manière désordonnée mais homogène, il possède une symétrie translationnelle continue : chaque point dans le fluide a les même propriétés que n'importe quel autre point. Le solide cristallin par contre est fait d'atomes arrangés selon un réseau. Ce réseau est hétérogène et anisotrope : les propriétés varient grandement d'un point à un autre, et selon les directions considérées, mais sont périodiques.
La transition ferromagnétique est un autre exemple d'une transition brisant la symétrie ; il s'agit dans ce cas de la symétrie des courants électriques et des lignes de champ magnétique. Cette symétrie est brisée par la formation de domaines magnétiques contenant des moments magnétiques alignés. Chaque domaine a un champ magnétique pointant dans une direction fixée choisie spontanément pendant la transition de phase. On parle de " symétrie de haut et bas ", ou de " symétrie d'inversion du temps " car les courants électriques inversent leur direction quand le sens du temps est inversé.
La présence ou l'absence d'une rupture de symétrie est importante pour le comportement des transitions de phase. Ceci fut noté par Landau : il n'est pas possible de trouver une fonction continue et dérivable entre des phases possédant une symétrie différente. Ceci explique qu'il n'est pas possible d'avoir un point critique pour une transition solide cristallin-fluide. Les transitions brisant une symétrie sont nécessairement du premier ou du second ordre.
En général, la phase la plus symétrique est la phase stable à haute température ; c'est par exemple le cas des transitions solide-liquide et ferromagnétique. En effet, l'Hamiltonien d'un système présente habituellement toutes les symétries possibles du système, et certaines de ces symétries sont absentes dans les états de basse énergie ; on appelle ceci la rupture spontanée de symétrie.
La rupture de la symétrie nécessite l'introduction de variables supplémentaires pour décrire l'état du système. Par exemple dans la phase ferromagnétique, il faut pour décrire le système indiquer l'" aimantation nette " des domaines qui s'opère lors du passage sous le point de Curie. Ces variables sont des paramètres d'ordre. Notez cependant que les paramètres d'ordre peuvent aussi être définis pour des transitions qui ne rompent pas la symétrie.
Les transitions de phase qui brisent la symétrie jouent un rôle important en cosmologie. Dans la théorie du Big bang, le vide (théorie du champ quantique) initial possède un grand nombre de symétries. Au cours de l'expansion de l'univers, le vide se refroidit ce qui entraîne une série de transitions brisant des symétries. Par exemple, la transition électro-faible rompt la symétrie SU(2)×U(1) du champ électrofaible, le champ électromagnétique actuel ayant une symétrie U(1). Cette transition est importante pour comprendre l'asymétrie entre la quantité de matière et d'antimatière dans l'univers présent (voir baryogénèse électrofaible).
Exposants critiques et classes d'universalité
Les transitions de phase continues sont plus faciles à étudier que celles de premier ordre en raison de l'absence de chaleur latente, et elles ont de nombreuses propriétés intéressantes. Le phénomène associé avec la transition de phase continue est appelé phénomène critique, en raison de son association avec les points critiques.
Les transitions de phase continues peuvent être caractérisées par des paramètres appelés exposants critiques. Bien que la transition soit continue (et donc ne se fasse pas à température constante), on peut tout de même définir une température critique Tc.
Quand T est proche Tc, la capacité calorifique C suit typiquement une de loi de puissance :
La constante α est l'exposant critique associé avec la capacité calorifique. Puisque la transition n'a pas de chaleur latente, il faut nécessairement que α soit strictement inférieur à 1 (sinon, la loi C(T) n'est plus continue). La valeur de α dépend du type de transition de phase considéré :
- pour -1 < α < 0, la capacité calorifique a une " anomalie " à la température de transition. C'est le comportement de l'hélium liquide à la " transition lambda " d'un état " normal " vers l'état superfluide ; expérimentalement, on trouve α = -0,013±0,003 dans ce cas.
- Pour 0 < α < 1, la capacité calorifique diverge à la température de transition, cependant, la divergence n'est pas assez importante pour produire une chaleur latente. La troisième dimension de la transition de la phase ferromagnétique suit un tel comportement. Dans le modèle Ising tri-dimensionel pour les aimants uniaxiaux, des études théoriques détaillées ont déterminé une valeur de l'exposant α ∼ 0,110.
Quelques systèmes ne suivent pas cette loi de puissance. Par exemple, la théorie de champ moyen prédit une discontinuité finie de la capacité calorifique à la température de transition, et le modèle Ising bi-dimensionel a une divergence logarithmique. Cependant, ces systèmes sont des modèles théoriques, ; les transitions de phase observées jusqu'ici suivent toutes une loi de puissance.
On peut définir plusieurs exposants critiques - notés β, γ, δ, ν, et η - correspondant aux variations de plusieurs paramètres physiques autour du point critique.
Fait remarquable, des systèmes différents possèdent souvent le même ensemble d'exposants critiques. Ce phénomène est appelé universalité. Par exemple, dans le cas du point critique liquide-gaz, les exposants critiques sont largement indépendants de la composition chimique du fluide. Plus surprenant, les exposants critiques de la transition de phase ferromagnétique sont exactement les mêmes pour tous les aimants uniaxiaux. De tels systèmes sont dits être dans la même classe d'universalité.
L'universalité est une prédiction de la théorie de la transition de phase du groupe de renormalisation, qui indique que les propriétés thermodynamiques d'un système près de la transition dépend seulement d'un petit nombre d'éléments, comme la dimensionalité et la symétrie, et est insensible aux propriétés sous-jacentes microscopiques du système.
Notes
- ↑ Les divergences ne peuvent apparaitre que dans la limite thermodynamique, c'est-à-dire lorsque l'on fait croitre la taille du système vers l'infini. En effet, un système de taille finie est décrit par une fonction de partition qui est une somme finie d'exponentielles, et qui est donc analytique pour toute température.