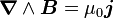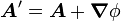Champ magnétique - Définition
La liste des auteurs de cet article est disponible ici.
Calcul du champ magnétique
Propriétés mathématiques
Symétries
En tant que champ pseudovectoriel, le champ magnétique a un comportement particulier par rapport aux symétries. En effet, contrairement au champ (vectoriel) électrique, les champs magnétiques ne suivent pas la symétrie de leurs sources. On parle ainsi de vecteur « axial » ou de « pseudovecteur ».
Par exemple, pour une spire circulaire parcourue par un courant :
- un plan de symétrie Π+ est celui qui contient la spire ;
- un plan d'antisymétrie Π- est tout plan passant par le centre de la spire et orthogonal au premier plan.
Respectivement, Π+ et Π- sont un plan d'antisymétrie et de symétrie pour le champ magnétique.
Changement de référentiel
En mécanique classique, où l'on considère des vitesses relatives très inférieures à la vitesse de la lumière, le champ magnétique mesuré est identique dans deux systèmes de coordonnées en translation rectiligne et uniforme l'un par rapport à l'autre (référentiels galiléens). Cette propriété n'est pas partagée par le champ électrique, dont la valeur change d'un référentiel à l'autre si le champ magnétique est non nul.
Calcul du champ
Le calcul du champ magnétique créé par un système demande de résoudre des équations différentielles assez complexes. Il existe pour cela une multitude de méthodes numériques comme la méthode des éléments finis, la méthode des différences finies et la méthode des volumes finis pour ne citer que les méthodes les plus répandues. Toutefois, il est possible de calculer analytiquement le champ magnétique dans certains cas simples. Sauf mention contraire, les expressions données pour le calcul du champ magnétique sont exprimées dans les unités SI. Cela explique notamment le facteur 1/4 π.
Théorème d'Ampère
À partir des observations révélant un lien entre courants électriques et champ magnétique, André-Marie Ampère énonça une loi d'abord phénoménologique, qui décrivait l'effet observé. Démontrée depuis, dans le cadre plus général de l'électromagnétisme, cette relation est devenue le théorème d'Ampère. Elle n'est valable, en toute rigueur, que dans les cas magnétostatiques.
La formulation originelle de ce théorème est la suivante :
-
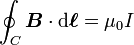
B étant le champ magnétique, C une courbe fermée et orientée et I l'intensité qui traverse une surface délimitée par C.
Cete équation peut être écrite localement, on a alors :
où μ est la perméabilité magnétique du vide, et j le vecteur densité de courant.
Cette relation étant mise en défaut dans le cas de champs magnétiques ou électriques dépendant du temps, Maxwell introduisit en 1861 les « courants de déplacement », dont la variation corrigeait cette relation : c'est l'équation locale de Maxwell-Ampère. On peut l'écrire localement sous la forme :
-
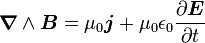
E étant le champ électrique et ε la perméabilité électrique du vide.
On peut a posteriori réécrire cette loi sous forme intégrale, également appelée théorème d'Ampère :
-
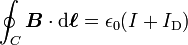
avec
-
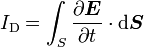
où S est la surface délimitée par le contour C.
Ceci se comprend aisément grâce au théorème de Green-Stokes :
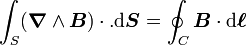
Loi de Biot-Savart locale
La loi de Biot-Savart permet de donner l'expression du champ magnétique dans un milieu de perméabilité magnétique isotrope et homogène.
Le champ B généré en un point de coordonnées r par une charge q en mouvement, située en un point r’ et se déplaçant à la vitesse v, est donné par la relation suivante :
-
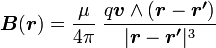
Loi de Biot-Savart intégrale
Si on a affaire à une distribution de courants, qui est connue en tout point, alors on peut intégrer la relation locale.
Avec les notations précédentes, cela donne :
-
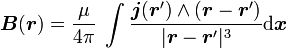
Potentiel vecteur
L'absence de monopôles magnétique implique que la divergence du champ magnétique est nulle :
-
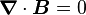
Ceci implique, d'après les théorèmes de l'analyse vectorielle, qu'il existe un champ vectoriel A, dont le rotationnel est égal à B :
-

Un tel champ A est appelé potentiel vecteur, par analogie au potentiel électrique, dit « potentiel scalaire », du champ électrique.
Ce potentiel n'est toutefois pas unique : il est défini à un gradient près. En effet, le rotationnel d'un gradient est identiquement nul, aussi le potentiel vecteur A’ défini par :
vérifie-t-il également la relation :
-

De façon quelque peu étrange, la quantité fondamentale n'est pas le champ magnétique mais le potentiel vecteur, alors que ce dernier ne peut être défini de façon univoque. Une telle situation est appelée en physique invariance de jauge : des phénomènes identiques, ici le champ B, peuvent être générés par plusieurs configurations, appelées pour diverses raisons historiques « jauges » de l'objet fondamental, ici le champ A. D'un point de vue mathématique, l'invariance de jauge est la cause d'une loi fondamentale de l'électromagnétisme, la conservation de la charge électrique. Cette loi, expérimentalement vérifiée à une très grande précision implique en effet que l'objet fondamental apparaissant en électromagnétisme n'est ni le champ magnétique ni le champ électrique, mais le potentiel vecteur et le potentiel électrique.
Connaissant A, on peut facilement en déduire B. Le fait que le potentiel vecteur soit plus fondamental que le champ magnétique transparaît en mécanique quantique, où en présence de champ magnétique, c'est en fait le potentiel vecteur qui apparaît dans l'équation de Schrödinger, qui décrit l'évolution des particules élémentaires. L'illustration la plus manifeste de la prééminence du potentiel vecteur se trouve dans l'effet Aharonov-Bohm, où l'on est amené à considérer des configurations dans lesquelles le champ B s'annule dans certaines régions alors que le potentiel vecteur A n'est pas nul (mis de rotationnel nul) et influence explicitement le comportement des particules.
Il est d'ailleurs possible de calculer le potentiel vecteur A directement à partir de la donnée des courants :
-
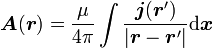
l'expression ci-dessus n'étant valable que lorsque les courants — donc les champs — ne dépendent pas du temps. En pratique, ces variations peuvent souvent être négligées tant que l'on n'étudie pas les ondes et leur propagation.
Dans ces derniers cas, il faut remplacer l'expression ci-dessus par une expression plus complexe, faisant appel au concept de potentiels retardés pour tenir compte du temps de propagation du champ magnétique.