Héron d'Alexandrie - Définition

Introduction

Héron d'Alexandrie
Naissance	Ier siècle ap. J.C. Alexandrie (Égypte)
Domicile	Alexandrie
Champs	Mathématiques, mécanique
Célèbre pour	Éolipyle, Formule de Héron
modifier

Héron d'Alexandrie ou Héron l'Ancien (Ἥρων ὁ Ἀλεξανδρεύς) est un ingénieur, un mécanicien et un mathématicien grec du I^er siècle après J.-C.

Présentation

De la vie de Héron, on ne sait pas grand chose, si ce n'est qu'il est originaire d'Alexandrie. C'est si vrai que les historiens se sont longtemps divisés sur l'époque où il a vécu. Leurs estimations allaient du IIe siècle avant J.-C. au IIIe siècle de notre ère. Aujourd'hui, la querelle est éteinte : Philippe Fleury montre clairement que Héron est postérieur à Vitruve, mort en -20, et Gilbert Argoud qu'il fut contemporain de Pline l'Ancien (23-79) et actif autour de l'an 62. Il a donc bien vécu au premier siècle après J.-C. et sans doute au début du IIe siècle, donc sous l'Empire romain, mais dans la très grecque Alexandrie.

Héron d’Alexandrie crée des automates mus par l’eau, s’intéresse à la vapeur et à l’air comprimé. Principalement connu pour les machineries décrites dans son Traité des pneumatiques ( Πνευματικά), on lui doit par exemple un projet de machine destinée à ouvrir automatiquement les portes d’un temple.

Son œuvre nous fut transmise via quelques-uns de ses traités de physique et de mathématiques. Nombre de ses écrits ont été retrouvés, traduits en latin et en arabe. Au cours des siècles, ils ont été maintes fois retraduits et retranscrits et, pour certains d'entre eux, leur paternité est parfois mise en cause.

Publications

La paternité de Héron n'est pas sûre pour les ouvrages marqués d'une astérisque.

• Πνευματικά (Pneumatica) : Deux livres sur la pression de l'air et de la vapeur d'eau.
• Μηχανική (Mechanikè) : Trois livres sur les moyens de soulever des objets et sur leur centre de gravité.
• Μετρική (Metrikè) : Trois livres sur les différents moyens de mesurer.
• Γεομετρικά (Geometrica) * : Illustration par des exemples des théories développées dans Métrikè.
• Κατοπτρικά (Catoptrica) : Les miroirs.
• Στερεομετρικά (Stereometrica) * : Recueil de problèmes.
• Βελοποικά (Belopoica) : Les machines de jet.
• Αυτόματα (Automata) : Les automates.
• Περὶ διόπτρας (Peri dioptras) : Étude sur les dioptres, sortes de théodolites.
• Mensurae * : Instruments de mesure.
• Χειροβάλιστρα (Cheirobalistra) *: Catapultes.
• Definitiones * : Définitions mathématiques.
• Γεωδεσία (Geodesia) : (fragments)
• Geoponica : (fragments)

Réalisations

Mathématiques

On attribue à Héron d'Alexandrie plusieurs formules mathématiques dont une méthode de calcul de l'aire d'un triangle sans utiliser de hauteur (formule de Héron), ainsi qu'une autre permettant d'approcher la racine carrée de n'importe quel nombre de manière récursive (Méthode de Héron). Cependant, la première formule est déjà prouvée par Archimède, et la seconde est déjà connue des Babyloniens.

Il fut aussi dans Stereometrica, l'auteur de formules de mesures de longueur, de surface et de volume pour des objets en trois dimensions. Les recherches mathématiques de Héron d'Alexandrie visaient principalement l'aspect pratique de la mesure des objets.

Formule de Héron

Cette formule permet de calculer l'aire d'un triangle en connaissant la longueur de ses côtés, sans utiliser la hauteur.

Soit ABC un triangle quelconque ayant pour longueurs des côtés a, b et c.

Avec le demi-périmètre ,

l'aire du triangle est :

Démonstration

La démonstration de Héron d'Alexandrie s'appuie sur une démarche géométrique en 5 propositions :

Proposition 1 : Les bissectrices des angles d’un triangle se rencontrent en un point qui est le centre du cercle inscrit dans ce triangle.

Proposition 2 : Dans un triangle rectangle, la hauteur issue de l’angle droit est moyenne proportionnelle entre les deux segments qu’elle détermine sur l’hypoténuse.

Proposition 3 : Dans un triangle rectangle, le milieu de l’hypoténuse est équidistant des trois sommets.

Proposition 4 : Si ABCD est un quadrilatère avec diagonales et que ∠DBC et ∠DAC sont droits, alors il est possible de tracer un cercle passant par A, B, C et D.

Proposition 5 : Les angles opposés d’un quadrilatère inscrit dans un cercle sont supplémentaires (équivalents à deux angles droits).

Optique

Héron l'Ancien étudie dans Catoptrica la lumière et ses réflexions. Il énonce ainsi les principes de réflexion de la lumière, principes guidés par la règle selon laquelle la nature choisit toujours le chemin le plus court . Il croyait à l'époque que la vision était possible grâce à des rayons lumineux émis par les yeux et se propageant à une vitesse infinie.

Mécanique et pneumatique

Héron imagine des mécaniques assez curieuses, mais assez complexes, comme un distributeur automatique (payant) d'eau pour les libations ou une machine à rendre les oracles, qui est en fait une escroquerie. Mais son but n'est pas vénal. Il est mû par l'envie de trouver sans cesse de nouvelles machines et des applications de ses recherches et par le plaisir d'étonner ses contemporains..

Éolipyle

Héron d'Alexandrie a conçu de nombreuses machines hydrauliques. Il est à l'origine de l'éolipyle (porte d'Eole), machine pneumatique constituée d’une sphère fixée sur un axe et équipée de deux tubes coudés sortant de manière opposée. En chauffant l'eau contenue dans la chaudière inférieure, la vapeur d'eau formée donne en s’échappant un mouvement de rotation à la sphère. En effet, de cette chaudière sort un tube creux relié à une sphère pouvant tourner autour d'un axe horizontal et comportant deux autres petits tubes perpendiculaires à l'axe laissant sortir la vapeur qui fait tourner la sphère.

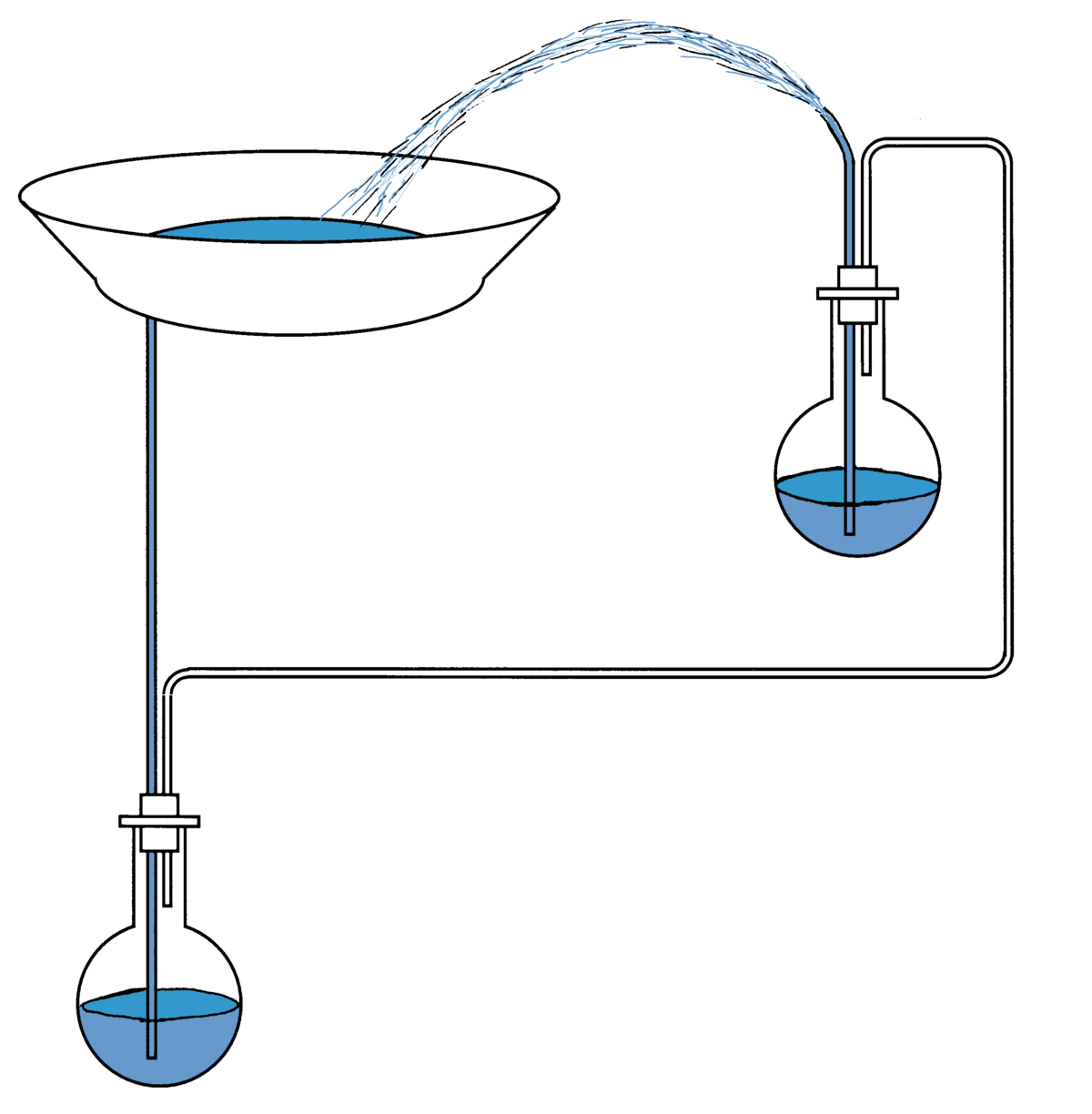
Fontaine

La « fontaine de Héron », décrite dans les Pneumatica

Il a aussi conçu une fontaine automatique qui faisait jaillir l'eau via un ingénieux système de vases communicants. Dans Pneumatica il décrit un système de portes automatiques s'ouvrant lorsqu'on allume un feu sur un autel ; le feu, chauffant un volume d'eau, créait de la vapeur qui mettait en mouvement les portes d’un temple.

Dans le cadre de son Traité des automates il a aussi conçu des mécanismes pour théâtre à base de poids et contrepoids mettant en mouvement une série de plates-formes et de petits personnages.

Grâce à ces inventions, Héron d'Alexandrie est souvent retenu comme l'inventeur des premiers automates. Mais c'est sans doute à tort, puisqu'il fut manifestement précédé par Philon de Byzance et Ctésibios.

Autres

Héron l'Ancien fut aussi l'inventeur d'un pseudo-thermomètre et de l'odomètre permettant de mesurer la distance parcourue. On lui attribue la fabrication d’une clepsydre pour mesurer le temps, et la réalisation d'ouvrages sur l'astrolabe permettant de mesurer la distance angulaire entre deux astres.