Propriétés du potentiel newtonien - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Cet article fort technique traitant en détail des propriétés d'un potentiel inversement proportionnel à la distance s'adresse avant tout aux étudiants et aux chercheurs en géodésie physique et en géophysique, mais peut aussi intéresser les physiciens théoriciens. Sa lecture demande une tournure d'esprit orientée vers les mathématiques appliquées.
Potentiel gravitationnel et force de gravitation
On appelle le potentiel gravitationnel d'une masse répartie dans le volume B d'un corps (la Terre dans notre cas) un potentiel newtonien. Ce potentiel joue un rôle tellement important en géodésie physique qu'il semble nécessaire d'en établir en détail les propriétés. A cette fin nous supposons que la densité ρ du corps attirant B est en général une fonction continue, mais qu'il peut exister un nombre fini de surfaces dans B sur lesquelles la densité est discontinue. Une telle fonction est appelée continue par morceaux. Nous ne ferons pas de distinction ici entre l'espace ponctuel et l'espace vectoriel associé, et nous écrirons pour les points quelconques P(x1,x2,x3) et Q(y1,y2,y3) aussi x et y, respectivement. Nous désignerons en général les éléments de volume par dτ et les éléments de masse par dM. Nous avons donc la relation :
dM = ρdτ.
Par conséquent, en portant notre attention sur le point Q en particulier, nous utiliserons indistinctement dτ(Q), dy3 ou dy1dy2dy3 pour l'élément de volume en Q, et dM(Q) ou dM(y) pour l'élément de masse en Q. En notation vectorielle nous écrirons donc
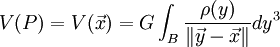
pour le potentiel de gravitation et
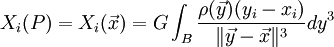
Soit
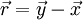
ri = yi–xi pour i=1,2,3.
La distance d(P,Q) entre P et Q peut s'écrire de l'une quelconque des façons suivantes
,
en sous-entendant implicitement que dans le dernier terme la sommation s'effectue pour toutes les valeurs de l'indice muet k qui se répète (convention de sommation d'Einstein).
Il est souvent avantageux d'écrire les intégrales plus haut sous la forme d'intégrale de Stieltjes, à savoir :
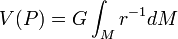
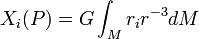
où M est la masse totale du corps B.
Bibliographie
- C. Denis (1985). The Hydrostatic Figure of the Earth, Geophysical Report 85/02, Institut d'Astrophysique, Université de Liège.
- C. Denis, E. Majewski, R. Teisseyre & J.B. Zieliński (1989). The Earth's Gravity Field, Chapitre 1, pages 1–77 de l'ouvrage collectif Physics and Evolution of the Earth's Interior, volume 4 : Gravity and Low-Frequency Geodynamics, édité par R. Teisseyre. Elsevier Publications, Amsterdam & PWN-Polish Scientific Publishers, Warszawa.
- N.M. Günter (1957). Die Potentialtheorie, und ihre Anwendung auf Grundaufgaben der mathematischen Physik, B.G. Teubner, Leipzig.
- O. Hölder (1882). Beiträge zur Potentialtheorie, Dissertation, Tübingen.
- O.D. Kellogg (1929). Foundations of Potential Theory, Springer-Verlag, Berlin (Dover reprint, 1953).
- W.D. MacMillan (1930). The theory of the potential, University of Chicago, Chicago (Dover reprint, 1958).
Existence et continuité du potentiel newtonien et de ses dérivées dans l'espace
Nous allons montrer maintenant que le potentiel V(P) et ses dérivées premières existent et sont continus dans tout l'espace pour des distributions de densité continues par morceaux. Comme le nombre de surfaces de discontinuité est fini, le corps B peut être subdivisé en un nombre fini N de corps plus petits Bk de masses Mk telles que
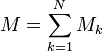
dans chacun desquels la densité est continue. On peut donc écrire
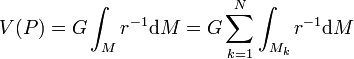
dans chacun desquels la densité est continue.
Existence et continuité du potentiel newtonien et de la gravité à l'extérieur de la matière
Si le point potentié P se trouve à l'extérieur de B, chacune des intégrales ∫Bk ρ(y) |y–x|-1 d³ dy existe, car la fonction ρ(y) |y–x|-1 est continue dans la region d'intégration. Puisque chaque intégrale existe séparément, leur somme existe aussi, et par conséquent V existe aux points extérieurs. En outre, puisque l'intégrand dans l'expression de V(P) est partout positif de même G, on a GM/rmin ≤ V(P) ≤ GM/rmax. Ici, rmin et rmax désignent respectivement les distances minimum et maximum entre le corps attirant et le point attiré P extérieur au corps. Lorsque P s'éloigne de B, à la fois rmin et rmax grandissent indéfiniment. On voit donc que V possède la limite zéro à l'infini, quelle que soit la direction envisagée. En termes plus précis, on dit que |V| se comporte régulièrement à l'infini et décroît comme d–1(O,P). En effet, soit Q un point intérieur quelconque. Alors la distance d(O,Q) est bornée et |d(O,P)–d(P,Q)| ≤ d(O,Q), de sorte que
d(O,P) V(P) = G ∫B ρ(Q) {1 - [d(O,P)–d(P,Q)]/d(O,P)}–1 dτ(Q) = G ∫B ρ(Q) dτ(Q) + termes d'ordre 1/d(O,P).
Par des arguments tout à fait similaires il est possible de prouver que Xi existe dans l'espace extérieur au corps B et que l'intensité du champ de gravité
X = (X1²+X2²+X3²)1/2
varie à grande distance comme d–2(O,P). De plus, il est évident que le potentiel et l'intensité de la gravité sont continus en des points extérieurs. Par la définition-même d'une dérivée, qui dans la théorie du potentiel est le plus souvent envisagée comme une dérivée directionnelle, la dérivation sous le signe intégrale est entièrement justifiée à l'extérieur du corps matériel. Soient h la longueur d'un petit segment de droite et xio un vecteur unitaire porté par l'axe Oxi. Alors, par définition :
∂iV = G limh=0 h–1 [∫M dM/r(x+ϑhxio,y) – ∫M dM/r(x,y)],
donc
∂iV = G limh=0 ∫M {∂i[ 1/r(x,y) + ½ h ∂i²[ 1/r(x+ϑhxio,y)]} dM(y),
où ϑ est un certain nombre compris entre 0 et 1. Comme
∂ir–1 = (yi–xi) r–3,
∂i²r–1 = 3 (yi–xi)² r–5 – r–3,
on a
|∂i²r–1(x+ϑhxio,y)| < 4 L–3
si L est la distance entre l'élément de masse dM(y) et le point P' positionné en x+ϑhxio. Supposons que Q' soit le point le plus proche de P' tel que Q' fasse encore partie de B. Alors d(P',Q') est la plus petite valeur possible de L, et
| ½ h ∫M ∂ir–1(x+ϑhxio,y) dM(y) | < ∫M 2 |h| dM(y) d–3(P',Q') = 2 M |h| d–3(P',Q').
Lorsque h tend vers zéro, le point P' se meut vers P. Pour cette raison, la distance minimum d(P',Q') de P' au corps peut changer. Toutefois, comme P se trouve à l'extérieur de la région B, il existe une valeur minimum de d(P',Q') non nulle lorsque |h| est suffisamment petit. Soit dmin
limh=0 | ½ h ∫M ∂ir–1(x+ϑhxio,y) dM(y) | < 2 M |h| dmin–3
s'annule avec h. Nous pouvons ainsi conclure qu'en tout point extérieur le gradient du potentiel de gravité existe et, à cause des expressions ci-avant fournissant Xi et ∂ir–1, représente bien la gravité :
∂iV = G ∫M ∂ir–1 dM = Xi.
Equation de Laplace

En fait, on peut étendre cette démonstration successivement à des dérivées d'ordres supérieurs et ainsi prouver que dans une région dépourvue de matière (c'est-à-dire dans l'espace vide), le potentiel gravitationnel possède des dérivées partielles continues de tous les ordres et est analytique.
En particulier, si nous considérons les dérivées partielles d'ordre 2, nous trouvons grâce à la relation ci-avant fournissant ∂i²r–1 que
(∂1² + ∂2² + ∂3²) r–1 = 3 [(y1–x1)² + (y2–x2)² + (y3–x3)²] r–5 – 3 r–3 = 0.
Nous aboutissons ainsi à la célèbre équation de Laplace
- (∂1² + ∂2² + ∂3²) V = G ∫M (∂1² + ∂2² + ∂3²) r–1 dM = 0.
Celle-ci est une équation aux dérivées partielles du second ordre qui doit être satisfaite par le potentiel gravifique dans les régions de l'espace dépourvues de matière. Elle joue un rôle fondamental, non seulement en géodésie, mais dans pratiquement toutes les sciences qui admettent une description mathématique des phénomènes. Nous rappelant la signification physique de l'opérateur laplacien (∂1² + ∂2² + ∂3²), nous savons que les fonctions qui obéissent à l'équation de Laplace, tel que le potentiel gravifique dans le vide, possèdent la propriété d'être des fonctions moyennes dans le sens que la valeur d'une telle fonction en un point est la moyenne des valeurs de cette fonction dans un voisinage suffisamment restreint de ce point. Une telle fonction est encore appelée fonction harmonique.
Existence du potentiel newtonien et de la gravité à l'intérieur de la matière
Pour établir les propriétés du potentiel gravifique à l'intérieur d'un corps matériel, en particulier à l'intérieur de la Terre, les démonstrations deviennent plus compliquées. Cela est dû au fait que pour des points intérieurs, l'intégrale V(x) = G ∫B ρ(y) |y–x|–1 d³y est impropre suite à la singularité qui se produit lorsque |y–x| = 0. Dès lors, la dérivation sous le signe d'intégration n'est plus permise sans justification aux points intérieurs. C'est la nécessité d'une telle justification qui complique les démonstrations. En effet, même l'existence et la continuité du potentiel en des points où il existe de la matière ne sont plus des propriétés évidentes, mais demandent une preuve. Supposons donc que P est un point intérieur. Afin de simplifier les démonstrations nous allons passer, sans perte de généralité, du système de coordonnées cartésiennes envisagé jusqu'à présent à un système de coordonnées sphériques (r,θ,λ) admettant P comme origine. On obtient ainsi :
r1 = y1–x1 = r sin θ cos λ, r2 = y2–x2 = r sin θ sin λ, r3 = y3–x3 = r cos θ.
Le vecteur x étant fixé, l'élément de volume en Q en termes des variables r,θ,λ est d³y = d³r = r² sin θ dr dθ dλ. Ayant défini la densité comme étant nulle en dehors de B, nous pouvons écrire
V(x) = G ∫D ρ(x+r) r–1d³r,
où le domaine d'intégration D possède une frontière sphérique de rayon L, centrée sur le point P. Nous prenons pour L la plus grande distance entre deux points arbitraires appartenant au corps matériel de dimensions finies B. Soit ρmax la valeur maximum de |ρ| dans D. Alors
V(P) ≤ 2πG ρmax L².
Ainsi, l'intégrale impropre V(x) ci-dessus converge uniformément par rapport aux paramètres x1,x2,x3, ce qui implique que le potentiel V existe en chaque point. D'une manière tout à fait similaire, nous pouvons prouver que les intégrales impropres définissant les composantes Xi(P) (i=1,2,3) de la gravité existent. En effet, en considérant encore des coordonnées sphériques et en gardant les mêmes notations comme ci-dessus, nous trouvons
|Xi(P)| = G | ∫D ri ρ(x+r) r–3d³r | ≤ 4πG ρmax L.
Ceci prouve la convergence uniforme, et donc l'existence, des intégrales impropres Xi.
Continuité du potentiel newtonien et de la gravité à l'intérieur de la matière
Nous montrons ensuite que le potentiel V est continu en un point Po de B. Ce n'est pas une restriction essentielle que de supposer que Po est à l'intérieur de B. En effet, nous avons vu que nous pouvons agrandir B en posant ρ(Q) = 0 dans la région qu'on ajoute. Le raisonnement classique consiste alors à décomposer le domaine B en deux sous-domaines, à savoir B–b et b. La sous-région b est une petite boule centrée sur Po. Nous écrivons
V(P) = V1(P) + V2(P)
moyennant
V1(P) = G ∫b ρ(Q) d–1(P,Q) dτ,
V2(P) = G ∫B–b ρ(Q) d–1(P,Q) dτ.
Or, pour ε > 0 donné arbirairement petit, nous pouvons prendre b suffisamment petit pour que
|V1(P)| < ⅓ ε,
indépendamment de la position de P. Pour ce faire, il suffit de prendre le rayon rb de b plus petit que [ε/(6πGρmax)]1/2, puisque dans ce cas il vient
|V1(P)| < 2πG ρmax rb².
Il s'ensuit que pour une telle sphère b on a
| V1(P) – V2(Po) | < ⅔ ε.
Alors, avec b fixé, il existe un voisinage de Po tel que, si P appartient à ce voisinage et Q appartient au sous-volume B–b, nous avons
| d–1(P,Q) – d–1(Po,Q) | < ε [3G (B–b) ρmax ]–1.
Ainsi, lorsque P est dans ce voisinage, nous trouvons
| V2(P) – V2(Po) ≤ G ∫B–b |ρ(Q)| | d–1(P,Q) – d–1(Po,Q) | dτ(Q) < ⅓ ε.
En combinant les inégalités pour V1 et V2, nous avons
| V(P) – V(Po) | < ε.
Ainsi V est continu en Po, et dès lors dans tout l'espace.
Comme précédemment, on établira la continuité de la gravité par une partition similaire de B en deux sous-régions. En effet, soit
Xi(P) = Xi(1)(P) + Xi(2)(P),
avec
Xik(P) = G ∫bk ρ(Q) ei d–2(P,Q) dτ(Q), k = 1, 2.
Ici nous utilisons les notations suivantes : b1 = b, b2 = B–b, e est le vecteur unitaire PQ0 :
|ei| ≤ (e1²+e2²+e3²)1/2 = 1.
Pour tout ε > 0 fixé arbitrairement petit, nous pouvons prendre le rayon de b plus petit que ε [12πG ρmax ]–1. Alors
| Xi(1)(P) | < ⅓ ε
indépendamment de la position de P, et
| Xi(1)(P) – Xi(1)(Po) | < ⅔ ε.
En outre, avec b fixé mais suffisamment petit et contenant les points P et Po, et avec Q appartenant au volume B–b, nous avons
| d–2(P,Q) – d–2(Po,Q) | < ε'/[3G {B–b) ρmax]
et
| Xi(2)(P) – Xi(2)(Po) | ≤ G ∫B–b |ρ(Q)| | d–2(P,Q) – d–2(Po,Q) | dτ(Q) < ⅓ ε'.
En combinant les inégalités pour Xi(1) et Xi(2), nous établissons la continuité du champ de force gravifique en tout point intérieur Po et, par conséquent, la continuité de la gravité dans tout l'espace rempli ou non de matière.
Existence et continuité des dérivées partielles du potentiel à l'intérieur de la matière
Toutefois, il n'est pas évident sans investigations complémentaires que les composantes de force Xi sont égales aux dérivées partielles ∂iV (i = 1,2,3) aux points où il y a de la matière. En effet, les conditions usuelles permettant de dériver sous le signe ∫ ne sont pas remplies par les intégrales impropres. Néanmoins, la relation Xi = ∂iV subsiste dans le cas présent. Pour le prouver, considérons deux points P et Po intérieurs à B, occupant par rapport à l'origine O les positions x et x + h xio, respectivement. Soit Q un point attirant occupant la position y. Par rapport à P, Q est situé en r = y–x. Considérons maintenant l'expression
I(h) = Xi(P) – h–1 [V(P) – V(Po)] = G ∫B [r–3 ri – h–1 (r–1 – ro–1)] ρ(r) d³r,
où
ri = yi – xi ,
r = d(P,Q) = |y – x| = (r1²+r2²+r3²)1/2,
ro = d(Po,Q) = |y – x – h xºi = (r²+h²–2hri)1/2.
Si nous arrivons à démontrer que la limite pour h tendant vers zéro de |I(h)| est plus petite qu'un nombre positif ε arbitrairement petit fixé à l'avance, alors nous pouvons conclure que la dérivée partielle ∂iV de V existe et est continue aux points intérieurs, tout comme pour les points extérieurs, et que sa valeur est Xi. Ainsi, prenons |h| assez petit pour que Po se trouve à l'intérieur du domaine sphérique b de rayon rb, centré sur P. La valeur rb elle-même est choisie assez petite de manière à ce que la boule b soit contenue entièrement dans le volume B. Ainsi, comme P et Po sont extérieurs au volume B–b, il résulte des propriétés du potentiel en des points extérieurs que, quelle que soit la valeur du rayon rb, la distance d(P,Po) = |h| < rb peut être prise suffisamment petite de manière à ce que
I2(h) = | G ∫B–b [r–3 ri – h–1 (r–1 – ro–1)] ρ(y) d³y < ½ ε.
En ce qui concerne la contribution I1(h) de l'intégrale prise sur le volume sphérique b, il convient de remarquer tout d'abord que
|ri| ≤ r
et que
r–1 – ro–1 = (ro – r)(r ro)–1.
Des relations exprimant les inégalités triangulaires appliquées au triangle PPoQ on déduit que
|ro – r| ≤ |h|.
D'autre part, comme
(r–1 – ro–1)² = r–2 + ro–2 – 2 r–1 ro–1 > 0,
il vient
(r ro)–1 < ½ (r–2 + ro–2) < r–2 + ro–2.
Ainsi, on aboutit à la majoration
| I1(h) | < G ∫b (2 r–2 + ro–2) ρ(y) d³y.
En posant comme de coutume ρ(Q) = 0 pour tout point Q se trouvant en dehors du volume B, nous pouvons écrire
| I1(h) | < 2G ∫b ρ r–2 dτ + G ∫bo ρ ro–2 dτ,
où
bo est un domaine sphérique de rayon 2rb centré sur Po. Ainsi, nous avons
| I1(h) | ≤ 16πGρmaxrb
Pour des valeurs de rb suffisamment petites, c'est-à-dire pour
rb < ε/[32πGρmax]
cette expression est numériquement inférieure à ½ε, et donc
| I(h) | ≤ | I1(h) | + | I2(h) | < ε.
De cette façon, nous avons prouvé que les dérivées partielles du premier ordre du potentiel existent et représentent les composantes de la gravité. Cette proposition est tout à fait générale. Elle est valable lorsque le point attiré se trouve à l'extérieur du corps qui attire, mais elle est aussi valable lorsque le point attiré se trouve à l'intérieur de ce corps. Une autre manière de s'exprimer consiste à dire que les dérivées de V du premier ordre s'obtiennent par dérivation sous le signe d'intégration.
Existence des dérivées partielles secondes du potentiel newtonien à l'intérieur de la matière
Il en va tout autrement des dérivées du second ordre à l'intérieur du corps. Le simple fait de supposer la densité continue et bornée ne suffit plus pour garantir l'existence de ces dérivées. Cela se voit clairement si nous dérivons formellement l'expression
∂iV(x) = –G ∫B r
par rapport à xj sous le signe d'intégration, et essayons de démontrer l'existence de ∂j∂iV comme auparavant pour V et ∂iV, en agrandissant le domaine B en un domaine sphérique D de rayon L centré sur P(x) et contenant B complètement. En effet, nous trouvons alors formellement
∂j∂iV(x) = –G ∫B ∂j(r
et
|∂j∂iV(x)| < ∫D 4G |ρ(r,θ,λ)| r–3 r² dr dθ dλ.
Condition de Hölder
Ici nous ne pouvons pas simplement remplacer |ρ| par sa borne supérieure ρmax pour pouvoir affirmer que l'intégrale du membre de droite existe, car l'intégrale impropre ∫0→L r–1 dr diverge. Nous imposons pour cette raison à la densité ρ(Q) une condition en P qui fut initialement introduite en 1882 par Otto Hölder, à savoir
- |ρ(Q) – ρ(P)| ≤ A rα
- pour tous les points Q tels que r = d(P,Q) ≤ c
- où A, α, c sont des constantes positives.
On peut montrer qu'une condition de Hölder est plus forte que la condition de continuité, mais plus faible que la condition de dérivabilité si α < 1. A fortiori elle est donc plus faible que la condition d'analyticité. S'il existe une région b dans laquelle ρ(Q) obéit à une condition de Hölder en chaque point, avec les mêmes valeurs de A, α et c, alors la fonction ρ(Q) est dite remplir une condition de Hölder uniformément dans b.
Un cas évident pour lequel une condition de Hölder uniforme s'applique est celui d'un domaine b\ dans lequel la densité est constante, soit ρ(Q) = ρo. Supposons que b est un volume sphérique de rayon rb et montrons que dans cet exemple les dérivées secondes de V existent en effet en un point intérieur P. Sans restreindre la généralité de la démonstration, nous pouvons supposer que le centre de b coïncide avec l'origine O des axes de coordonnées, et nous prenons le vecteur x = OP le long de l'axe Ox3. En termes des coordonnées sphériques (y,θ,λ), où y = (yk yk)1/2, θ = arcos(xk yk/xy), avec x = (xk xk)1/2, le potentiel en P engendré par toutes les masses dans b est fourni par
V(P) = 2πG ρo ( ⅓ x² – rb² ).
Etant une fonction scalaire, le potentiel gravifique est invariant par rapport aux changements du système de coordonnées. Par conséquent, cette formule est générale. Il s'ensuit qu'en chaque point à l'intérieur d'une masse sphérique homogène, nous avons
- V = 2πG ρo ( ⅓ xk xk – rb² ),
- ∂iV = 4πG ρo xi / 3,
- ∂j∂iV = 4πG ρo δji / 3.
Nous constatons, en particulier, que toutes les six dérivées partielles d'ordre 2 de V existent et sont continues. En outre, nous trouvons que
- ∂i∂iV = 4πG ρo.
Nous pouvons maintenant étudier les dérivées partielles du second ordre de V en un point intérieur quelconque P du domaine fini B, pour une distribution de densité générale satisfaisant une condition de Hölder du type ci-dessus. Comme précédemment, soit b un domaine sphérique de rayon rb centré sur P. Nous supposons que le volume b est entièrement contenu dans le volume B. Considérons alors séparément le potentiel V1(P) créé en P par toutes les masses dans b, et le potentiel V2(P) créé en P par toutes les masses restantes. Puisque P est un point extérieur pour l'évaluation de V2, ce potentiel possède des dérivées continues de tous ordres en P et y est harmonique, c'est-à-dire V2 est une solution de l'équation de Laplace en P. Ainsi, le problème est réduit à une étude de V1.
Si nous écrivons
ρ(Q) = ρ(P) + [ ρ(Q) – ρ(P) ],
nous voyons que le potentiel d'une sphère possédant une densité continue en P est la somme de deux potentiels : le potentiel créé par la sphère si elle était remplie de matière de densité constante égale à celle du point P, et le potentiel d'une sphère dont la densité s'annule en P. Comme nous venons juste de démontrer que le potentiel d'une sphère uniforme possède des dérivées continues du second ordre, il nous reste de discuter le cas dans lequel la densité s'annule en P et y remplit une condition de Hölder. En admettant que le rayon rb de la boule b est plus petit qu'une certaine constante positive c donnée, cela signifie que
|ρ1| ≤ A rα avec r = d(P,Q) ≤ rb ≤ c,
où ρ1 désigne la fonction ρ(Q)–ρ(P). Celle-ci engendre dans le volume b le potentiel V11 et le champ de force X1j(1), j = 1,2,3. Définissons la quantité
Jij(P) = – G ∫b ∂i ρ1 ∂j r–1 d³r,
qui devient successivement
Jij = – G ∫b ρ1 ∂i (r–3 rj) dτ = – G ∫b ρ1 (3 r–5 ri rj – r–3 δij) dτ.
Cette intégrale impropre, obtenue en dérivant formellement le potentiel gravifique V11 deux fois sous le signe intégrale, converge puisque
|Jij| ≤ 4 A G ∫b ρ1 rα–3 d³r ≤ 16 π G A α–3 ρ1 rbα
moyennant la condition de Hölder. Considérons maintenant au voisinage de P occupant la position x un point Po occupant la position x + h xio, de manière à ce d(P,Po) = |h| < rb. Formons l'expression
K(h) = h–1 [ X1j(1)(Po) – X1j(1)(P) ] + Jij
pour h ≠ 0. Cette intégrale est aussi convergente, comme on peut le constater en utilisant le même raisonnement que pour Jij, et parce que Xj existe aux points intérieurs. Nous avons
K(h) = G ∫b ρ1 { h–1 [ ( rj – h δij) ro–3 – rj–3 ] – ( 3 r–5 ri rj – r–3 δij )} d³r
avec ro² = r² + h² – 2 h ri. Nous voulons montrer que K(h) tend vers zéro avec h, indépendamment de la position de P. Mais pour arriver à cette fin, nous devons nous débarrasser de h dans le dénominateur du premier terme dans l'intégrale. En remarquant que
ro–3 – r–3 = [ r ro ( r + ro ) ]–1 ( r² – ro² ) ( ro–2 + r–2 + ro–1 r–1 ) = h ( 2 ri – h ) [ r ro ( r + ro ) ]–1 ( ro–2 + r–2 + ro–1 r–1 ),
nous trouvons
h–1 [ ( rj – h δij ) roK1(h)–3 – rj r–3 ] = – ro–3 δij + h–1 rj ( ro–3 – r–3 ) = – ro–3 δij + rj ( 2 ri – h ) [ r ro ( r + ro ) ]–1 ( ro–2 + r–2 + ro–1 r–1 ).
Pour h = 0, cette dernière expression se réduit à – r–3 δij + 3 r–5 ri rj, rendant ainsi l'intégrand de K(h) égal à zéro et, par conséquent, K(0) = 0. Si nous pouvons prouver que l'expression K(h) est continue par rapport à h en P, nous saurons qu'elle s'annule avec h, et il s'ensuivra que la dérivée de X1j(1) par rapport à xi existe en P et vaut Jij. Traçons donc une petite sphère de volume bε, de rayon rε < rb et de centre P, de sorte que |h| < rε. Comme P et Po sont tous les deux extérieurs au domaine b – bε, nous pouvons prendre |h| assez petit pour que la contribution K2(h) de l'intégration sur b – bε est plus petite en valeur absolue que ½ ε, où ε est un nombre positif fixé arbitrairement petit. Considérons maintenant la contribution K1(h) de l'intégration sur bε, à savoir
K1(h) = G ∫bε { – ro–3 δij + rj ( 2 ri – h ) [ r ro ( r + ro ( r + ro ) ]–1 ( ro–2 + r–2 + ro–1 r–1 ) – ( 3 r–5 ri rj – r–3 δij ) } ρ1 d³r.
En nous souvenant que rj et rj – h δij sont les j-ièmes composantes (pour i fixé) des vecteurs PQ et PoQ, respectivement, nous avons
|rj| ≤ r, |rj – h δij| ≤ ro, |2 ri – h| ≤ |ri| + |ri – h| ≤ r + ro.
Ainsi, l'expression entre crochets est bornée en valeur absolue par 4 r–3 + r–2 ro–1 + r–1 ro–2 + 2 ro–3. En utilisant alors la condition de Hölder, nous obtenons
K1(h) ≤ G A ∫bε [ 4 rα–3 + rα–2 ro–1 + rα–1 ro–2 + 2 rα ro–3 ] d³r ≤ 16πG A α–1 rεα + G A ∫bε [ rα–2 ro–1 + rα–1 ro–2 + 2 rα ro–3 ] d³r
Nous avons le droit de supposer α < 1, parce qu'une condition de Hölder avec un exposant donné implique toujours une condition avec un exposant positif plus petit. Cependant, dans ce cas, l'intégrand restant dans l'intégrale du membre de droite devient infini dans deux occasions, à savoir pour r = 0 et pour ro = 0. En considérant séparément les cas r < ro et ro < r, nous avons certainement
∫bε [ rα–2 ro–1 + rα–1 ro–2 + 2 rα ro–3 ] d³r < ∫bε 4 rα–3 d³r + ∫b'ε 4 roα–3 d³ro,
où b'ε est un domaine sphérique de rayon 2rε centré sur Po. Il s'ensuit que
|K1(h)| < 16πG (2+2α) A α–1 rεα.
En choisissant rε suffisamment petit pour que |K1(h)| < ½ ε, nous avons
|K(h)| < |K1(h)| + |K1(h)| < ε.
Ceci prouve que la fonction K(h) est continue par rapport à h en P, indépendamment de la position de P. Donc, l'existence des dérivées partielles du second ordre of V est établie et, en outre :
∂i ∂j V(P) = – ∂i Xj(P) = – ∂j Xi(P).
En particulier, le potentiel V11 pour lequel la densité vérifie une condition Hölder et qui s'annule en P est harmonique, puisque
∂i ∂i V11 = Jii = G ∫b ( 3 r–5 r² – 3 r–3 ) ρ1 d³r ≡ 0.
Équation de Poisson

Si nous superposons à la distribution de densité ρ1 s'annulant en P une autre distribution de densité ρ(P) constante partout dans le volume sphérique b, nous aboutissons au résultat suivant valable pour une distribution de densité continue dans un domaine sphérique satisfaisant à une condition de Hölder en P : les dérivées de la gravité existent, et
- ∇²V(P) = –4πG ρ(P),
où ∇² désigne l'opérateur laplacien (ou simplement le laplacien) ∂i ∂i. Finalement, si nous additionnons les potentiels des distributions extérieures à b, rien n'est contribué au laplacien et la même équation ci-dessus reste valable. Celle-ci est une équation aux dérivées partielles du second ordre, qui renferme l'équation de Laplace comme un cas spécial. Elle est connue comme équation de Poisson. Elle nous permet de trouver le potentiel si nous connaissons la densité et, réciproquement, trouver une distribution de densité si nous connaissons le potentiel. Elle est donc d'une importance capitale en géodésie physique et, plus précisément, pour le problème qui consiste à trouver la forme d'équilibre d'un corps en rotation. C'est pour cette raison que nous avons pris la peine dans cet article d'établir en détail l'équation de Poisson et d'autres propriétés importantes du potentiel newtonien.
Il convient de remarquer que nous avons pas discuté ici la situation prévalant en des points de la frontière du corps. En ces points-frontière, le potentiel d'une distribution de masse volumique, ainsi que ses dérivées premières, sont continues. Par contre, sur une frontière les dérivées secondes du potentiel n'existent pas en général. Il est clair qu'elles ne peuvent pas toutes être continues, car lorsque nous passons d'un point extérieur à un point intérieur au travers d'une frontière où la densité ne s'annule pas, ∇²V subit un saut de –4πGρ. Une situation semblable est réalisée sur des surfaces à l'intérieur d'un corps sur lesquelles la densité est discontinue. Alors, la valeur de ∇²V saute de –4πG Δρ lorsqu'on passe à travers la surface de discontinuité de densité, où Δρ désigne le saut de densité à travers cette surface.


















































