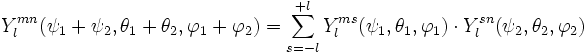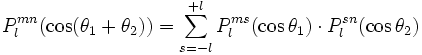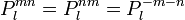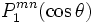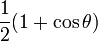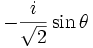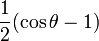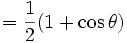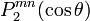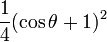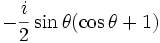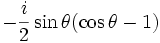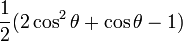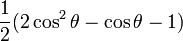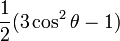Harmonique sphérique - Définition
On dit qu'une fonction est harmonique si son laplacien est nul.
Les polynômes harmoniques P(x,y,z), de degré l sont au nombre de 2l+1, et peuvent s'exprimer en coordonnées sphériques (
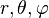
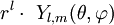
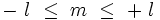
Tout polynôme homogène est entièrement déterminé par sa restriction à la sphère unité S² .
Définition : les fonctions sur la sphère obtenues par restriction de polynôme homogènes harmoniques sont des harmoniques sphériques.
Les harmoniques sphériques sont utilisées en physique mathématique, dès qu'intervient la notion d'orientation (anisotropie) et donc de rotation ( groupe de symétrie orthogonal SO3) et que le laplacien entre en jeu :
- en acoustique (reconstitution de l'effet d'espace par plusieurs haut-parleurs)
- en théorie du potentiel newtonien (électrostatique, mécanique),gravimétrie ...
- en géophysique (représentation du globe terrestre, en météorologie) et , en cristallographie pour la texture),
- en physique quantique (développement d'une fonction d'onde, densité du nuage électronique, description des orbitales atomiques de l'atome d'hydrogène)
- etc.
Base orthonormale des harmoniques sphériques
parmi les (2l+1) fonctions, l'habitude a été prise de sélectionner une base orthomormale sur la sphère S² munie de la mesure
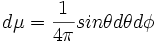
soit le produit scalaire ( hermitien en fait):
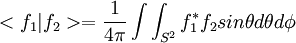
Les harmoniques sphériques sont les solutions de l'équation aux valeurs propres [1] :
|
|
où l'opérateur laplacien s'écrit en coordonnées sphériques sur la sphère de rayon unité, J² :
|
|
- elles sont fonctions propres de l'opérateur
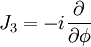
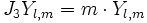
Celles-ci, une fois normées sur la sphère sont alors notées usuellement
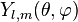
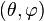
Expression des harmoniques sphériques
On obtient alors l expression inscrite plus bas. Une manière simple de retenir cette expression est la suivante :
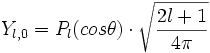
où Pl(x) est le polynôme de Legendre de degré l.
On obtient ensuite :
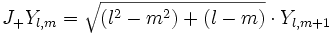
où
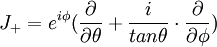
Pour m négatif ,
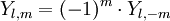
- Note : on pourra soi-même intuiter l'existence d'un opérateur d'échelle descendante, et vérifier la cohérence des résultats obtenus.
- Souvent cette base se note |lm> :
toute fonction sur la sphère S² pourra donc s'écrire :
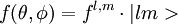
les coefficients complexes f(l,m) jouant le rôle de composantes de f dans la base des |lm> ( on dit parfois coefficients de fourier généralisés).
- en chimie ou en géophysique, il arrive qu on préfère utiliser les harmoniques sphériques "réelles" et des coefficients de fourier réels. Il n est pas difficile de s y adapter.
Recherche des harmoniques sphériques
On cherche les fonctions
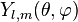
|
|
où k est une constante, qui sera fixée ultérieurement par la normalisation. L'équation aux valeurs propres devient une équation différentielle ordinaire du second ordre pour la fonction Pl,m(cosθ) :
|
|
On fait le changement de variable :
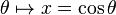
|
|
Les valeurs propres de cette équation sont indépendantes de m :
|
|
Les fonctions propres Pl,m(x) se construisent à partir des polynômes de Legendre Pl(x) qui sont les fonctions propres de l'équation différentielle ordinaire de Legendre, correspondant au cas m = 0 :
|
|
On a la formule génératrice d' Olinde Rodrigues :
|
|
On construit alors les fonctions propres Pl,m(x) par la formule :
|
|
soit explicitement :
|
|
Remarque : il suffit en pratique de calculer les fonctions Pl,m(x) pour
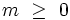
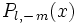
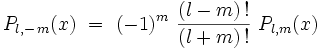
|
Normalisation
Les harmoniques sphériques constituent une base orthonormale de fonctions propres de l'opérateur laplacien sur la sphère de rayon unité S2 au sens où :
- elles sont orthogonales pour le produit scalaire suivant :
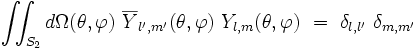
|
- Dans cette formule,
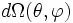
|
|
- toute fonction
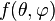
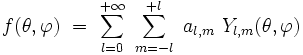
|
- où les coefficients complexes al,m se calculent par :
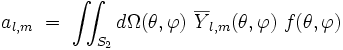
|
Expression des harmoniques sphériques normalisées
Les harmoniques sphériques généralisées sont définies sur la sphère S3. La normalisation des harmoniques sphériques conduit à l'expression finale :
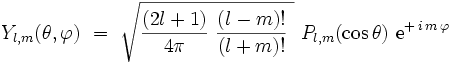
|
Propriétés
Les harmoniques sphériques formant une base orthogonale sur la sphère unité, toute fonction continue ƒ(θ,φ) se décompose en une série d'harmoniques sphériques :
où l' et m sont des indices entiers, Clm est un coefficient constant et souvent en mathématiques prend le nom de coefficient de Fourier généralisé relativement à cette base.
Le développement en harmoniques sphériques est l'équivalent, appliqué aux fonctions angulaires, du développement en séries de Fourier pour les fonctions périodiques.
Ylm est la partie réelle d'une fonction complexe Ylm
Ylm est appelée " fonction associée de Legendre " et est définie par
où i est l'imaginaire et Plm est le polynôme de Legendre :
On a donc
On a par exemple :
-
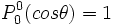
-
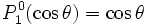
-
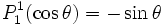
-
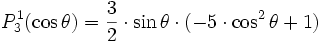
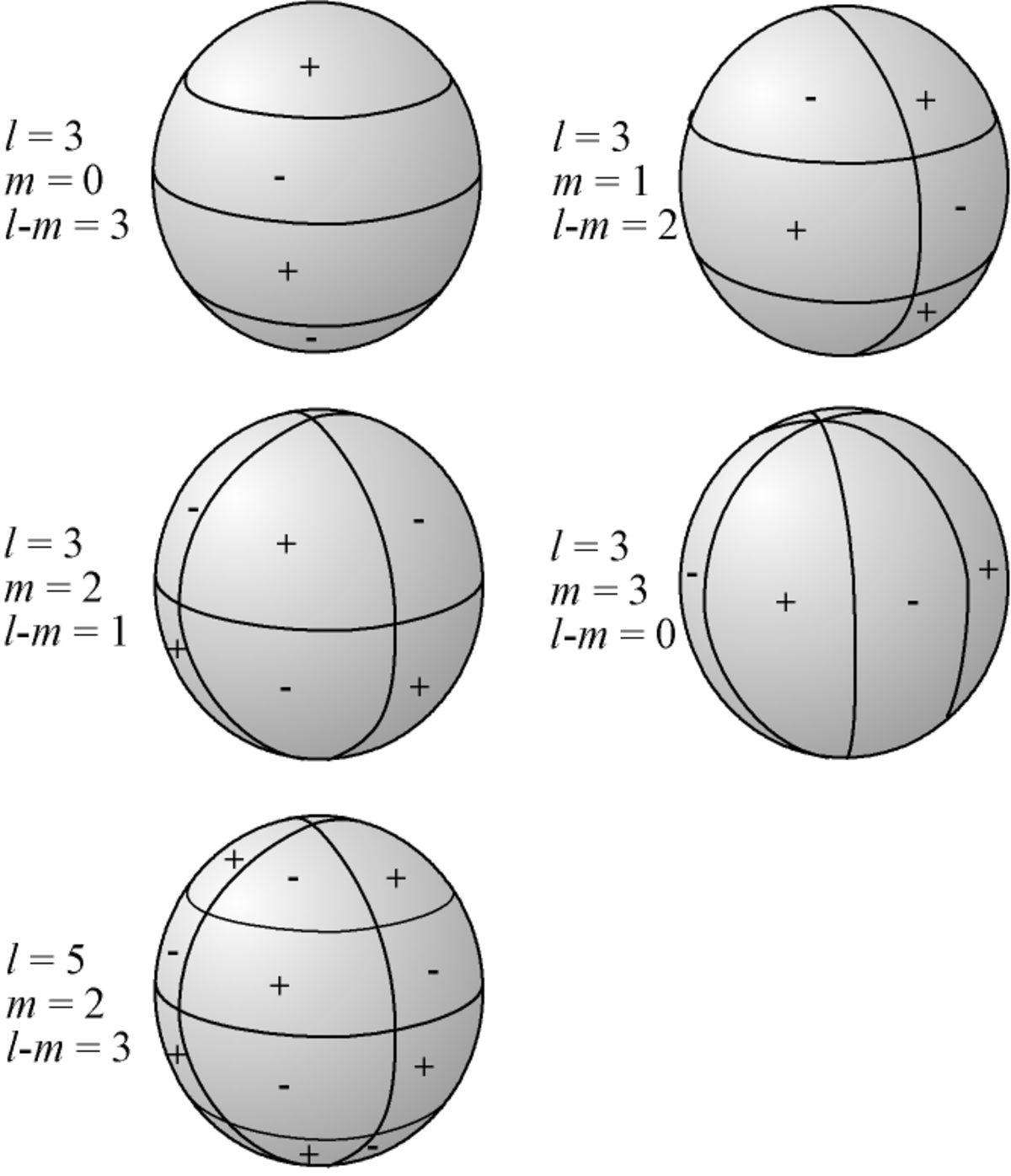
Les fonctions Ylm(θ,φ) présentent de plus en plus de symétries au fur et à mesure que l croît (sauf lorsque l = 0, puisque Y00 est une fonction constante et décrit donc une sphère).
Si l'on utilise la représentation sphérique
alors la surface représentatrice est une sphère bosselée ; les bosses correspondent aux parties où Ylm est positif, les creux aux parties où Ylm est négatif. Lorsque θ et φ décrivent l'intervalle [0;2π[, Ylm(θ,φ) s'annule selon l cercles :
- m cercles suivant un méridien, une iso-longitude (intersection entre un plan contenant Oz et la sphère) ;
- l-m cercles suivant un parallèle, une iso-latitude (intersection entre un plan parallèle à Oxy et la sphère).
Le paramètre l est appelé le " degré ", m est appelé l'" ordre azimutal ". Entre les cercles d'annulation, la fonction est alternativement positive ou négative.
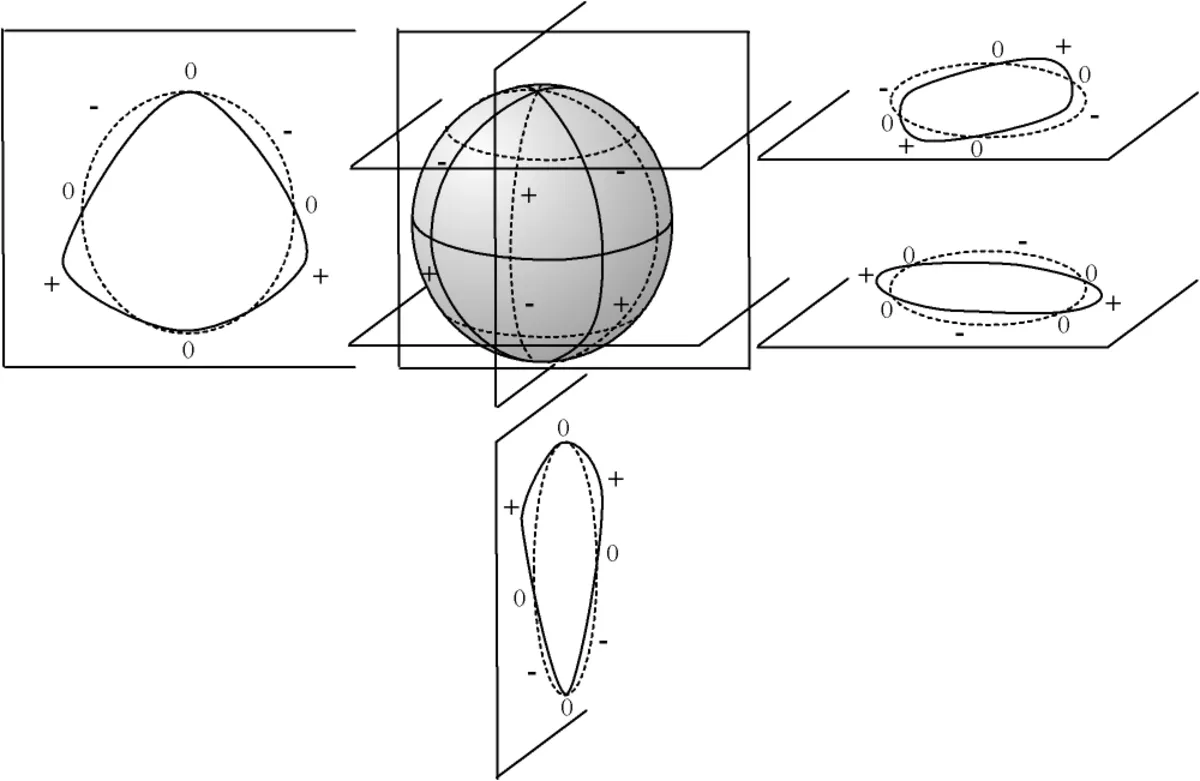
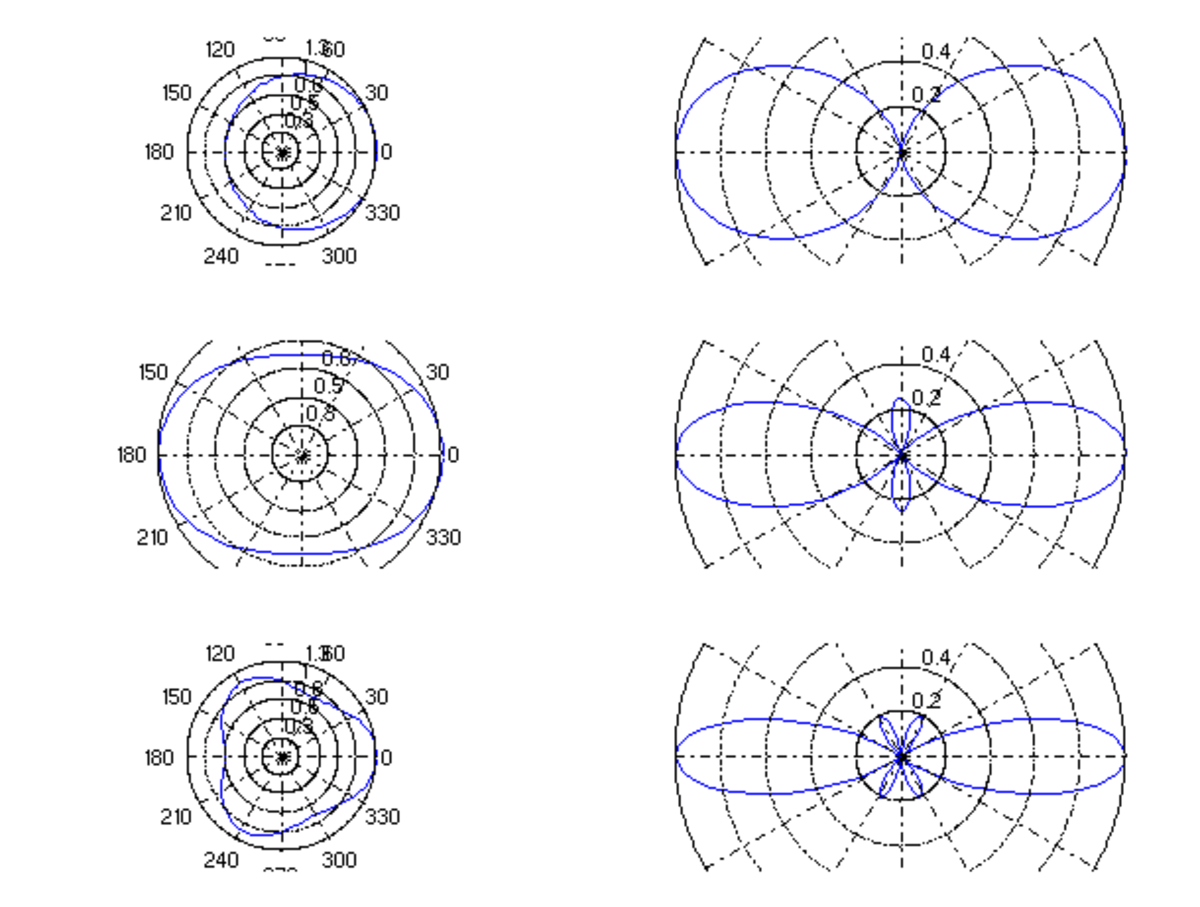
Nous représentons ci-dessous quatre coupes de l'harmonique sphérique Y32 :
Comme précédemment, on peut représenter la fonction par la courbe en coordonnées sphériques
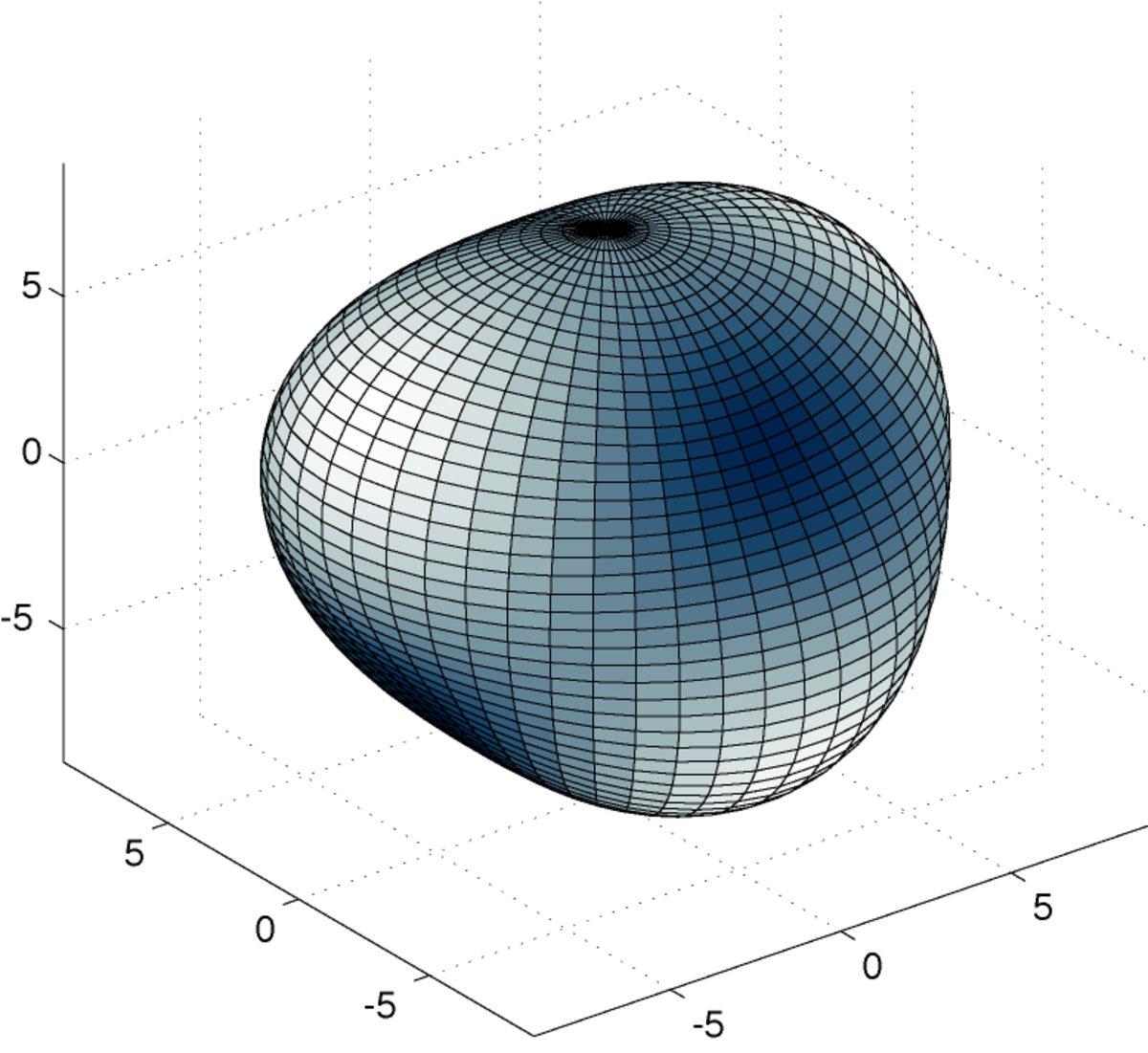
|
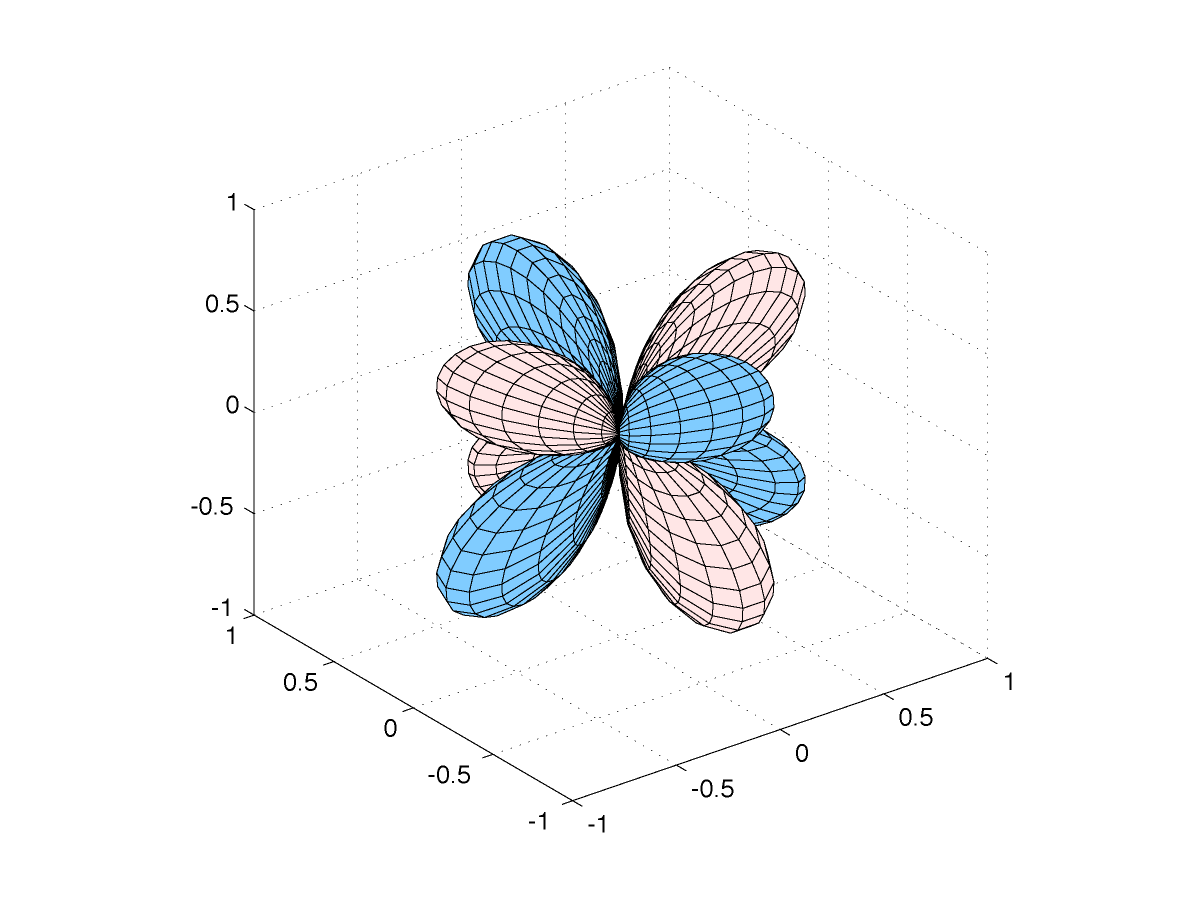
|
|
les parties en blanc sont positives, en bleu négatives |
|
Représentation graphique
On peut représenter les harmoniques circulaires de trois manières :
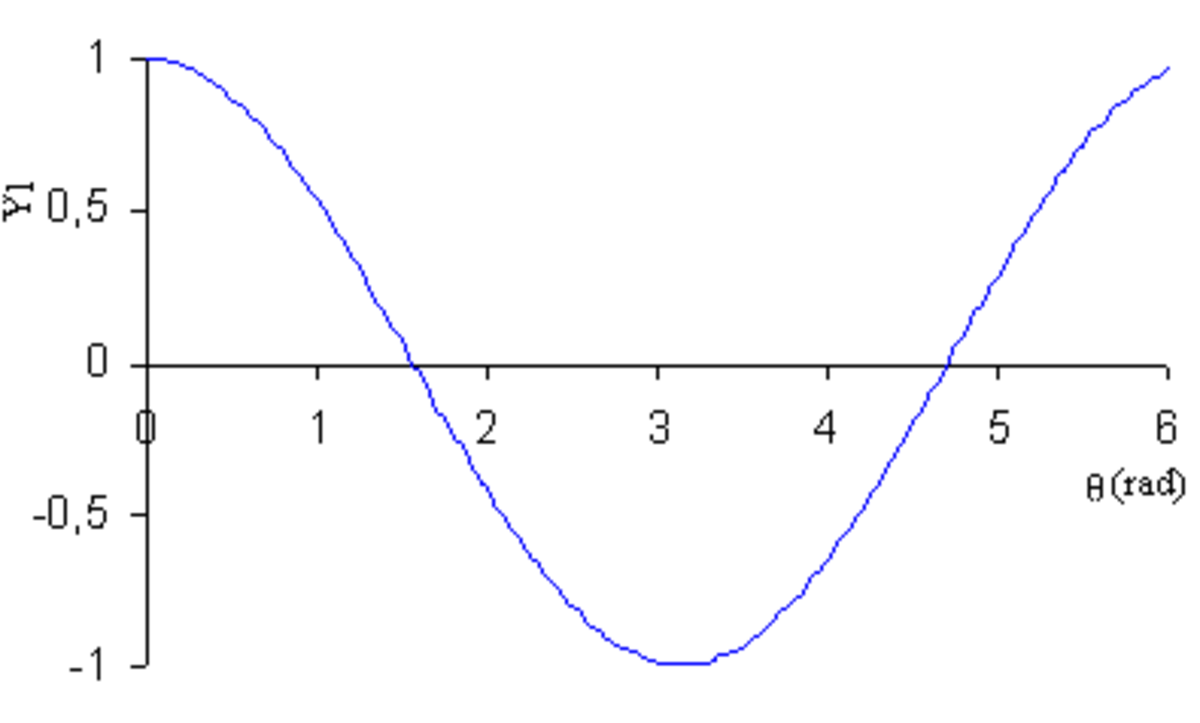
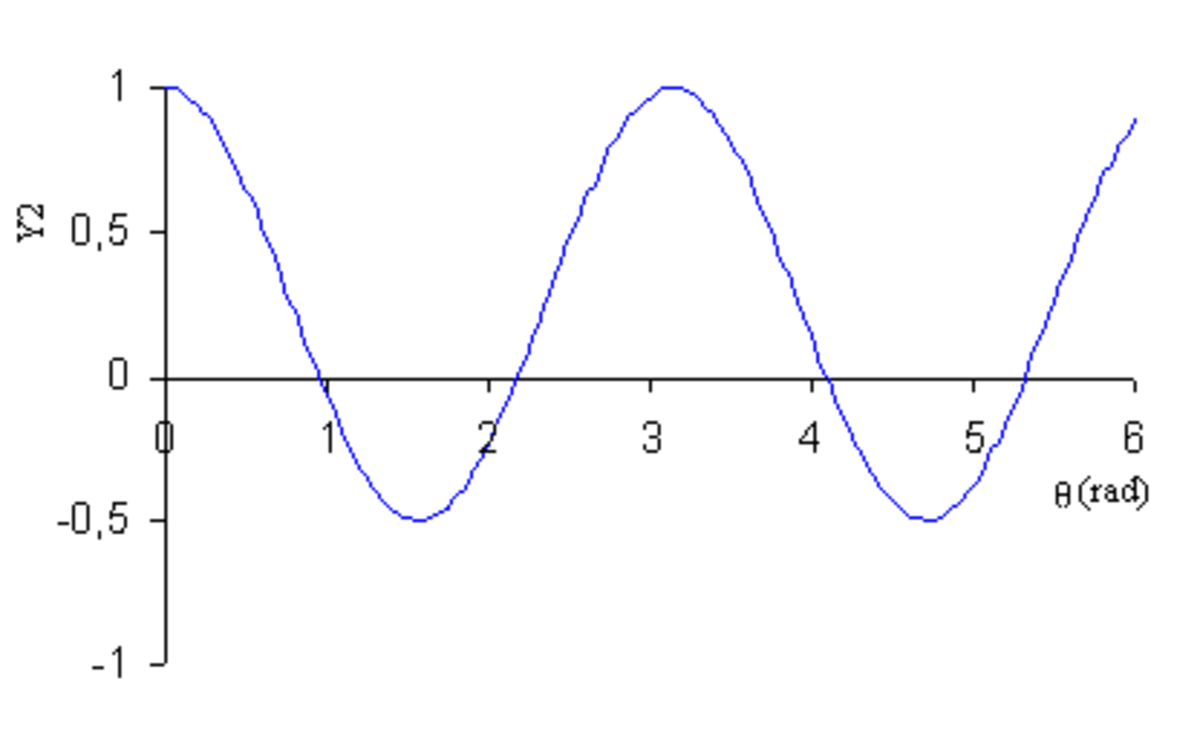
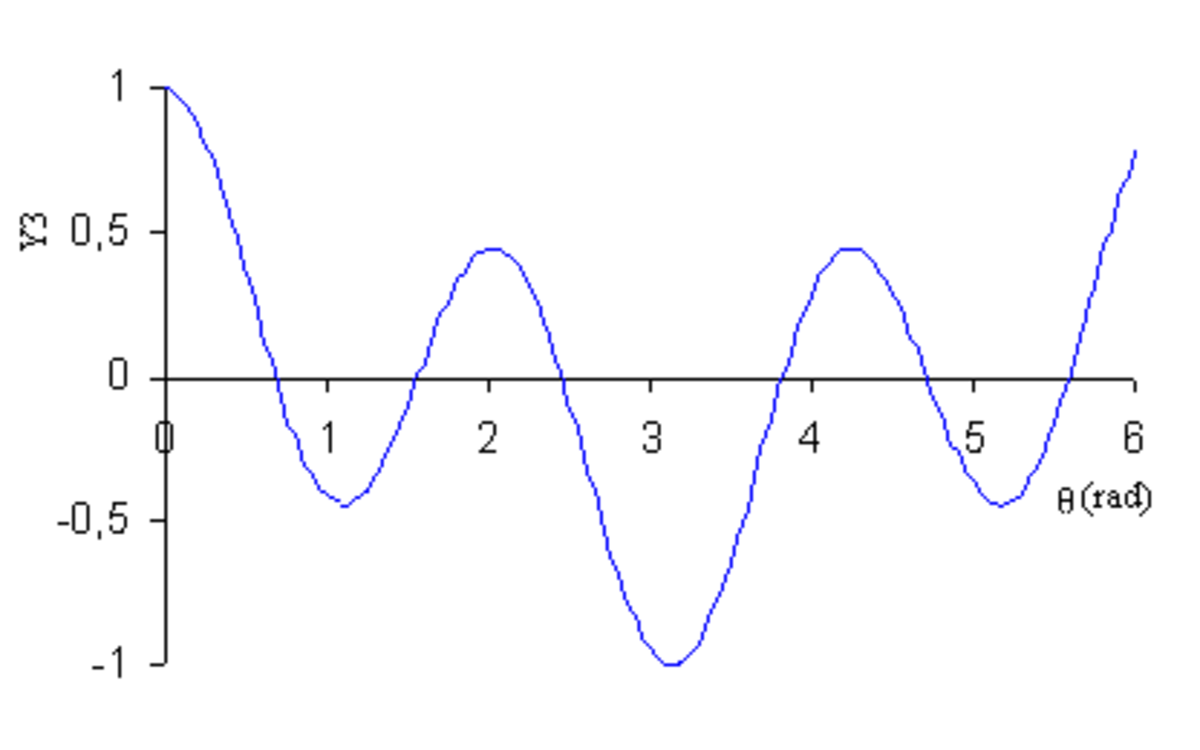
- en coordonnées cartésiennes : y = Yl(θ) ;
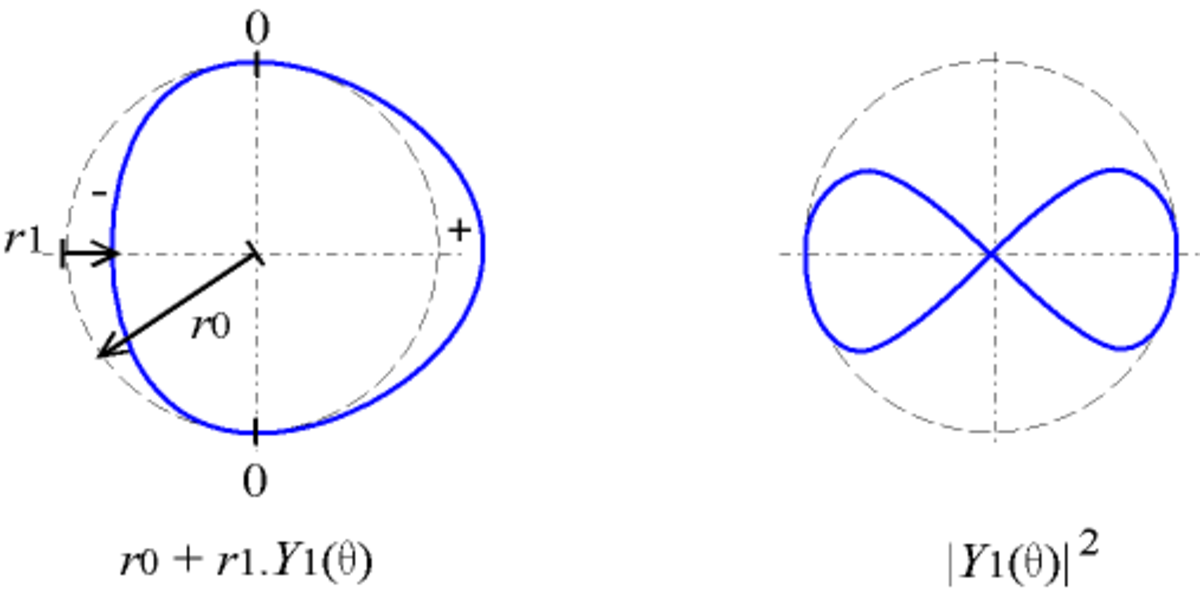
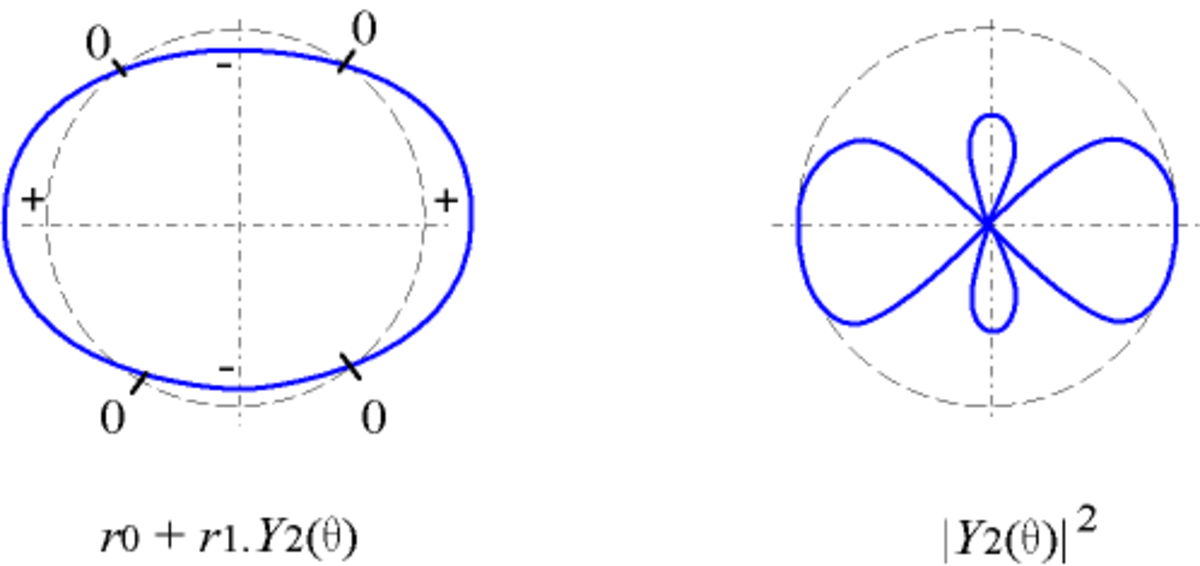
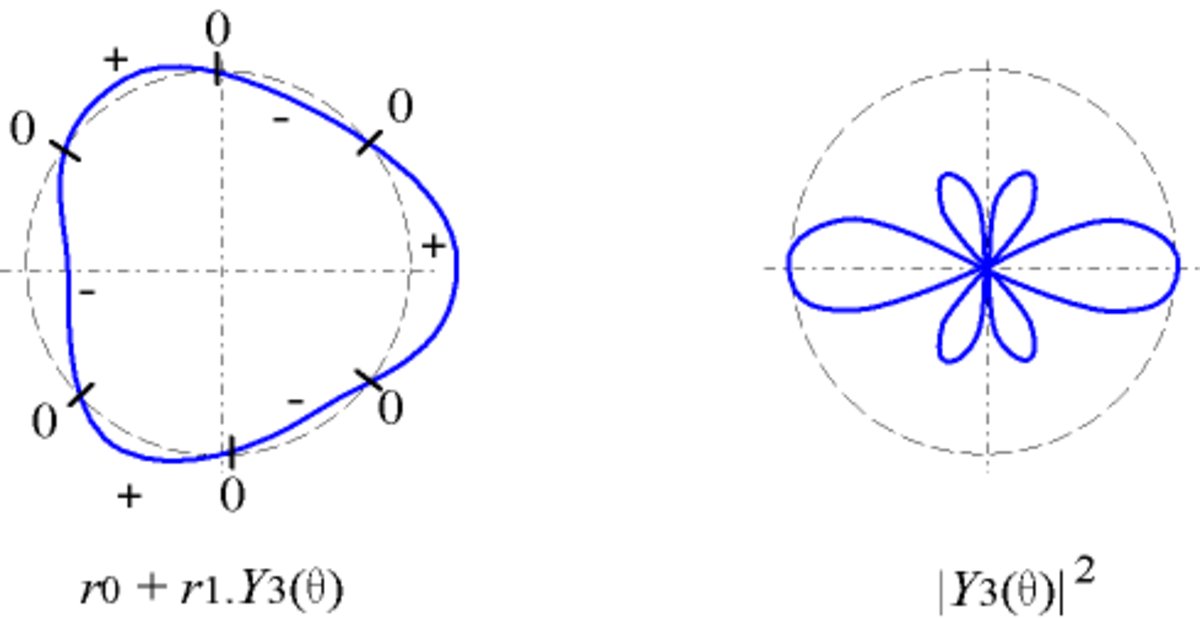
- en coordonnées polaires :
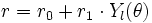
avec r1 < r0, utilisé par exemple pour un objet circulaire ; la courbe coupe le cercle de centre O et de rayon r0 lorsque la fonction s'annule ; - en coordonnées polaires : r = | Yl(θ) | 2
utilisé par exemple pour les fonctions d'onde en physique quantique.
| Représentation cartésienne | Représentations polaires (tracé manuel) | |
|---|---|---|
| Y1 |
|
|
| Y2 |
|
|
| Y3 |
|
|
Harmoniques circulaires
Définition
Dans le plan, la décomposition s'écrit :
Y0 est une fonction constante, la courbe représentatrice en coordonnées polaires r = Y0(θ) est donc un cercle de rayon r0.
Yl est une fonction invariante par une rotation d'un angle de 1/(l+1) tour, c'est-à-dire que
on dit que Yl admet une symétrie d'ordre l+1.
Polynômes de Legendre
Pour les harmoniques circulaires, on utilise des polynômes Pl de la fonction cosinus :
- Yl(θ) = Pl(cosθ)
Les polynômes Pl utilisés sont les polynômes de Legendre1 :
-
![P_l(X) = \frac{1}{2^l \cdot l!} \cdot \frac{\partial^l}{\partial X^l}\left [ (X^2 - 1)^l \right ]](https://static.techno-science.net/illustration/Definitions/autres/2/21ebce587abea5b6902162cb11cf3451_65e04405472ebe0e799bad2f363916f1.png)
- (formule de Rodrigues, mathématicien français)
On obtient :
- P0(cosθ) = 1 (fonction isotrope) ;
- P1(cosθ) = cosθ ;
-
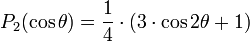
-
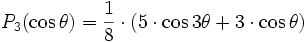
Harmoniques sphériques généralisées
Lorsque l'on considère l'orientation d'un objet dans l'espace, il faut faire appel à trois angles ; on utilise en général les angles d'Euler (ψ,θ,φ).
Considérons une fonction continue de l'orientation ƒ(ψ,θ,φ) ; comme précédemment, cette fonction peut être décomposée en harmoniques sphériques généralisées
où Clmn est une constante. La fonction Ylmn s'écrit :
Le polynôme Plmn est le polynôme de Legendre généralisé
Quand X décrit l'intervalle [-1;1], cette fonction Plmn est soit réelle, soit imaginaire pure. Y000(ψ,θ,φ) est la fonction isotrope (symétrie sphérique).
D'après la loi de composition des rotations, on a :
et en particulier
On a de manière générale :
Par exemple pour l = 1 :
| m | n | ||
|---|---|---|---|
| -1 | 0 | +1 | |
| -1 |
|
|
|
| 0 |
|
cosθ |
|
| 1 |
|
|
|
Pour l = 2 :
| m | n | ||||
|---|---|---|---|---|---|
| -2 | -1 | 0 | +1 | +2 | |
| -2 |
|
|
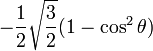
|
|
|
| -1 |
|
|
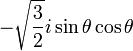
|
|
|
| 0 |
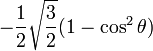
|
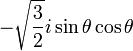
|
|
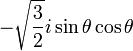
|
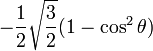
|
| 1 |
|
|
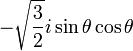
|
|
|
| 2 |
|
|
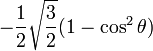
|
|
|
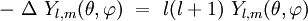
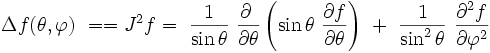
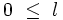
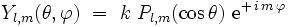
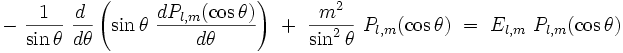
![- \ \ \frac{d ~}{dx} \left[ (1-x^2) \ \frac{d P_{l,m}(x)}{dx}\right] \ + \ \frac{m^2}{(1-x^2) } \ P_{l,m}(x) \ = \ E_{l,m} \ P_{l,m}(x)](https://static.techno-science.net/illustration/Definitions/autres/3/3496f4756365466deaf2b5bf987f1ee7_9b0c64958778f2cb6cfff777a6cc941b.png)
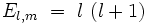
![- \ \ \frac{d ~}{dx} \left[ (1-x^2) \ \frac{d P_{l}(x)}{dx}\right] \ = \ l \ (l+1) \ P_{l}(x)](https://static.techno-science.net/illustration/Definitions/autres/0/0f40b6f108fa031f4268887ed724a77c_286051122177c996ecc13618922016ad.png)
![P_{l}(x) \ = \ \frac{1}{2^l \ l !} \ \frac{d^l ~}{dx^l} \left[ x^2 - 1 \right]^l](https://static.techno-science.net/illustration/Definitions/autres/2/2c560dc44a1b4147e0c5add6238d801c_f1792eb4d0d76d0691d2d190cf3db26c.png)
![P_{l,m}(x) \ = \ (-1)^m \ \left[ 1 - x^2 \right]^{m/2} \ \frac{d^m P_{l}(x)}{dx^m}](https://static.techno-science.net/illustration/Definitions/autres/f/f3e2e43ef8497a03ab7d9ca469b6fbe0_a281108a4ff4ed1322f058807204b4ad.png)
![P_{l,m}(x) \ = \ \frac{(-1)^m}{2^l \ l !} \ \left[ 1 - x^2 \right]^{m/2} \ \frac{d^{l+m} ~}{dx^{l+m}} \left[ x^2 - 1 \right]^l](https://static.techno-science.net/illustration/Definitions/autres/c/cdf7d1432fddacc6fd126031d1537b03_045888fb33fc3eafc62d6a500b04191b.png)
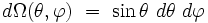
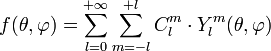
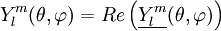
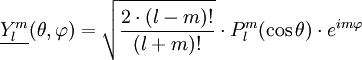
![P_l^m (X) = \frac{(-1)^m}{2^l \cdot l!} \cdot (1-X^2)^{m/2} \cdot \frac{\partial^{m+l}}{\partial X^{m+l}} \left [ (X^2 - 1)^l \right ]](https://static.techno-science.net/illustration/Definitions/autres/8/8c71ea661b31ce0fcdd649cedc1b64df_2a4e784d873b7e735fdcc7b005bfa4ed.png)
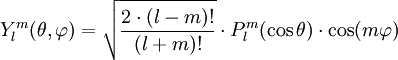
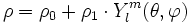
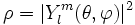
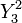
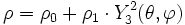
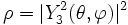
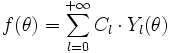
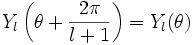
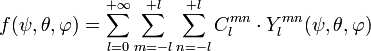
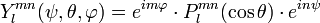
![P_l^{m n} (X) = \frac{(-1)^{l-m} \cdot i^{n-m}}{2^l \cdot (l-m)!} \cdot \left [ \frac{(l-m)! (l+n)!}{(l+m)! (l-n)!} \right ]^{1/2} \cdot (1-X)^{-\frac{n-m}{2}} \cdot (1+X)^{-\frac{n+m}{2}} \cdot \frac{\partial^{l-n}}{\partial X^{l-n}} \left [ (1-X)^{l-m} (1+X)^{l+m} \right ]](https://static.techno-science.net/illustration/Definitions/autres/8/8c6f4cd197a0bb0bcccad9547bf51582_f4fd9068795d8099e8c5eef699687241.png)