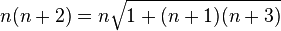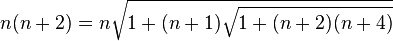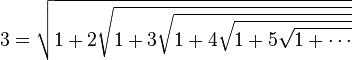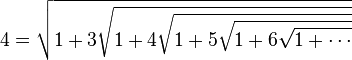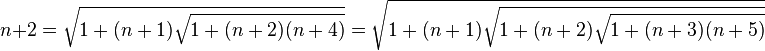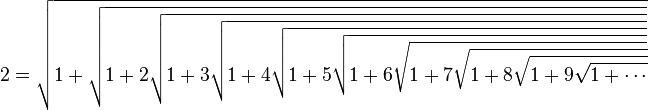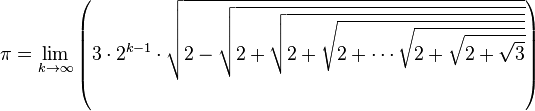Racine carrée - Définition
En mathématiques, la racine carrée d’un nombre x est un nombre dont le carré (la multiplication du nombre par lui-même) vaut x. Tout nombre réel positif possède une racine carré positive unique, appelée racine carrée principale et notée
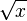
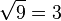
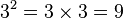
D'après le théorème fondamental de l'algèbre, l'équation définissant la racine carrée d'un nombre quelconque possède toujours deux solutions (qui peuvent être égales entre elles). Pour un nombre réel positif, ses deux racines carrées sont la racine carrée principale et la racine carrée négative (notée
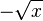
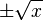
La racine carrée d'un nombre entier qui n'est pas un carré parfait est toujours un nombre irrationnel, c'est-à-dire qu'il ne peut être exprimé par une fraction. Par exemple,
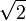
Le signe
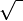
Définition
L’application
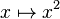
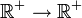
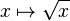
Mise en garde : l’aire s’exprime dans le système universel en mètre carré et les longueurs en mètre. En prenant la racine carrée d’une quantité exprimée en mètres carrés, on obtient une quantité exprimée en mètres. Les physiciens attachent une importance particulière à l’analyse des unités ; cet aspect est effacé en mathématiques. Les nombres réels sont des constantes sans unité, et la racine carrée d’un nombre réel positif est un nombre réel positif.
Analyse
La fonction racine carrée vérifie les propriétés élémentaires suivantes valables pour tous nombres réels positifs x et y :
-
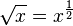
-
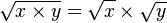
-
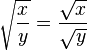
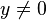
-
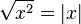
La fonction racine est continue en tout réel positif x (pour y proche de x,
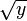
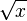
La fonction dérivée de
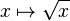
La fonction racine est en réalité de classe
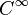
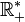
Mieux encore, la fonction racine est développable en séries entières. Le développement en série de Taylor de la fonction racine carrée au point 1 s’obtient immédiatement à partir de la formule du binôme généralisée :
pour tout réel |h| < 1.
Remarquons au passage que
et est donc un entier naturel[réf. nécessaire].
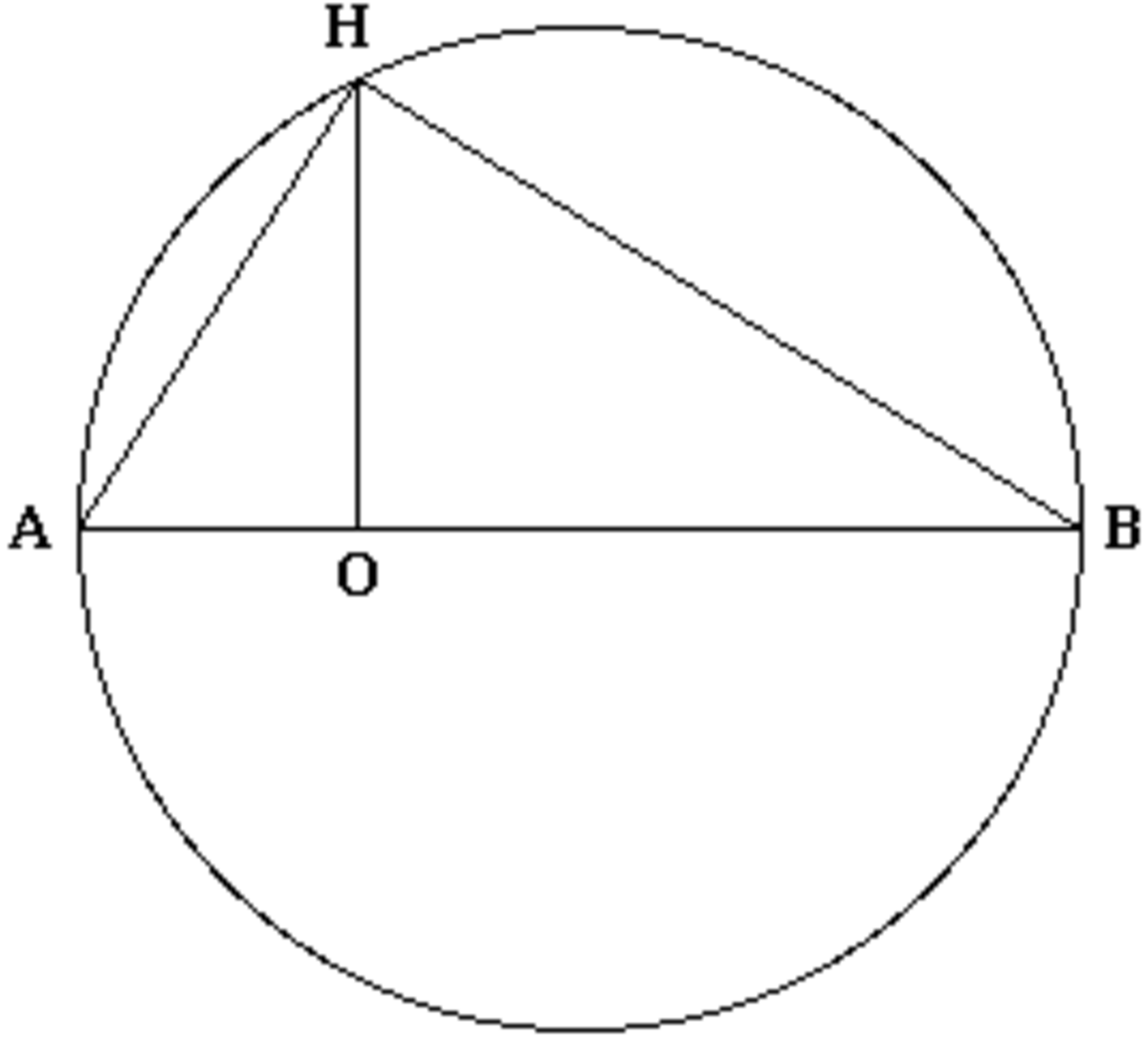
Construction géométrique de la racine carrée
La construction géométrique suivante se réalise à la règle et au compas et permet, étant donné un segment 0B de longueur a de construire un segment de longueur
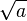
- Construire le segment AB de longueur 1+a et contenant le point O avec AO = 1
- Construire le cercle C de diamètre AB.
- Construire la droite D perpendiculaire à (OB) et passant par O.
- Nommer H le point d’intersection du cercle C et de la droite D.
Le segment OH est de longueur
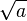
La preuve consiste à appliquer le théorème de Pythagore :
- Au triangle rectangle HOB : OH2 + a2 = HB2
- Au triangle rectangle ABH : HB2 = (a+1)2 - AH2
- Au triangle rectangle AOH : AH2 = 12 + OH2
D’où OH2 + a2 = (a+1)2 - (12 + OH2), soit, après simplification OH2 = a, et donc
Cette construction a son importance dans l’étude des nombres constructibles.
Les racines carrées de nombres complexes
La racine carrée sur

Pour tout nombre complexe non nul z, il existe exactement deux nombres complexes w tels que w2 = z. Pour des raisons de nature topologique, il est impossible de prolonger la fonction racine carrée
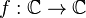
On appelle détermination de la racine carrée sur un ouvert U de

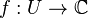
La détermination principale de la racine carrée est la fonction
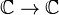
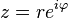
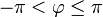
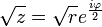
Quand le nombre est dans sa forme algébrique, on a :
où le signe de la partie imaginaire de la racine est le même que le signe de la partie imaginaire du nombre initial (si elle est nulle, on prend par convention le signe +).
Notons qu’à cause de la nature discontinue de la détermination principale de la racine carrée dans le plan complexe, la relation
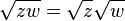
Extension des racines carrées en algèbre
Soient x et a deux éléments d’un anneau A, tels que x2=a. Un abus de langage est d’écrire
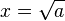
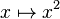
Les racines carrées de matrices et d’opérateurs
Si A est une matrice symétrique définie positive ou un opérateur autoadjoint défini positif en dimension finie, alors il existe exactement une matrice symétrique définie positive ou un opérateur autoadjoint défini positif B tel que B2 = A. On pose alors : √A = B.
Plus généralement, pour toute matrice normale ou tout opérateur normal en dimension finie A, il existe des opérateurs normaux B tels que B2 = A. Cette propriété se généralise à tout opérateur borné normal sur un espace de Hilbert.
En général, il y a plusieurs tels opérateurs B pour chaque A et la fonction racine carrée ne peut pas être définie pour les opérateurs normaux d’une façon satisfaisante (continue par exemple). Les opérateurs définis positifs sont apparentés à des nombres réels positifs, et les opérateurs normaux sont apparentés à des nombres complexes. Les articles sur la théorie des opérateurs développent d’avantage ces aspects.
Extraction de racines carrées
Un premier algorithme
Nous allons exposer un algorithme qui va nous permettre d’extraire la racine carrée d’un nombre. Évidemment, si la racine carrée n’est pas un nombre décimal, alors l’algorithme ne se termine jamais, mais on s'approche autant qu'on peut le souhaiter du résultat : la suite des chiffres est exacte.
Nous commençons par séparer les chiffres du nombre par paires en commençant à partir de la virgule. Nous plaçons le nombre dont on veut extraire la racine en haut, de la même façon que lorsque nous effectuons une division selon la méthode classique ; la racine carrée sera inscrite au-dessus de ce nombre.
À chaque étape :
- on abaisse la paire de chiffres la plus significative non encore utilisée et on la place au côté d’un reste éventuel de l'étape précédente ;
- soit r le résultat intermédiaire de la racine carrée obtenu précédemment (égal à zéro au début). On cherche le plus grand chiffre x tel que le nombre y=(20r + x)x ne dépasse pas la valeur courante. On place ce nouveau chiffre x sur la ligne supérieure au dessus de la paire abaissée ;
- on soustrait y de la valeur courante pour former un nouveau reste ;
- si le reste est nul et qu’il n’y a plus de chiffre à abaisser alors l’algorithme se termine sinon on recommence.
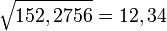
(nota : la suite des chiffres en gras s'inscrit au fur et à mesure au dessus du nombre initial, au dessus de la paire de chiffre traité selon l'algorithme, et donne le résultat : 12,34 . La place de la virgule est significative mais n'a pas besoin d'être prise en compte pendant les calculs, il suffit de la constater à la fin)
1 2 3 4 01 52,27 56 1 r=0 à cette étape x=1 01 1 y=(20*0+1)1 = 1 <= 01 alors que (20*0+2)* = 4 > 01 donc x = 1 ____ __ j'inscris le 1: r=1 pour l'étape suivante 00 52 2x je pose 01-01=00 et j'abaisse 52: apparait 52 x=2 00 44 12 y=(20*1+2)2 = 44 <= 52 alors que 20*1+3*3= 69 > 52 donc x = 2 _______ __ j'inscris le 2: r=12 pour l'étape suivante, 20*r = 240 08 27 24x 52-44 = 08, je pose 08 et j'abaisse 27: apparait 827 x=3 07 29 123 y=(20*12+3)*3 = 243*3 = 729 < 827 _______ __ j'inscris le 3: r=123 pour l'étape suivante, 20*r=2460 98 56 246x 827-729 = 98, je pose 98 et j'abaisse 56: apparait 9856 x=4 98 56 1234 y=(20*123+4)*4 = 9856 _______ j'inscris le 4: r=1234 00 -- 9856-9856 = 0 et il n'y a plus rien à abaisser: fin de l’algorithme
Vérification :
12,34 × 12,34 = 12×12 + 2×12×0,34 + 0,34×0,34. = 144 + 8,16 + (0,32×0,32 + 2×0,02×0,32 + 0,02×0,02) = 144 + 8,16 + 0,1024 + 0,0128 + 0,0004 = 152,2756
Jusqu’au XIXe siècle on utilisait couramment cet algorithme en accélérant les calculs à l’aide d’un abaque formée d’un jeu de réglettes: les bâtons de Napier.
Bien que décrite ici pour des nombres écrits en base 10, la procédure fonctionne dans n’importe quelle base, base 2 comprise. Dans ce qui précède, 20 représente le double de la base, et en binaire ce nombre serait remplacé par 100.
La méthode de Héron
La méthode de Héron est un algorithme permettant d’approcher les racines carrées. Son importance est avant tout historique, elle a été développée par les Babyloniens. Il fournit de bonnes approximations au prix de quelques divisions.
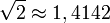
- Prenons la valeur rapprochée
-
- On a ainsi obtenu la racine carrée de 2 à la précision 10 − 4.
On peut avoir une approche plus algorithmique en simplifiant cette méthode par la formule de Newton
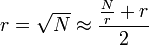
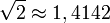
- Prenons de nouveau la valeur rapprochée
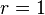
-
- On obtient la racine carrée de 2 à la précision 10 − 4.
- En appliquant cette formule on pourra écrire en langage basic:
- N = 2 /* Nombre dont on cherche la racine carrée
- r = 1 /* r = valeur rapprochée = 1
- DO /* Début de la boucle
- r = (r + (N / r)) / 2 /* Approximation
- PRINT "Racine de ";N;" ~= ";r /* Affichage du résultat
- LOOP /* Fin de la boucle
Calcul par la méthode du goutte à goutte
Les racines carrées, approximations entières
Les concepteurs de présentations de jeux vidéos ont parfois besoin de construire des tables des parties entières des racines carrées des entiers naturels. Les premières sont données par:
| CARRE | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | .. | 15 | 16 | 17 | .. | 24 | 25 | 26 | 27 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RACINE | 0 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | .. | 3 | 4 | 4 | .. | 4 | 5 | 5 | 5 |
Une observation des premiers termes montrent que la suite stationne d’entiers en entiers, et saute successivement d’un incrément de manière régulière. Plus précisément,
- le 0 est répété 1 fois,
- le 1, 3 fois
- le 2, 5 fois
- le 3, 7 fois
- le 4, 9 fois
Le nombre de fois que l’entier n est répété est le n-ième entier impair. La preuve repose sur l’identité suivante:
Formulaire
L’identité
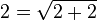
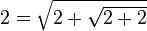
Pour des raisons analogues, on obtient:
-
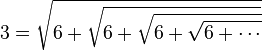
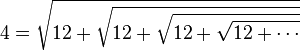
Si r est un entier strictement supérieur à 1,
Plus généralement, si p étant un nombre réel supérieur ou égal à 1,
Si p est égal à 1, on obtient le nombre d'or:
-
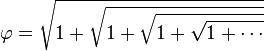
Le mathématicien Ramanujan obtint une formule alternative pour 3. Il partit de la décomposition
et construisit le produit n(n + p) en fixant p = 2
Il substitua le terme (n + 3)
Ramanujan réitéra à l’infini en remplaçant maintenant n par 1 sans se préoccupper du passage à la limite et obtint la jolie formule:
En fixant n et p à d’autres valeurs positives ou en élevant au carré une formule obtenue, on peut également construire d’autres belles formules comme:
En résumé, la relation suivante, itérée à l’infini:
permet donc d’exprimer tous les nombres entiers strictement supérieurs à 1 comme une itération infinie de racines carrées.
En particulier, en fixant n = 0 et toujours sans se préoccuper du passage à la limite
Le nombre π s’exprime sous la forme d’une itération infinie de racines carrées:
-
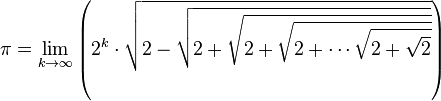
Ou encore:
Racines carrées des entiers de un à vingt
-
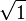
= 1 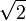
≈ 1,4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 78462 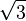
≈ 1,7320508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 16909 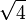
= 2 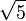
≈ 2,2360679774 9978969640 9173668731 2762354406 1835961152 5724270897 2454105209 25638 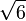
≈ 2,4494897427 8317809819 7284074705 8913919659 4748065667 0128432692 5672509603 77457 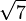
≈ 2,6457513110 6459059050 1615753639 2604257102 5918308245 0180368334 4592010688 23230 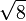
≈ 2,8284271247 4619009760 3377448419 3961571393 4375075389 6146353359 4759814649 56924 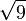
= 3 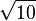
≈ 3,1622776601 6837933199 8893544432 7185337195 5513932521 6826857504 8527925944 38639 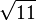
≈ 3,3166247903 5539984911 4932736670 6866839270 8854558935 3597058682 1461164846 42609 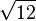
≈ 3,4641016151 3775458705 4892683011 7447338856 1050762076 1256111613 9589038660 33818 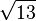
≈ 3,6055512754 6398929311 9221267470 4959462512 9657384524 6212710453 0562271669 48293 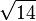
≈ 3,7416573867 7394138558 3748732316 5493017560 1980777872 6946303745 4673200351 56307 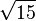
≈ 3,8729833462 0741688517 9265399782 3996108329 2170529159 0826587573 7661134830 91937 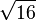
= 4 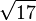
≈ 4,1231056256 1766054982 1409855974 0770251471 9922537362 0434398633 5730949543 46338 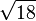
≈ 4,2426406871 1928514640 5066172629 0942357090 1562613084 4219530039 2139721974 35386 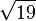
≈ 4,3588989435 4067355223 6981983859 6156591370 0392523244 4936890344 1381595573 28203 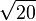
≈ 4,4721359549 9957939281 8347337462 5524708812 3671922305 1448541794 4908210418 51276
Nous remarquons, que seuls les carrés parfaits admettent pour racines carrées des rationnels.
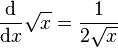
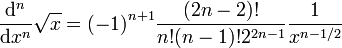
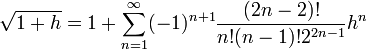
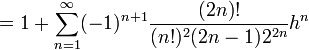
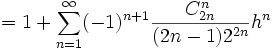
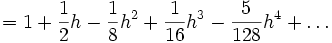
![{C_{2n}^n \over (2n-1)}=2\left[C_{2n-2}^{n-1}-C_{2n-2}^n \right]](https://static.techno-science.net/illustration/Definitions/autres/6/6a339bad9a07f7dc3d898e59fb3a9814_cc2617fb95b7ae43702798ca55c55525.png)
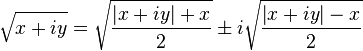
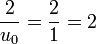
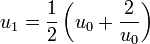
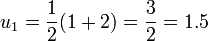
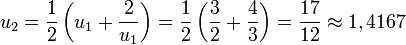
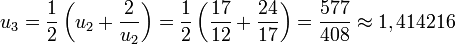
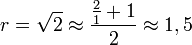
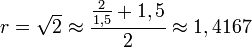
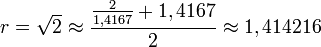
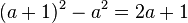
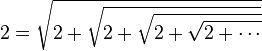
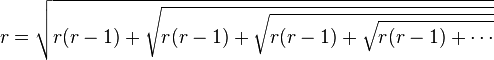
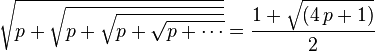
![(n+p)^2 = 1 + [n+(p-1)][n+(p+1)]\,](https://static.techno-science.net/illustration/Definitions/autres/d/d2b6141735aa5e63c004c2334fdd055e_b38326805d6cbd75be8037b5b9dff57f.png)