Équation diophantienne - Définition

Introduction

Une équation diophantienne, en mathématiques, est une équation dont les coefficients sont des nombres entiers et dont les solutions recherchées sont également entières. Le terme est aussi utilisé pour les équations à coefficients rationnels. Les questions de cette nature entrent dans une branche des mathématiques appelée arithmétique.

Si l'expression du problème posé est parfois simple, les méthodes de résolution peuvent devenir complexes. Carl Friedrich Gauss , un mathématicien du XIX^e siècle, disait des problèmes de cette nature : « Leur charme particulier vient de la simplicité des énoncés jointe à la difficulté des preuves. »

Certaines équations diophantiennes ont demandé pour leur résolution les efforts conjugués de nombreux mathématiciens sur plusieurs siècles. Gauss se plaignait « des efforts démesurés que lui a coûté la détermination d'un signe d'un radical dans la théorie des nombres ; bien d'autres choses ne l'ont pas retenu autant de jours que cette question l'a retenu d'années. » Le dernier théorème de Fermat est un exemple archétypal, il est conjecturé par Pierre de Fermat et résolu en 1994 par Andrew Wiles après 357 ans d'efforts de la part de nombreux mathématiciens.

L'intérêt de la résolution de questions de cette nature réside rarement dans l'établissement d'un théorème clé pour les mathématiques, la physique ou les applications industrielles, même s'il existe des contre exemples comme la cryptologie, qui fait grand usage du petit théorème de Fermat. Leur analyse amène le développement d'outils mathématiques puissants dont l'usage dépasse le cadre de l'arithmétique. Les formes quadratiques sont à cet égard exemplaires. La richesse et la beauté formelle des techniques issues de la résolution d’équations diophantiennes fait de l'arithmétique la branche reine des mathématiques pour David Hilbert.

Ce type d'équation doit son nom au mathématicien grec Diophante d'Alexandrie, un mathématicien vivant à une date incertaine, probablement autour du III^e siècle. Il est l'auteur d'un traité, Arithmétiques, étudiant des questions de cette nature.

Arithmétique élémentaire

Si les questions diophantiennes deviennent rapidement difficiles, il existe certaines exceptions résolubles avec un minimum d'outils théoriques et une démonstration courte et simple.

Identité de Bézout

• Articles détaillés : Équation diophantienne ax+by = c - Théorème de Bachet-Bézout

Quelques techniques élémentaires permettent de résoudre une première famille d'équations diophantiennes. Un exemple est donnée par l'équation linéaire du premier degré à deux indéterminées :

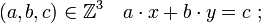
Cette équation porte le nom d'identité de Bézout, du nom du mathématicien qui a généralisé ce résultat aux polynômes. Sa résolution n'utilise que la division euclidienne et l'algorithme d'Euclide. Cette identité possède un double statut. Elle correspond à une équation diophantienne et représente un des piliers soutenant l'édifice de l'arithmétique élémentaire. Le lemme d'Euclide se démontre à l'aide de cette identité et le théorème fondamental de l'arithmétique à l'aide du lemme d'Euclide. Le théorème fondamental permet de déterminer les propriétés des opérateurs plus grand commun diviseur et plus petit commun multiple ainsi que celles des nombres premiers entre eux.

Théorème de Wilson

Un exemple d'équation diophantienne utilisant ces outils pour sa résolution est le théorème de Wilson. Il correspond à la résolution de l'équation suivante, le signe ! désignant la fonction factorielle :

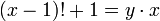
Les seules valeurs de x différentes de un vérifiant cette équation sont les nombres premiers.

Triplet pythagoricien

Le lemme d'Euclide permet de venir à bout de la recherche des triplets pythagoriciens, c'est-à-dire des triplets de nombres entiers (x, y, z) vérifiant l'équation :

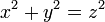
Ces mêmes techniques permettent de montrer que l'équation suivante, correspondant au dernier théorème de Fermat pour n égal à 4, n'a pas de solutions autres que celles qui vérifient x.y.z = 0. Cette équation diophantienne correspond à :

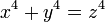
Petit théorème de Fermat

Pierre de Fermat consacre une large part de ses recherches mathématiques à la résolution de questions diophantiennes. Il découvre le petit théorème de Fermat qu'il exprime de la manière suivante : « Tout nombre premier mesure infailliblement une des puissances -1 de quelque progression que ce soit, et l'exposant de la dite puissance est sous-multiple du nombre premier donné -1 ... ». En terme diophantien, il offre une réponse partielle à l'équation suivante, où a désigne un entier et p un nombre premier :

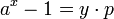
Le petit théorème de Fermat indique que p – 1 est une valeur possible pour x. Ce résultat possède de nombreuses applications. Il permet de construire des grands nombres premiers, comme ceux de Mersenne, correspondant à l'équation suivante où y est recherché parmi les nombres premiers :

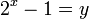
Il est relativement aisé de montrer que x est alors aussi un nombre premier. Cette question diophantienne permet de trouver les plus grands nombres premiers connus en 2008. Fermat s'intéresse à une équation analogue, permettant de construire d'autres nombres premiers portant maintenant son nom. Ici y est encore recherché dans les nombres premiers :

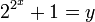
A cette occasion, Fermat commet la seule conjecture fausse connue de lui. Il imagine que tout nombre de Fermat est premier : « Si je puis une fois tenir la raison fondamentale que 3, 5, 7, 17, 257, 65537... sont nombres premiers, il me semble que je trouverai de très belles choses en cette matière, car j'ai déjà trouvé des choses merveilleuses dont je vous ferai part ». Presque un siècle s'écoule avant que Leonhard Euler présente un diviseur du cinquième nombre de Fermat. Il ne dévoile la construction de sa preuve que quinze ans plus tard. Elle correspond exactement aux travaux de Fermat, ayant permis de démontrer en 1640 la non primalité de deux nombres de Mersenne.

L'intérêt du petit théorème de Fermat ne se limite pas à l'étude de la primalité de nombres entiers. Il permet aussi de résoudre certaines équations, la suivante est un exemple où p désigne un nombre premier :

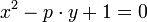
Elle correspond à une étape de la résolution de l'équation suivante :

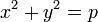
Si cette équation est résolue pour p premier, il devient relativement aisé de la résoudre pour p un entier positif quelconque. La résolution de cette équation se fonde sur un résultat nommé théorème des deux carrés de Fermat et dont la première preuve connue est l'œuvre d'Euler. Ce mathématicien généralise le petit théorème en apportant une réponse de même nature que celle de Fermat à l'équation suivante, ici a et b désignant deux entiers premiers entre eux :

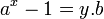
Ce résultat est connu sous le nom de théorème d'Euler.

Autres techniques

Joseph-Louis Lagrange cherche à généraliser des équations diophantiennes déjà traitées dans des cas particuliers. L'équation du théorème des deux carrés devient, si n désigne un entier sans facteur carré et p un nombre premier :

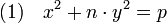
Pour cela, il étudie les formes quadratiques à deux variables, c'est-à-dire les fonctions φ qui à un couple (x, y) associe :

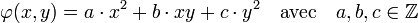
Il cherche à savoir quelle forme linéaire est équivalente à quelle autre. Equivalente signifie en termes modernes qu'un changement de base dans Z² (Z désigne l'ensemble des nombres entiers) permet de passer d'une forme à une autre. Cette démarche lui permet de résoudre l'équation (1) dans le cas où n est égal à 1, 2, 3 ou 5. Le cas général reste hors de portée.

Une autre généralisation de cette équation est résolue à l'aide de cette méthode, elle consiste à trouver le plus petit nombre de carrés nécessaire pour trouver au moins une solution pour tout entier positif. La réponse est 4, elle correspond à l'équation suivante :

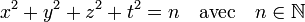
Le Théorème des quatre carrés de Lagrange affirme que pour toute valeur de n, cette équation admet une solution. Edward Waring généralise la question sous le nom de problème de Waring qui s'exprime de la manière suivante. Combien faut-il de termes dans une somme de puissance k^ième pour obtenir tous les entiers positifs ?

L'équation (1), pour une valeur donnée de n, impose de résoudre pour la même valeur du paramètre n et pour p un nombre premier quelconque, l'équation :

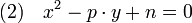
Pour chaque valeur de n, il est souvent relativement simple de trouver la liste des nombres premiers admettant une solution pour l'équation (2). L'expression de la solution générale est conjecturée par Euler, mais sa démonstration échappe aux arithméticiens du XVIII^e siècle.

Lagrange s'intéresse à une autre question, déjà soulevée par Fermat 150 ans plus tôt et par Diophante dans l'antiquité. Elle correspond à l'équation dite de Pell-Fermat. Si n est un entier sans facteur carré, elle s'écrit :

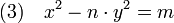
Cette question est objet d'étude par les mathématiciens indiens si m est égal à 1. La méthode dite de chakravala permet de trouver les solutions avec une grande efficacité. Bhāskara II l'utilise pour n égal à 61 et trouve la solution x = 1 766 319 049 et y = 226 153 980. Fermat redécouvre cette méthode et la démontre selon les critères de rigueur de l'époque. Lagrange trouve une autre méthode, fondée sur les fractions continues. Elle permet aussi de trouver une infinité de solutions pour toutes valeurs de n, la démonstration du fait que toutes les solutions sont bien atteintes pour m = +/-1 est enfin démontrée, le cas général reste néanmoins hors de portée.