Équation diophantienne - Définition

Théorie algébrique des nombres

Quatorze ans plus tard, le succès de Dirichlet est suivi par une tentative réussie de Gabriel Lamé pour résoudre le cas n égal à 7 du dernier théorème de Fermat. Une fois encore les techniques modulaire sont à l'œuvre, la structure clé est encore un anneau euclidien. Mais la complexité de la preuve montre que la démarche n'est pas généralisable.

Ainsi, l'arithmétique modulaire permet de véritables avancées, mais la résolution générale de famille d'équations reste très généralement hors de portée. Cette remarque est valable pour le dernier théorème de Fermat ainsi que pour les équations quadratiques. En effet, s'il est possible de trouver une infinité de solution à l'équation (3), personne ne sait démontrer si l'ensemble des solutions est exhaustif ou non. Enfin l'équation (1) reste inabordable dans le cas général. Une famille d'anneaux représentent des bons candidats pour aller plus loin, ils sont constitués d'entiers algébriques.

Entier algébrique

Cette figure illustre le groupe des unités de l'anneau des entiers de Dirichlet. Ici ω désigne l'entier de Dirichlet égal à 1/2.(1 + √5).

Plusieurs exemples d'anneau entiers algébriques ont déjà été observés dans cet article : les entiers de Gauss, d'Eisenstein ou de Dirichlet. Une démarche plus générale consiste à étudier un corps quadratique c'est-à-dire le plus petit sous-corps de C (l'ensemble des nombres complexes) contenant les racines d'un polynôme de degré deux. Un entier quadratique est un élément de ce corps qui est racine d'un polynôme unitaire (le monôme de degré deux a pour coefficient un) et à coefficients dans Z. Les entiers quadratiques forment un anneau inclus dans le corps quadratique.

A certains égards, les exemples utilisés sont exceptionnels. Dans le cas général, deux obstructions demandent d'aménager les résultats de l'arithmétique modulaire pour permettre de résoudre des équations diophantiennes. Une fois la structure de ces obstructions comprises, les équations de type (1) et (3) peuvent être traitées.

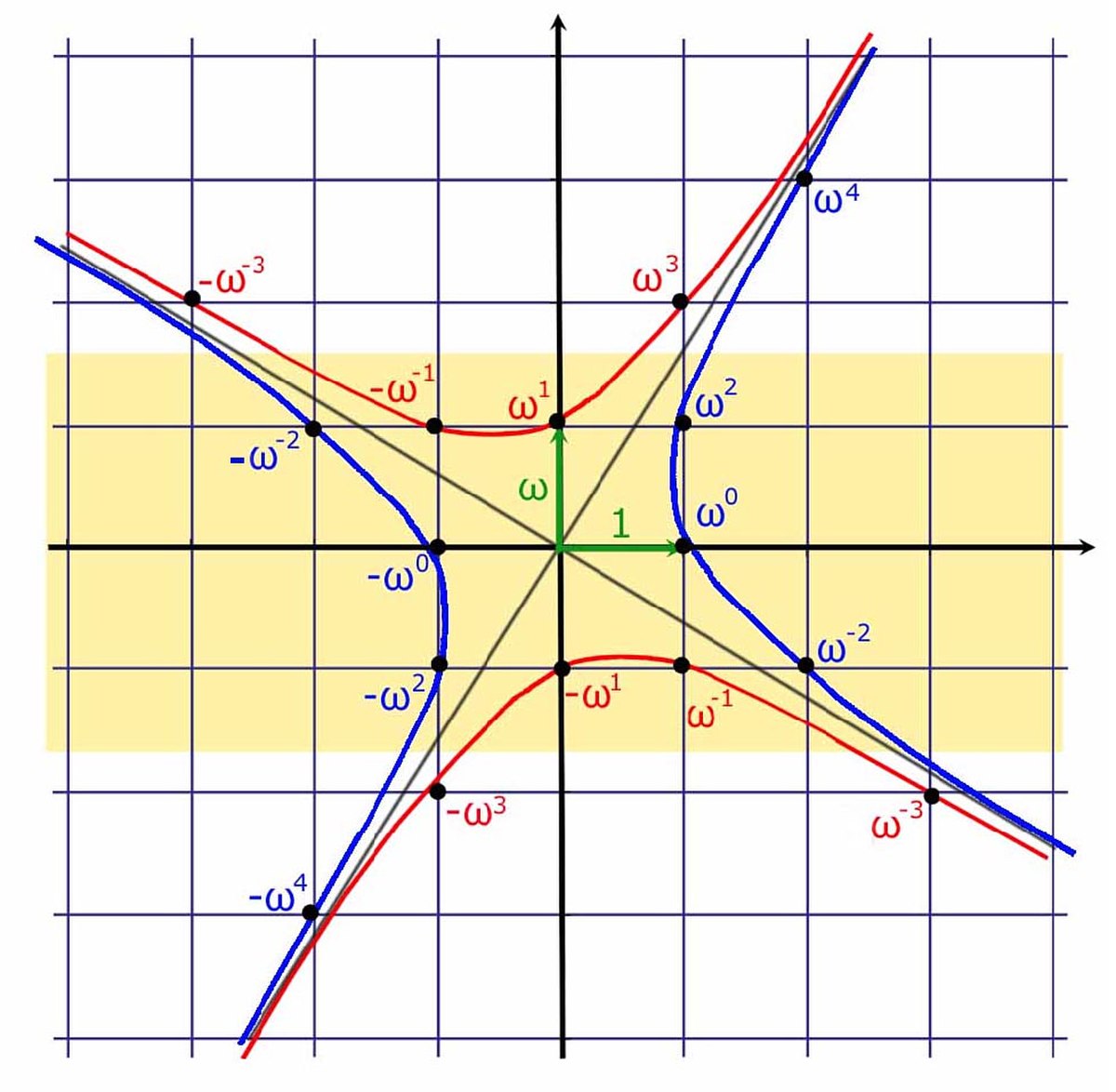
La première est mise à jour par Dirichlet. Pour les entiers quadratiques, elle ne concerne que les cas où les éléments sont tous inclus dans l'ensemble des nombres réels, on parle de corps quadratique totalement réel. Le groupe des unités, est l'ensemble des éléments inversibles de l'anneau. Il devient infini sur un corps quadratique totalement réel. L'équation (3) revient à trouver tous les éléments du groupe des unités de l'anneau. Le théorème des unités de Dirichlet donne la structure d'un tel groupe, sans se limiter aux extensions associées aux polynômes de degré deux. Dans le cas d'un corps quadratique totalement réel, il est isomorphe au groupe additif Z/2Z x Z. Graphiquement, l'illustration de gauche montre que les éléments se situent sur quatre branches d'hyperboles. Toute solution de l'équation de Pell-Fermat correspond à un couple de racines inverse l'une de l'autre. Les fractions continuées permettent de déterminer une racine primitive du groupe des unités, c'est-à-dire que cette racine génère toutes les autres. La compréhension de la structure de cette obstruction montre que la méthode de Lagrange permet effectivement de trouver toutes les solutions de l'équation (3) et clôt la question.

La deuxième obstruction concerne la décomposition en facteurs premiers d'un entier algébrique. Elle est unique dans le cas des anneaux euclidiens, principaux ou factoriels. Cette propriété, exprimée par le théorème fondamental de l'arithmétique, est l'un des fondements de l'arithmétique élémentaire ou modulaire. Elle n'est plus vérifiée dans le cas d'un anneau d'entiers algébriques. Ernst Kummer interprète cette réalité comme un défaut de nombres premiers, c'est parce qu'il en manque que l'unicité de la décomposition disparaît. Il a l'idée d'enrichir l'anneau de nombres idéaux pour remplacer les nombres premiers manquants. Richard Dedekind donne à cette théorie son formalisme moderne. Il met en évidence en 1876 que les nombres idéaux de Kummer se formalisent simplement à l'aide du concept d'idéal, un sous-groupe de l'anneau stable par multiplication par un élément quelconque. Il reprend à cette occasion le vocabulaire de Kummer, tout en modifiant le formalisme. Les nombres premiers idéaux correspondent en fait à des idéaux premiers non principaux. Grâce à la notion d'idéal fractionnaire, il trouve un équivalent du théorème fondamental : tout idéal se décompose de manière unique en un produit d'idéaux premiers. Il reste alors à déterminer la structure des idéaux premiers principaux et non principaux. À l'aide d'un groupe quotient d'idéaux par des idéaux principaux, il définit le théorème clé, à savoir que ce quotient, appelé groupe des classes d'idéaux est un groupe abélien fini. Dans les cas simples, comme celui des anneaux d'entiers quadratiques, ce résultat permet de déterminer les idéaux premiers non principaux et par la même occasion de résoudre l'équation (3) dans le cas général.

Corps cyclotomique

Ernst Kummer démontre en 1847 le dernier théorème de Fermat pour tout nombre premier régulier

Si le formalisme moderne venant à bout de la deuxième obstruction est l'œuvre de Dedekind et date de la fin du XIX^e siècle, une partie non négligeable du travail mathématiques provient des travaux de Kummer du milieu du siècle. Sa préoccupation est la généralisation de la loi de réciprocité quadratique ainsi que le dernier théorème de Fermat.

La démonstration du cas n égal à sept de Lamé se fonde encore sur l'anneau des entiers algébriques d'un corps quadratique. L'impossibilité de réponse générale fondée sur l'étude des entiers quadratiques poussent Lamé et Kummer à étudier d'autres corps de nombres, c'est-à-dire que plus petit sous-corps de C contenant toutes les racines d'un polynôme. Ils choisissent tous deux les polynômes cyclotomiques, c'est-à-dire les polynômes unitaires de degré minimal ayant pour racine une racine de l'unité. Le corps de nombre associé est appelé corps cyclotomique. De tels corps possèdent de multiple bonnes propriétés. Le polynôme cyclotomique est à coefficients dans Z ainsi une racine de l'unité est toujours un entier algébrique. Un corps cyclotomique reste plus longtemps principal et, si tel est le cas, l'anneau des entiers vérifie le théorème fondamental de l'arithmétique. Ainsi, les anneaux d'entiers algébriques des corps cyclotomiques d'indice 5, 7, 11, 13, 17 et 19 sont principaux. Cette observation pousse Lamé à présenter une solution qu'il croit générale au grand théorème de Fermat en 1847. Kummer est plus prudent, il a déjà démontré trois ans plus tôt que pour l'indice 23, l'anneau n'est pas principal.

Le formalisme utilisé dans cet article est celui en vigueur actuellement et diffère de celui de Kummer, cependant le contenu mathématique est le même. La difficulté à résoudre est de comprendre comment s'agencent les idéaux premiers non principaux. Ce problème, bien que résolu plus tôt, est finalement plus complexe que celui des anneaux d'entiers quadratiques. Le polynôme à l'origine du corps de nombres est de degré quelconque et non plus égal à deux. La théorie de Galois est d'une grande aide. Dans le cas d'un corps cyclotomique K, l'extension est dite galoisienne, c'est-à-dire qu'il existe autant d'automorphismes de K que l'ensemble possède de dimensions s'il est considéré comme un Q espace vectoriel. Ces automorphismes forment un groupe fini G, appelé groupe de Galois. L'image d'un idéal premier par un automorphisme est aussi un idéal premier. Cette remarque permet de comprendre la structure des idéaux premier à l'aide de la ramification. Tout idéal premier P contient un unique nombre premier p. La technique consiste alors à décomposer l'idéal principal pK en idéaux premiers. Le groupe G agit transitivement sur le idéaux premiers décomposant pK ce qui permet de déterminer la décomposition des idéaux premiers dans les extensions galoisiennes.

De plus, K est une extension abélienne et même cyclique, c'est-à-dire que le groupe de Galois est cyclique. Une conséquence est que le groupe des classes est aussi cyclique. Le groupe des classes devient relativement aisé à déterminer et, si p est un nombre premier régulier, alors il ne divise pas l'ordre du groupe des classes. Cette propriété permet d'obtenir une démonstration relativement aisée du dernier théorème de Fermat. Les seules exceptions plus petites que 100 sont 37, 59 et 67.