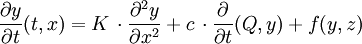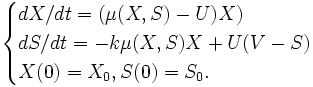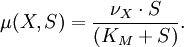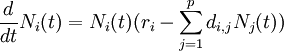Biomathématique - Définition
La biomathématique sous entend l'association de deux sciences : la biologie et les mathématiques. De façon précise les biomathématiques sont constituées par l'ensemble des méthodes et techniques mathématiques, numériques et informatiques qui permettent d'étudier et de modéliser les phénomènes et processus biologiques. Il s'agit donc bien d'une science fortement pluridisciplinaire que le mathématicien seul (ou le biologiste seul) est incapable de développer. Pour naître et vivre cette discipline exige des équipes interdisciplinaires mues par le sens du concret. L'abstrait n'est qu'un moyen pour parvenir à une meilleure compréhension des phénomènes biologiques. Les biomathématiques ont des débouchés tant pratiques que théoriques dans de nombreux domaines comme la biologie des populations, la physiologie, la génomique, la pharmacologie etc.
Modèle en biomathématiques
Un modèle est un système d'équations mathématiques rendant compte de toutes les données expérimentales connues du phénomène biologique étudié. Le modèle permet entre autres :
- de mieux comprendre un processus biologique ;
- d'agir sur le système de façon optimale.
En analogie à un système thermodynamique, on distingue les variables d'état, qui décrivent l'évolution du système, et les variables de contrôle, sur lesquelles il est possible d'agir. Il existe de ce fait deux grands types de modèles :
- Les modèles cognitifs où les équations sont obtenues en traduisant les lois physiques auxquelles obéit le système (par exemple modélisation des réactions métaboliques (lien) ; modélisation de la dynamique intracrânienne du liquide céphalo-rachidien (lien)) ;
- Les modèles de simulation qui ignorent les mécanismes physiques sous-jacents et qui proposent a priori des équations dont il faut ajuster les variables aux données expérimentales (par exemple : simulation de la dynamique des rétrovirus et leur résistance au traitement. (lien))
Les modèles de connaissance sont plus satisfaisants car ils tiennent compte de la physico-chimie du système. Ils exigent que le phénomène soit parfaitement connu et que les lois physiques auxquelles le processus obéit soient bien quantifiées. En revanche les modèles de simulation sont moins exigeants. Ils relient l'entrée à la sortie du système à partir de données expérimentales.
On a cependant souvent affaire à des modèles intermédiaires. Dans la pratique on rencontre de nombreux modèles différents censés représenter le même système biologique. Se pose alors la question de l'unicité des modèles. Tout modèle qui satisfait les données expérimentales est considéré comme convenable. Les modèles diffèrent par les approximations, le type et le nombre de paramètres pris au départ. On a intérêt à considérer, en fonction d'un objectif précis, le modèle le plus simple, qui sera traduit par le système d'équations le plus facile à manipuler et à traiter. La seconde contrainte à imposer à un modèle est son utilité : cet outil est destiné du point de vue des biologistes à mettre en évidence des résultats expérimentaux, à justifier une hypothèse ou à optimiser un système de production etc.
Pratiquement tout phénomène est modélisable avec plus au moins de difficultés selon les données disponibles. Grâce aux méthodes d'approximation le modèle peut se ramener à un système :
- d'équations algébriques (linéaires ou non linéaires) ;
- d'équations différentielles, intégrales ou à dérivées partielles.
Techniques de modélisation
Bien que chaque système biologique requière ses propres techniques de modélisation, il existe des méthodes de modélisation très générales et fort utiles que nous allons passer en revue.
Analyse compartimentale
Cette technique de modélisation convient très bien aux systèmes de transformations chimiques et d'échanges cellulaires. On peut néanmoins l'étendre à bien d'autres circonstances. Plusieurs étapes sont nécessaires pour élaborer un modèle compartimental.
- définir la substance à étudier et ses transformés dans les différents compartiments (qui sont en fait des classes d'équivalence);
- déterminer par l'observation les constantes de proportionnalité d'échange entre les compartiments ;
- faire le bilan de masse (débit entrant – débit sortant) à l'aide d'un système différentiel linéaire ;
- faire les approximations nécessaires pour simplifier la résolution numérique.
Les biologistes utilisent largement cette méthode pour l'analyse quantitative des flux métaboliques, de la diffusion des marqueurs et des médicaments en pharmacocinétique (lien).
Modèle de diffusion, convection, réaction
De nombreux systèmes biologiques sont constitués d'interaction entre deux ou plusieurs substances. Si l'on modélise l'évolution au cours du temps et dans l'espace, des concentrations ou des pressions partielles de ces substances on est conduit à des systèmes aux dérivées partielles. Dans le cas d'une dimension de l'espace x on obtient des EDP du type :
où y et z sont les concentration de deux substances, K est une constante de diffusion, c est la constante de convection ou de transport, Q est le débit de convection et f est une fonction donnée qui décrit l'interaction entre les deux substances.
Des relations supplémentaires qui émanent de l'observation (conditions initiales et limites) sont nécessaires pour assurer l'unicité de la solution. On utilise concrètement ce modèle pour l'étude quantitative des échanges gazeux respiratoires entre les alvéoles et les capillaires sanguins. (lien).
Modèles stochastiques
- Modèle stochastique en écologie (lien)

- Modélisation stochastique du rythme circadien (lien)

Exemples de modèles biomathématiques
Croissance bactérienne
Pour modéliser l’évolution d’une colonie bactérienne, on a souvent recourt au système d’équations différentielles de Cherruault[1] (1998) :
- k est une constante d’échanges identifiée par les données expérimentales ;
- X et S sont respectivement la concentration de la biomasse et du substrat dans le milieu nutritif ;
- V est l’entrée de substrat ;
- U(t) est une fonction de contrôle (qui peut correspondre p. ex. à la concentration de l’éthanol dans un processus de fermentation alcoolique) ;
- µ(t) est une fonction non linéaire qui définit l’échange entre le compartiment bactérien X et le milieu de culture S. Cette fonction est calculée selon la loi de Monod, qui a pour expression :
Ici KM est la constante de Michaelis et νX une constante expérimentale.
Dynamique des populations
La dynamique des populations a été traditionnellement un domaine de prédilection en biomathématiques. Des modèles décrivant l'évolution des populations ont fait l'objet de plusieurs études qui datent du XIXe siècle. Entre autres, les fameuses équations de Lotka-Volterra (1925) permettent de modéliser l’évolution au cours du temps des proies et des prédateurs dans un écosystème. On les appelle quelquefois modèles “proies-prédateurs”, la formule générale est :
- Ni est le nombre d’individus de l’espèce (i), avec N0 l'effectif initial ;
- p est le nombre d’espèces en compétition ;
- ri est le taux de croissance spécifique de l’espèce (i) ;
- di,j sont les coefficients qui mesurent l’ampleur avec laquelle la présence d'une l’espèce (j) affecte la survie de l’espèce (i).
Organisation spatiale et morphogenèse
Le mathématicien anglais Alan Turing, a cherché à jeter les bases mathématiques d'une théorie de la morphogénèse. Dans un article publié en 1952, intitulé : The chemical basis of morphogenesis[2], il a montré comment une réaction chimique couplée à un phénomène de diffusion pouvait conduire à des distributions périodiques dans l'espace des concentrations de certaines espèces chimiques. Selon Turing, un système de substances chimiques appelées "morphogènes" réagissant ensemble et diffusant à travers les tissus rend adéquatement compte du phénomène principal de morphogenèse. À condition toutefois que des interactions entre réactions chimiques aient lieu avec autocatalyse, rétroaction, échanges croisés etc. et donnent lieu à des processus non linéaires avec rupture de symétrie[3].
Maladies infectieuses
Le système mixte de Marchuk (1994)[4] est l'un des modèles les plus courants qui décrivent l’évolution d’une maladie infectieuse d'origine virale. Il prend en considération les réactions de défense de l’organisme qui sont traduites par des équations mathématiques. Ce modèle permet d’expliquer les caractéristiques fonctionnelles du système immunitaire ainsi que le rôle de la température, le mécanisme de la réponse immunitaire, la nature de l'agent viral etc. (lien)

Importance
Il y a longtemps que les scientifiques appliquent les mathématiques à la biologie, mais ce n'est que récemment qu'il y a eu un tel essor, pour différentes raisons :
- L'explosion de la masse de données dues à la révolution de la génomique, qui est difficile à exploiter sans l'utilisation d'outils analytiques.
- Le récent développement d'outils comme la théorie du chaos pour aider à comprendre les mécanismes complexes et non-linéaires en biologie.
- L'énorme croissance des capacités de calcul, donc de simulation, des nouveaux ordinateurs.
- Un intérêt croissant des expériences in silico sur la recherche humaine et animale.
Recherches
La suite est une liste des différentes voies de recherche en biomathématiques.
Modélisation cellulaire et biologie moléculaire
Ce domaine a reçu un important élan grâce au développement de la biologie moléculaire.
- Modélisation des neurones et des agents cancérigènes.
- Mécanique des tissus biologiques.
- Enzymologie et cinétique enzymatique.
- Modélisation et simulation du cancer.
- Modélisation de l'interaction entre des populations de cellules en mouvement.
- Modélisation mathématique de la formation de cicatrices dans les tissus.
- Modélisation mathématique de la dynamique intracellulaire.
La modélisation est normalement faite avec une ou plusieurs équations différentielles ordinaires (EDO). Dans la plupart des cas, de tels systèmes d'EDO peuvent être résolus, de manière analytique ou numérique. Une méthode populaire pour résoudre numériquement les EDO est l'algorithme Runge-Kutta.
La modélisation stochastique est plus compliquée et utilise l'algorithme Gillespie. L'algorithme Gillespie est normalement utilisé pour simuler un petit nombre de systèmes chimiques (comme 100 copies d'un ARNm, de protéines, ou de ribosomes). Cet algorithme simule exactement un échantillon de la solution de l'équation chimique générale.
Modélisation de systèmes physiologiques
- Modélisation des maladies cardiovasculaires
- Modélisation du cœur à plusieurs échelles
Modélisation dans l'espace
Un travail intéressant dans ce domaine est celui d'Alain Turing dans son article sur la morphogenèse intitulé The chemical Basis of Morphogenesis, publié en 1952.
- Le comportement en essaims.
- La théorie chimico-mécanique de la morphogenèse.
- La formation de patrons biologiques.
Ces exemples sont caractérisés par des mécanismes complexes et non-linéaires, et il est devenu clair que leur compréhension ne peut être entière qu'avec des modèles mathématiques. De par la grande diversité des thèmes, la recherche en biomathématiques est souvent faite en collaboration avec des mathématiciens, des physiciens, des biologistes, des médecins, des zoologistes, des chimistes, etc.