Détermination de la constante de Hubble - Définition

Introduction

La constante de Hubble quantifie l’accélération (ou la récession) de l’expansion de l’univers.

Introduction

Edwin Hubble est l’un des plus importants astrophysiciens du début du XX^e siècle. Outre une constante qui porte son nom, il a créé aussi avec Arthur Eddington une classification des galaxies encore utilisée aujourd’hui. La constante de Hubble quantifie l’accélération (ou la récession) de l’expansion de l’univers. Elle est directement liée à la constante cosmologique introduite par Einstein dans la relativité générale qui permet de modéliser l’univers. La constante d’expansion de l’univers permet, entre autres, de déterminer l’âge de l’univers, via deux constantes Ω_m l’énergie de la matière et Ω_Λ la densité énergétique du vide. La constante de Hubble permet aussi de déterminer la taille de l’univers observable (R_obs =ct), le coefficient de courbure ( ) ainsi que la densité des éléments lumineux (H,D,3He,4He,…) créés après le big-bang. La constante de Hubble a été très difficile à mesurer dans le passé, et de nombreux problèmes ont été sous-estimés ou ignorés.

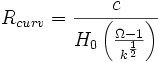
La constante de Hubble se formule d’une manière très simple : H₀= où v est la vitesse radiale, elle se mesure en . Ce sujet est à traiter de manière à comprendre les différents procédés physiques, puis les principaux indicateurs de la constante d’expansion de l’univers. Le véritable enjeu des différents systèmes de détermination de H₀ est l’incertitude du résultat. En effet les différents systèmes ont chacun leur propre précision. Il convient d'étudier lesquels sont les plus efficaces et lesquels sont les plus simples d’utilisation.

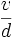
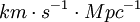
Travaux récents

La constante d’expansion de Hubble est un facteur important dans la compréhension de l’évolution, de la forme et de l’âge de l’univers. Depuis maintenant plusieurs dizaines d’années, les chercheurs s'efforcent de déterminer cette constante le plus précisément possible, et parfois à partir de peu de moyens, notamment au début dans les années 1930. L’observation a été la base des théories jusqu'à récemment, où les mathématiciens et les physiciens essaient de comprendre grâce aux modèles numériques le fonctionnement de l’univers, et les observations ne servent maintenant qu’à affirmer ou infirmer les théories, et ce grâce notamment au télescope spatial. En effet, il est possible aujourd’hui de voir l’univers primitif ou presque, ce qui nous permet d’affiner les différentes hypothèses.

Afin de déterminer la constante d’expansion de l’univers, il faut choisir un élément dans l’Univers qui soit suffisamment loin pour que l’effet de l’expansion soit visible par son spectre, et dont on comprenne le fonctionnement interne : luminosité, situation dans la galaxie, âge, etc. Plusieurs candidats se proposent aux chercheurs, chacun avec ses qualités et ses défauts. Les céphéides et les supernovae de type Ia ont été choisies. Pour comprendre ce choix, il faut étudier comment ces objets du ciel profond fonctionnent, les différentes observations qui ont été faites (et donc les différents résultats qui en découlent), les résultats et leur application en cosmologie.

La cosmologie

Les constantes Ω et Λ, base de la cosmologie

Il est important de parler d'abord des constantes ΩM et ΩΛ, très importantes en cosmologie, car elles déterminent, avec H0, l’âge de l’univers, sa courbure et d’autres paramètres essentiels pour toutes observations et pour tous calculs. Le paramètre de densité de matière dans l’univers ΩM est un paramètre sans dimension car Ω=ρ/ρc. L’effet de la matière se traduit toujours par un effet gravitationnel qui tend à refermer l’univers sur lui-même. Il existe une valeur critique ρc (correspondant à 1 atome d’hydrogène par m3, soit ρc= (3H0²)/ (8πG)) qui définit le mouvement de l’univers. En effet si ρ>ρc l’univers s’effondrera sur lui-même (Big Crunch). Si ρ=ρc l’univers est en équilibre et si ρ<ρc l’univers sera en constante expansion. De plus, ΩM, égal à ρ/ρc, définit la courbure de l’univers selon la relativité générale d’Einstein. Soit ΩM >1, et l’espace a une courbure positive, c’est-à-dire qu’on a un univers fermé et donc une géométrie sphérique. Soit ΩM < 1, et l’espace a une courbure négative, on dit alors que l’on a un univers ouvert et donc une géométrie hyperbolique. Soit ΩM =1, et l’espace a une courbure nulle, on est donc face à un univers plat et donc à une géométrie euclidienne.

La constante cosmologique Λ est un paramètre purement géométrique. Selon la théorie de la relativité générale, toute matière est énergie, toute force gravitationnelle a pour source une énergie. Or, Λ est une « constante », l’énergie qui lui est associée opère donc quels que soient le temps et la position. De plus, Λ engendre une force qui opère même en l’absence totale de matière et de rayonnement, donc sa source est une énergie résidant dans l’espace vide. Ce sont ces particules virtuelles qui surgissent du néant et y retournent sans que personne ne puisse les mesurer directement. Mais leurs effets sont mesurables (effet Casimir).

On a démontré qu’en fait Λ est une énergie répulsive, ce qui perturbe notre précédente théorie sur l’évolution. En effet, la densité totale de l’univers ρ n’est plus simplement ρM mais c’est ρM plus la densité d’énergie associée à Λ. Par conséquent Ω = ΩM +ΩΛ, ce qui complique considérablement le problème. En effet il se peut maintenant que l’univers soit en constante expansion sans être forcément ouvert !

Avec ces deux constantes, il serait possible de déterminer si l’univers est en expansion ou pas. En effet, si H0 n’existait pas, cela serait très simple : soit ΩM >ΩΛ ce qui signifierait que l’Univers s’effondre sur lui-même, soit ΩM=ΩΛ=0.5 et l’univers n’a ni expansion ni récession, soit ΩM<ΩΛ et l’univers est en constante expansion. Il est donc nécessaire de fixer une valeur de ces constantes avant de conclure. Dans la figure 1 figurent les résultats obtenus par le Supernovae Cosmology Project. Il semble évident que ΩΛ>ΩM (ΩΛ=0.7 et ΩM=0.3), ce qui signifierait que l’Univers est expansion.

Figure 1

(figure à venir)

Les étalons de la cosmologie.

Plusieurs choix étaient donnés aux chercheurs quant à leur observation et leur détermination de la constante d’Hubble : les quasars, les lentilles gravitationnelles… mais ils se sont arrêtés sur les supernovae de type Ia et les céphéides. Il est essentiel de bien expliquer leur choix afin de comprendre la complexité de cette constante et l’importance des étalons.

La constante d’Hubble se mesure en km/s/Mpc, et est une constante ce qui signifie qu’elle ne dépend ni du temps, ni de sa position. Si par exemple on a H0=50 km/s/Mpc, cela exprime le fait qu’un cube ayant un parsec de côté se développe de 50 km toutes les secondes dans les trois directions de l’espace. Donc quel que soit notre point de vue, tout ce qui nous entoure semble s’éloigner, si évidemment on fait abstraction de la force de gravitation. Or ce qui est à proximité est soumis à la gravitation (les planètes du système solaire sont attirées par le Soleil, qui est lui-même attiré au centre de la galaxie). Il faut donc regarder les objets beaucoup plus lointains pour que la gravitation soit minime par rapport à H0 (car plus l’objet est loin, plus vite il s’éloigne). De plus afin de voir la vitesse radiale de l’objet sur son spectre, il faut que celle-ci soit assez importante (i.e >5000Km/s). Donc pour résumer, plus l’objet étudié est loin, plus il est intéressant. C’est pourquoi les chercheurs se sont essentiellement intéressés aux supernovae de type Ia et aux céphéides (les supernovae de type Ia sont visibles à des distances proches de 400 Mpc, les céphéides sont quant à elles visibles jusqu’à près de 40 Mpc).

On pourrait se demander alors pourquoi ne pas utiliser les quasars qui sont les objets les plus lointains jamais observés, mais le fait que ces objets soient lointains ne fait pas forcément d’eux de bons indicateurs pour H0. En effet, comme nous allons le voir plus loin, il est important de bien comprendre le fonctionnement des objets que l’on étudie, or les quasars sont de véritables énigmes pour les scientifiques contrairement aux SnIa et aux céphéides qui ont été longuement étudiés par les chercheurs.

La plus récente mesure et la plus précise mesure de la constante d’Hubble ont été réalisées grâce au télescope spatial, et ont été dirigées par l’équipe de Wendy L. Freedman; ce fut le Hubble Space Telescope KEY PROJECT. Les résultats, les graphiques, les mesures sont tirées principalement des résultats qui datent de l’année 2000. Le HST Key Project a été une longue étude basée sur l’observation de 31 céphéides et de 36 supernovae de type Ia, entre autres. La liste des céphéides et des supernovae étudiées se trouve dans les feuilles 1 et 2 de l’annexe.

Qui sont-ils ?

Afin de pouvoir déterminer H0, il est nécessaire de bien comprendre le fonctionnement des objets que nous étudions, c’est-à-dire les supernovae et les Céphéides. Il convient désormais d'étudier comment fonctionnent ces « étoiles » et comment elles sont étudiées dans le cadre de la recherche de la constante d’Hubble.

Les supernovae de type Ia

Les supernovae de type I sont le résultat d’un système binaire serré, dans lequel l’une des deux étoiles est de faible masse et est dégénérée : c’est une naine blanche. Lorsque le compagnon, une étoile géante, est trop proche de la naine blanche et que son enveloppe extérieure dépasse son lobe de Roche, l’étoile perd sa masse par l’intermédiaire du point de Lagrange (figure2) et la masse de la naine blanche s’accroît alors jusqu’à dépasser la masse critique de Chandrasekhar (1.4 MSOLEIL). À ce stade, la masse de l’étoile est trop importante, et elle s’effondre sur elle-même, la force électromagnétique ne pouvant contrecarrer la force gravitationnelle à l’intérieur de l’étoile. Survient alors une très forte explosion thermonucléaire visible dans tout le cosmos (figure3).

Figure 2 : le lobe de Roche.

       (figure à venir)       

Explication sur le lobe de Roche. www.astro.psu.edu/users/rbc/a1/lec12a.htlm

Figure 3 : formation d’une supernova.

       (figure à venir)       

Plusieurs images détaillant par étapes la formation d’une SNIa. www.astro.psu.edu/users/rbc/a1/lec12a.html

Lorsqu’une supernova de type II atteint la masse critique de 1.4 MSOLEIL, elle crée une étoile à neutron. Les supernovae de type I et celles de type II sont différentes dans le fait que les premières n’ont pas d’hydrogène dans leur spectre, mais des éléments lourds. Les SNI sont donc plus âgées que les SNII. De plus, les SNIa sont un cas particulier des SNI : il existe du silicium dans leur spectre, contrairement aux SNIb et SNIc.

Il est nécessaire de bien comprendre le fonctionnement de l’objet observé. Les SNIa font partie de ces objets que les astronomes connaissent bien, car ils les ont longuement étudiés.

Les Céphéides

Les céphéides sont des étoiles jeunes, brillantes, dont l’atmosphère pulse d’une manière régulière d’une période allant de 2 à 100 jours. Elles se trouvent en abondance tout proche des galaxies spirales et écliptiques. Depuis les années 1920, le problème de la distance des objets extragalactiques (étoiles, nébuleuses, …) s’est posé aux astrophysiciens. Malgré les progrès de la technique et l’amélioration des télescopes, une mesure précise n’a jamais pu être réalisée. Avec le H0 Key Project, le télescope spatial a permis de découvrir une classe d’étoiles dont le fonctionnement est tout à fait compris des astronomes : les céphéides. La pulsation de leur enveloppe externe est facilement explicable car elle est due au mécanisme thermodynamique du même type que celui produit par une soupape d’un moteur. C’est-à-dire que l’hélium est recyclé de l’état d’une ionisation simple à un état d’une ionisation double, ce qui augmente la compression et a fortiori l’opacité.

Les théories physiques et la méthode de détermination d’H0

Le télescope Hubble est un outil formidable pour les astronomes, car il permet d’observer le ciel profond sans les turbulences de l’atmosphère, les nuages, le jour et la nuit. Mais il ne permet d’expliquer ce que l’on voit, il ne donne que les images et ce sont aux théoriciens de comprendre et d’essayer de déchiffrer les images et leur signification. À l’aide d’outils mathématiques, physiques et thermodynamiques puissants, ils peuvent comprendre le fonctionnement d’étoiles distantes de dizaines de millions de kilomètres.

Les théories physiques

Il est indubitablement essentiel de comprendre le fonctionnement de l’objet que l’on étudie et que l’on observe, et il est essentiel de bien s’en rendre compte. En effet il est difficile de déduire une distance d’un objet que l’on voit et que l’on ne connaît pas, car la distance est déduite de la luminosité, qui est elle-même en corrélation avec l’âge, la taille ou l’environnement dans lequel se trouve l’objet. Pour les SNIa, il existe une théorie qui relie la distance de l’astre et son pic de luminosité. Cet indicateur de distance est sans aucun doute le plus efficace, de plus il offre la meilleure précision pour des objets lointains, car c’est celui qui a la plus petite échelle de tous les indicateurs que nous ayons pour ces distances. Cette méthode est possible grâce aux télescopes terrestres et à leur foyer grand champ qui leur permet de produire une image couvrant la surface de la Lune et contenant près de 5000 galaxies pour une exposition de 10 minutes. Le principe est de regarder une partie du ciel à quelques jours voire quelques semaines d’intervalle afin de voir une variation de luminosité dans les galaxies lointaines (Figure 4). Un tel intervalle (une semaine) permet de voir l’intensification de luminosité propre à une supernovae, tout en évitant de dépasser son pic de luminosité, ce qui permet de suivre l’évolution de l’étoile pendant quelques mois et ainsi de déterminer son maximum de lumière nécessaire pour décomposer la lumière en ses composantes spectrales et ainsi avoir sa distance (Figure5).

Figure 4 : observation d’une supernova.

       (figure à venir)       

Images avant et après une explosion d’une SNIa d’un important décalage vers le rouge, prises par l’équipe du « High-z Supernova Search » en 1999. www.lrz-muenchen.de/projekte/hrlb-projects/webpages/h007z/

Figure 5 : courbe de luminosité.

       (figure à venir)       

Exemple de courbe de luminosité d’une SNIa. Reiss et al.: Evidence of an expending universe No.3 1998 (1033, fig.12).

Les avantages des céphéides sont nombreux : elles sont brillantes et ce sont des étoiles relativement jeunes qui se trouvent en abondance dans les galaxies spirales (de même type que la Voie Lactée). Leur abondance et leur courbe de lumière si particulière en font des objets facilement observables. De plus, leur temps de vie est assez long, car elles sont jeunes, ce qui permet de les observer longtemps et dans différentes longueurs d’onde (contrairement aux supernovae). Tout comme les supernovae de type Ia, leur échelle est assez petite, ce qui leur permet d’avoir une précision de l’ordre de 0.1 mag (Udalski et al.1999). La méthode la plus fréquemment utilisée pour déterminer la distance des galaxies proches est la relation période-luminosité (period-luminosity relation, PL relation). Basée sur la composition chimique des céphéides, cette méthode de détermination est très efficace. Mais, il existe plusieurs problèmes quant à leur observation, comme par exemple le fait que les céphéides étant des étoiles jeunes, elles se trouvent souvent dans un environnement riche en poussière interstellaire qui absorbe la lumière et à tendance à la rougir, ce qui fausse les données. Ou bien encore le fait que les céphéides des galaxies distantes de plus de 30Mpc sont difficilement décelables (phénomène d’entassement, le pouvoir séparateur des télescopes diminuant avec la distance d’observation).

Les mesures de la constante d’expansion de l’univers

De nombreuses équations existent sur la magnitude des céphéides, leur composition chimique et leur distance. Avec le Key Project, l’équipe de W.L. Freedman a réussi à donner des équations plus ou moins complexes à partir des données préexistantes (notamment les données de Udalski et al.). Les magnitudes visuelles et absolues à partir de PL relation et la distance ont été choisies comme étant : MV= -2.760[±0.03] (logP-1)-4.218[±0.02] avec σV = ±0.16 Les termes entre crochets MI= -2.962[±0.02] (logP-1) -4.904[±0.01] avec σI = ±0.11 sont les incertitudes. μ0 = W + 3.255[±0.02] (logP -1) +5.899[±0.01] avec σW= ±0.08 L’incertitude σ s’exprime en pourcentage. P : la période de rotation ; W : index de libre rougissement. Grâce à cela, il a été facile de déterminer leur distance et donc leur vitesse (figure 6).

Figure 6 : graphe distance/vitesse des galaxies avec céphéides.

              (figure à venir)       

Les vitesses ont été corrigées en utilisant le modèle décrit dans Mould et al. (2000a). W.L. Freedman : Final results from the Hubble Space telescope Key Project to measure the Hubble constant. 2001 (55)

On remarque que pour ces galaxies, H0=75 ± 10 km.s-1.Mpc-1. Les céphéides permettent de déterminer la distance des galaxies auxquelles elles appartiennent. Associée aux relations qui permettent de déterminer la distance des galaxies (Tully-Fischer, fondamental plane), cette méthode est excellente car d’une certitude maximale. Pour les supernovae de type Ia, le problème a été de déterminer quelles supernovae pouvaient être étudiées sans compromettre la précision des données, c’est-à-dire choisir les supernovae dont nous connaissions exactement la distance. L’équipe de W.L.Freedman est partie de l’échantillon de Gibson et al. (2000a), lui-même basé sur les études de Hamuy et al. (1996) et de Riess et al. (1998) dont les données comptaient 35 supernovae. Gibson a réduit le nombre des supernovae pour ces études à 29, auxquelles l’équipe de W.L.Freedman en a ajouté 21 autres. Ce sont donc au total 50 supernovae qui ont été utilisées pour déterminer la constante d’expansion de l’univers. Sur cet échantillon, il a été nécessaire d’en enlever quelques-unes dans le but d’affiner le résultat ; c’est pour cela qu’ils ont décidé de porter leur étude sur 36 supernovae ayant 3.5 < log (cz) CMB < 4.5et dont le pic de la magnitude de couleur │Bmax ─ Vmax │ < 0.20 (Schéma3, Annexe). Le résultat sur la constante d’Hubble associé avec le point zéro affecté de la correction sur la distance des céphéides (en appliquant une correction sur les composés chimiques internes de -0.2± 0.2mag dex-1, où un dex signifie un facteur de 10 dans la différence chimique) sur NGC 4639, 4536, 3627, 3368, 5253, et IC 4182 (cf. Schéma2, Annexe) nous donne une valeur finale de H0=71± 2 ± 6 km.s-1.Mpc-1. Pour les différents résultats sur les supernovae, se référer au schéma 1 de l’Annexe.

Les autres méthodes et les résultats

Les autres méthodes utilisées par l’équipe de W.L.Freedman pour la détermination de la constante d’expansion de l’univers sont basées sur la relation Tully-Fisher (galaxies), la fluctuation de la brillance de la surface des galaxies, l’étude des supernovae de type II et «  fundamental plane » (Figure 7). Grâce à toutes ces mesures, l’équipe de W.L.Freedman a pu donner un résultat très précis de H0=72 ± 8 km.s-1.Mpc-1.

Figure 7 : Récapitulatif des différents résultats pour H0 (figure à venir)

Références :(1) Hamyu et al. 1998;(2) Riess et al.1998;(3) Jha et al. 1999;(4) Gibson et al. 2000a;(5) Giovanelli et al.1997;(6) Aaronson et al.1982, 1986; (7) Sakai et al. 2000;(8) Jorgensen et al.1996;(9) Kelson et al. 2000;(10) Lauer et al.1998;(11) Ferrarese et al.2000a;(12) Scmidt et al. 1994 W.L. Freedman: Final results from the HST Key Project to measure the Hubble constant. 2001 (61)

Conclusion

L’équipe de W.L.Freedman a réalisé un travail incroyablement important pour la cosmologie, confirmant en effet par l’observation les différentes théories donnant H0 égale à ~70 km.s-1.Mpc-1 ce qui, ajouté à l’hypothèse vue au début, que ΩΛ=0.7 et ΩM=0.3, donne une expansion de l’univers âgée de 12.5 milliards d’années pour un univers plat (Figure 8), en concordance avec les derniers résultats sur l’anisotropie du fond diffus du cosmos.

Figure 8 : les âges de l’expansion d’un univers plat. (figure à venir) Univers plat: Ω=ΩΛ + ΩM =1 W.L. Freedman: Final results from the HST Key Project to measure the Hubble constant. 2001 (69)

Le travail le plus difficile a sans doute été de déterminer quels seraient les bons étalons afin de déterminer cette constante, grâce à laquelle il est possible d’exprimer avec certitude pratiquement tous les facteurs cosmologiques (Ω et Λ, l’âge de l’univers, la taille de l’univers observable : H0t0). Les supernovae de type Ia et les céphéides sont des points repères dans l’observation du passé, des étalons qui permettent de déterminer avec précision la distance séparant la Terre des objets les plus lointains du cosmos (~400Mpc soit plus de 1 milliard d’années-lumière). On peut espérer être capable(s) un jour de reconstituer la vie de l’univers ainsi que son devenir avec une certitude quasi irréprochable.