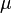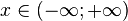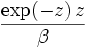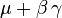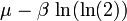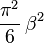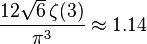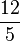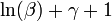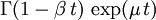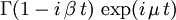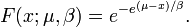Distribution de Gumbel - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Gumbel | |
|---|---|
| |
| |
| | |
| Paramètres |
 scale (real) scale (real) |
| Support |
|
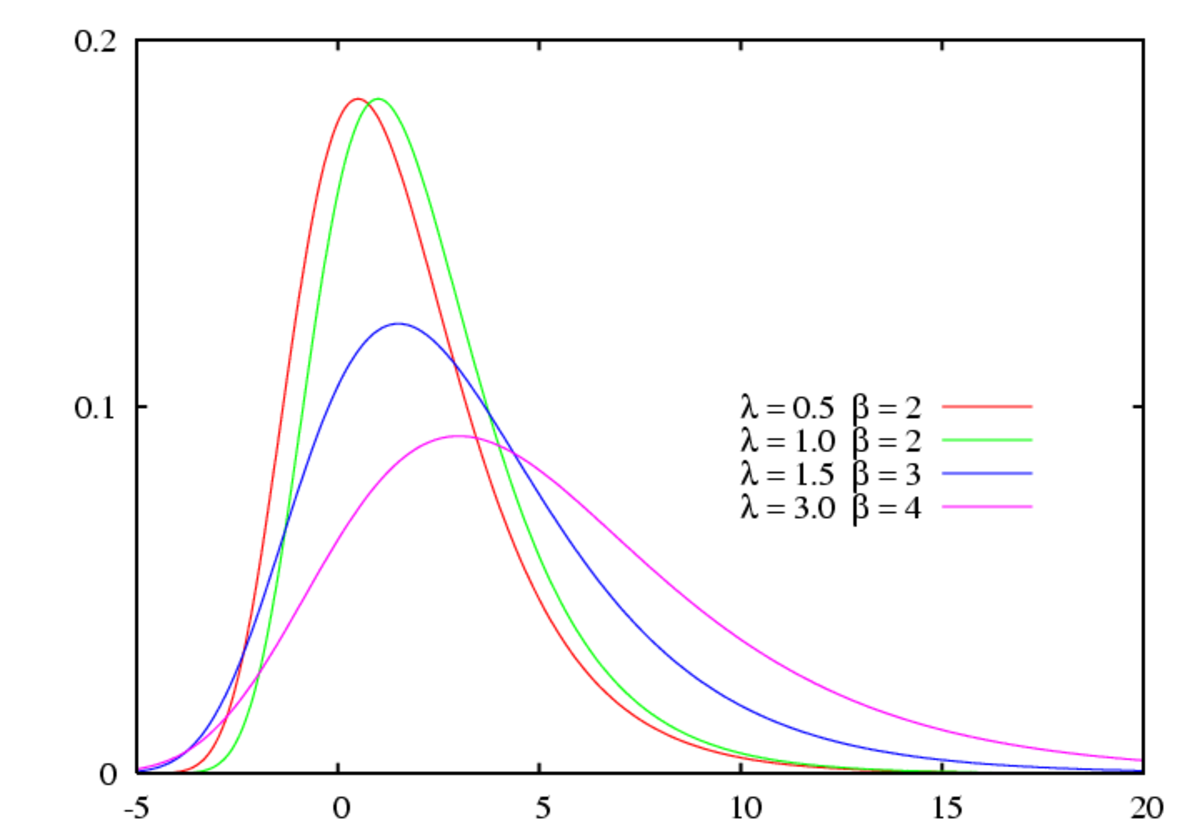
| Densité de probabilité (fonction de masse) |
avec ![z = \exp\left[-\frac{x-\mu}{\beta}\right]\!](https://static.techno-science.net/illustration/Definitions/autres/3/39335168375a14882ef3d924cefd58fd_76aea36e4744225c006ab88f5e6fa105.png)
|
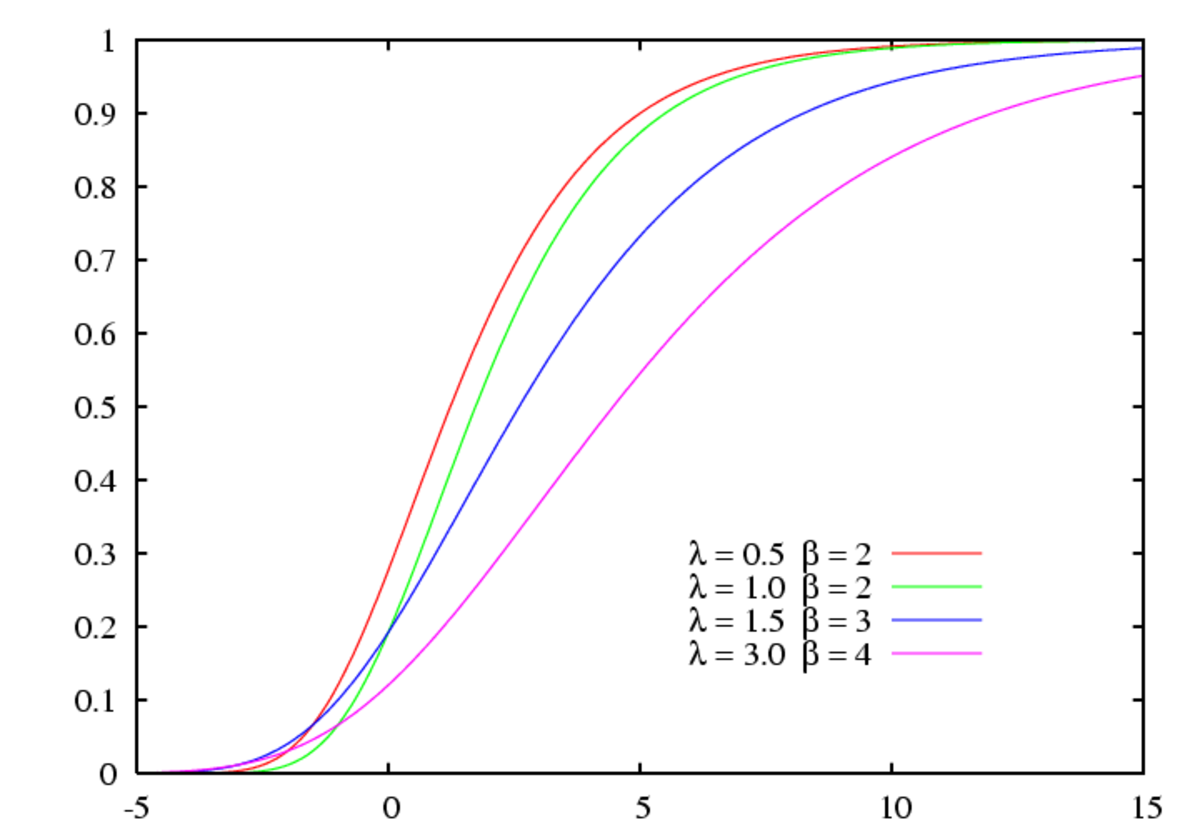
| Fonction de répartition | |
| Espérance |
|
| Médiane (centre) |
|
| Mode |
|
| Variance |
|
| Asymétrie (statistique) |
|
| Kurtosis (non-normalisé) |
|
| Entropie |
pour  |
| Fonction génératrice des moments |
|
| Fonction caractéristique |
|
| modifier | |
En théorie des probabilités, la distribution de Gumbel ou loi de Gumbel, nommée d'après Émil Julius Gumbel, est une distribution de probabilité continue. C'est une distribution particulièrement importante en théorie des valeurs extrêmes : la distribution de Gumbel est une bonne approximation de la loi du maximum d'un échantillon de variables aléatoires indépendantes et de même loi, dès que cette loi appartient, précisément, au domaine d'attraction de la loi de Gumbel. Parmi les lois appartenant au domaine d'attraction de la loi de Gumbel, on compte la loi exponentielle.
La distribution de Gumbel peut, par exemple, servir à prévoir le niveau des crues d'un fleuve, si on possède le relevé des débits sur dix ans. Elle peut aussi servir à prédire la probabilité d'un événement critique, comme un tremblement de terre.
Fonctions caractéristiques
La fonction de répartition de la loi de Gumbel est :
Pour μ = 0 et β = 1, on obtient la loi standard de Gumbel.
À voir
Notes
- Regular variation, Bingham, Goldie et Teugels.
Bibliographie
- (en) N. H. Bingham, C. M. Goldie et J. L. Teugels, Regular Variation, Cambridge University Press, coll. « Encyclopedia of Mathematics and its Applications » (no 27), Cambridge, juin 1989, 1re éd., 516 p.