Géométrie euclidienne - Définition

Vers d'autres géométries

Le concept de géométrie est maintenant appliqué à un vaste ensemble d'espaces. Si la remise en question du cinquième postulat est l'exemple historique qui donne un contenu à la notion de géométrie non euclidienne, une analyse plus précise montre l'existence de quantité d'autres cas non envisagés par Euclide respectant néanmoins le cinquième postulat.

Dans le cas des espaces vectoriels, le corps de nombres peut être modifié, la distance est parfois choisie de manière à posséder un nouveau groupe d'isométries, le nombre de dimensions peut devenir infini.

Il existe en outre de nombreux cas où l'espace n'est pas un espace vectoriel ; Klein formalise des géométries non orientables ; Georg Cantor découvre un ensemble triadique dont la dimension n'est pas entière et qui maintenant est classé dans la catégorie des géométries fractales. La topologie ouvre la porte à la construction de nombreux autres cas.

C'est la raison pour laquelle le terme de géométrie non euclidienne tombe petit à petit en désuétude durant le XX^e siècle. Il est maintenant entré dans l'usage de décrire une géométrie par les propriétés qu'elle possède et non pas par une, devenue très spécifique et qu'elle n'aurait pas, à savoir son caractère euclidien.

Les exemples suivants sont parmi les plus fréquemment utilisés.

Dimension infinie

Les espaces de fonctions à valeurs réelles disposent d'une structure d'espace vectoriel. Il est fécond de les étudier avec des outils géométriques. Il est possible d'y associer une distance issue d'un produit scalaire par exemple si les fonctions sont de carré intégrable. Ce produit scalaire est défini de la manière suivante :

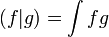
Dans un tel espace, le théorème de Pythagore se généralise et a permis à Joseph Fourier de résoudre l'équation de la chaleur.

Cette approche, consistant à utiliser les outils de la géométrie pour résoudre des problèmes d'analyse est maintenant dénommée analyse fonctionnelle. De multiples distances différentes sont définies sur ces espaces, engendrant alors des géométries distinctes. Suivant les propriétés plus ou moins fortes qu'elles possèdent, elles prennent pour nom espace de Hilbert, espace de Banach, espace préhilbertien ou espace vectoriel normé. L'espace de Hilbert est la généralisation la plus naturelle des géométries euclidiennes.

Espace hermitien

Les nombres réels souffrent d'une faiblesse, le corps qu'ils forment n'est pas algébriquement clos. Cela signifie qu'il existe des polynômes non constants qui n'y ont pas de racine. Cette faiblesse complique l'analyse des applications linéaires d'un espace vectoriel dans lui-même. L'article sur les valeurs propres explicite cette difficulté. Une solution souvent utilisée consiste à généraliser le corps de nombres et à passer aux complexes. Cette méthode est utilisée en physique, par exemple pour l'étude des systèmes oscillants. La généralisation d'un espace euclidien aux nombres imaginaires est dénommée espace hermitien.

Espace de Minkowski

Le cône de lumière en relativité restreinte.

La physique de la relativité restreinte propose un monde régi par des lois différentes de celle de la mécanique classique. Il n'y est pas possible de dépasser une vitesse critique, celle de la lumière. Cette limite engendre de nombreuses conséquences. Pour reprendre l'exemple d'Albert Einstein un voyageur dans un train en marche et se déplaçant dans le sens du train n'a plus, comme vitesse par rapport au sol, la somme exacte de la vitesse du train et de son déplacement, mais un tout petit peu moins.

La modélisation physique utilise un espace de dimension quatre contenant à la fois l'espace et le temps. Il est associé à une géométrie différente. Si l'on note x, y, z et ct les quatre coordonnées d'un point dans un repère orthogonal, en géométrie euclidienne le carré de la distance du point à l'origine est donnée par la formule : x² + y² + z² + (ct)², expression qui a le statut mathématique de forme quadratique. Dans le monde de la relativité restreinte, la formule : x² + y² + z² - (ct)², qui est aussi une forme quadratique, joue un rôle analogue. Ici, c désigne la célérité de la lumière et t une durée, la formule est bien homogène. Muni de cette forme, l'espace est dit de Minkowski.

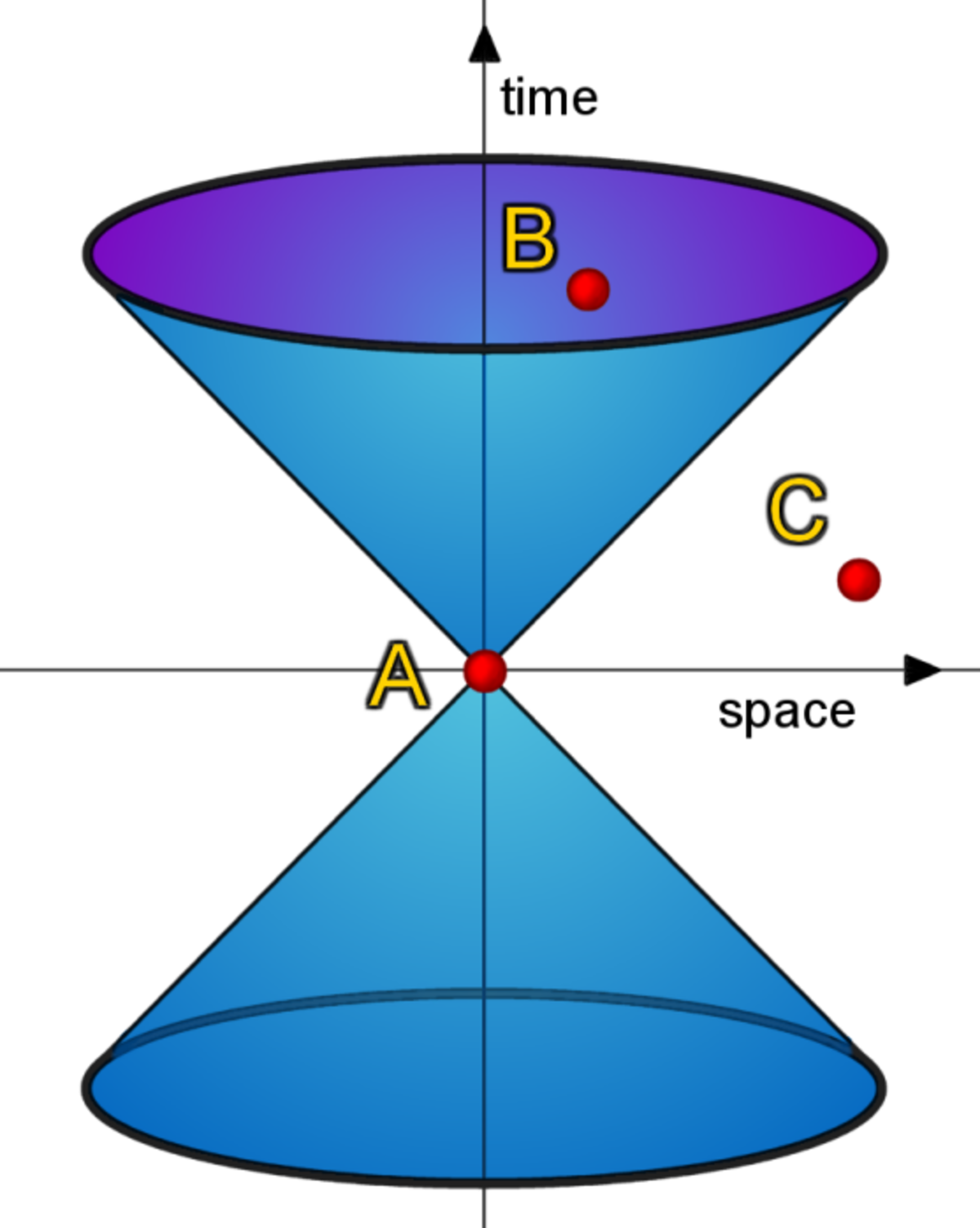
La modification d'un signe dans l'égalité définissant la forme quadratique (le "carré de la distance"), change la nature de la géométrie associée : cette quantité n'est plus nécessairement positive. Pour aller du centre noté A sur la figure de droite au point C, il est nécessaire de dépasser la vitesse de la lumière. Le carré de la distance entre A et C est strictement négatif, cette distance est purement imaginaire. En effet, si le carré de la distance est strictement négatif, la vitesse nécessaire pour atteindre le point C à partir du point A est supérieur à celle de la lumière. En conséquence et dans le cadre de la relativité restreinte, ce point ne peut pas être en interaction avec A.

L'ensemble des points à distance (spacio-temporelle) nulle de A forme un cône appelé cône de lumière de A. Ce cône est constitué des points qui supposent un déplacement à la vitesse de la lumière pour être joints à partir du point A (dans sa partie supérieure, future) ; et de l'ensemble des points joignant A à la vitesse de la lumière (dans sa partie inférieure, passée).
Il correspond à la limite physique des points de l'espace-temps en interaction possible avec A :

• L'intérieur supérieur du cône peut être vu comme l'ensemble des emplacements futurs possibles du point A, ou de l'ensemble des points qui seront causalement reliés avec A.
• L'intérieur inférieur comme l'ensemble des emplacements passés possibles de A, ou de l'ensemble des points causalement reliés à A.

Plus généralement, l'ensemble des points à égale distance (spacio-temporelle) de A est un hyperboloïde, alors que dans le cas euclidien l'ensemble des points à égale distance d'un centre, définit une sphère.

Variété

Sur une sphère, la somme des angles d'un triangle n'est pas égale à 180° : une sphère n'est pas un espace euclidien. Par contre, les lois de la géométrie euclidienne sont de bonnes approximations locales. Pour un petit triangle sur la surface de la Terre, la somme des angles est proche de 180°.

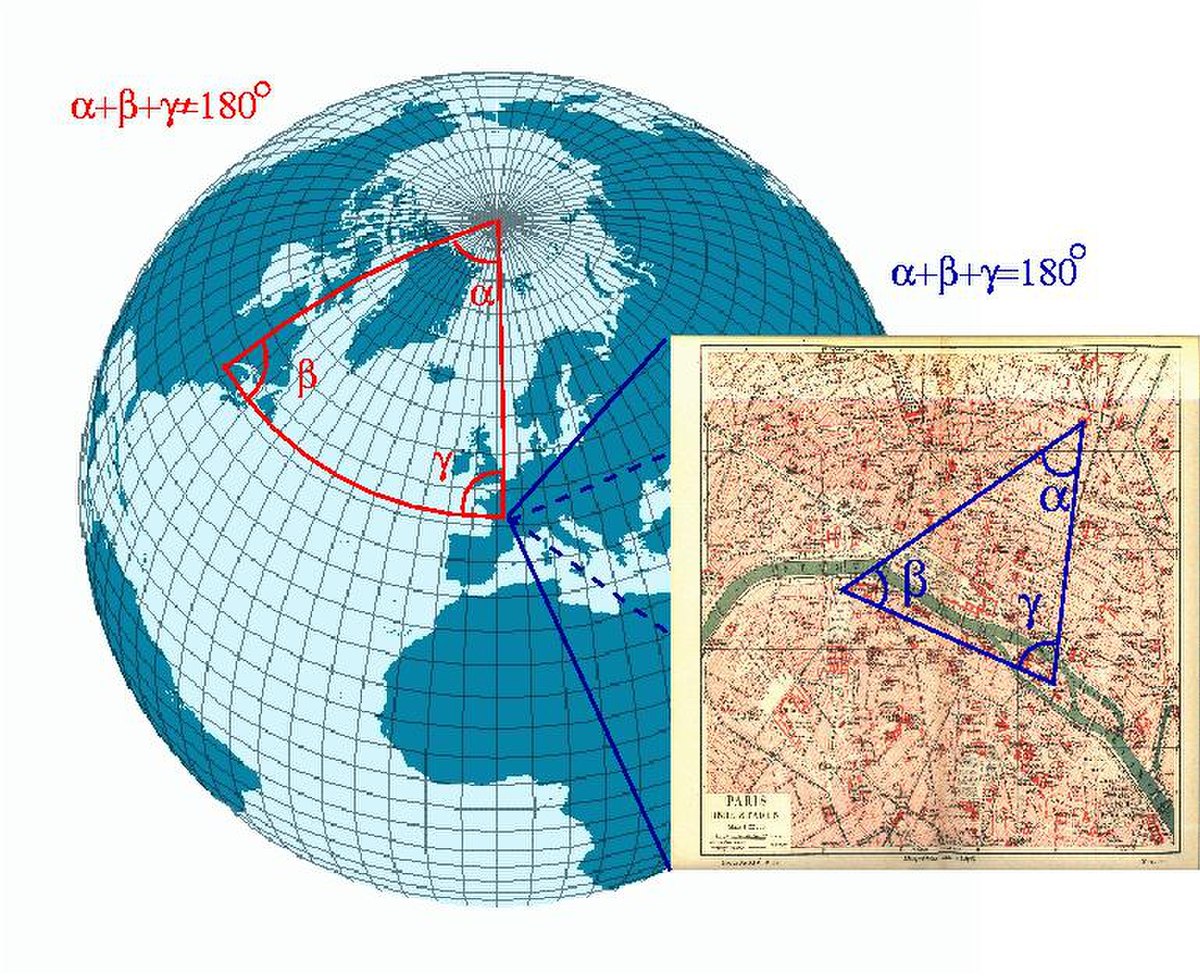
Toutes les géométries ne satisfont pas le cinquième postulat d'Euclide. La surface d'une sphère donne un exemple immédiatement accessible. Le plus court chemin entre deux points se situe toujours le long d'un grand cercle dont le centre est celui de la sphère. Cette courbe joue donc le rôle de droite pour la géométrie de la sphère. Voilà une géométrie cohérente, correspondant à un cas réel. Cependant le cinquième postulat n'est plus vérifié. Dans cet exemple, deux « droites » non confondues possèdent toujours deux points d'intersection.

L'abandon du cinquième postulat est fondamental. Il est en effet souhaitable de considérer la sphère, non pas comme un sous-ensemble d'un espace euclidien de dimension 3 mais comme une géométrie à part entière, disposant d'une distance et d'une relation d'orthogonalité. Sans outil de cette nature, l'étude d'un tel espace devient plus délicate.

La formalisation mathématique est dérivée de l'exemple illustré dans la figure. Si l'étude se résume à une zone suffisamment petite, alors il est possible d'utiliser une carte plane, c’est-à-dire une représentation euclidienne. En se rapprochant suffisamment du point d'étude, celle-ci donne une représentation d'une précision aussi grande que voulue. Ainsi, un plan de Paris ne sera jamais rigoureusement exact car sur une sphère la somme des angles d'un triangle est toujours supérieure à 180 degrés. Cependant, la dimension de Paris (relativement à celle de la Terre) est suffisamment petite pour que l'erreur soit négligeable.

Ce mode de définition de la géométrie des espaces courbes, par la donnée d'une famille de cartes locales, peut être généralisé. On obtient ainsi une description d'espaces courbes usuels (courbes et surfaces telles que la sphère), mais aussi, la possibilité de construire par la même méthode des espaces courbes abstraits portant le nom de variétés. La géométrie riemannienne est la branche des mathématiques qui étudie les espaces courbes sur lesquels existent des distances et des angles, et qui portent le nom de variétés riemanniennes. La recherche et l'étude des plus courts chemins, ou géodésiques, est une des préoccupations importantes de cette branche.

L’astrophysique à grande échelle ne peut pas se contenter de la géométrie riemannienne. En théorie de la relativité générale, les modèles utilisés ne sont plus basés sur la géométrie euclidienne, mais le sont plutôt sur l'espace de Minkowski. Le cadre d'étude est toujours un espace courbe (variété), mais on considère une forme quadratique qui n'est plus nécessairement positive ; la variété devient lorentzienne (ou, plus généralement, pseudo-riemannienne).
Ainsi, la gravitation se manifeste par la trajectoire incurvée suivie par une masse le long d'une géodésique non euclidienne.