Coordonnées homogènes - Définition
En mathématique, les coordonnées homogènes, introduites par August Ferdinand Möbius, rendent les calculs possibles dans l'espace projectif comme les coordonnées cartésiennes le font dans l'espace euclidien. Les coordonnées homogènes sont largement utilisées en infographie et plus particulièrement pour la représentation de scènes en trois dimensions (3D) car elles sont adaptées à la géométrie projective et elles permettent de caractériser les transformations de l'espace. La notation sous forme matricielle est plus particulièrement employée dans les bibliothèques de programmation graphique 3D telles que OpenGL et Direct3D.
Premières notations et interprétations
Les coordonnées homogènes d'un point de l'espace projectif de dimension n sont écrites habituellement comme (x:y:z: ... :w), un vecteur de longueur n+1, autre que (0:0:0: ... :0). Deux ensembles de coordonnées qui sont proportionnels dénotent le même point d'espace projectif : pour tout scalaire non-nul c pris du corps de base K, (cx:cy:cz: ... :cw) est équivalent à (x,y,z,w). Ainsi, ce système de coordonnées introduits des classes d'équivalences constituées de vecteurs colinéaires. Prenant l'exemple de l'espace projectif de dimension trois, les coordonnées homogènes seront (x:y:z:w).
L'espace projectif construit permet de caractériser le plan à l'infini. Celui-ci est en règle générale défini par l'ensemble des points ou vecteurs ayant pour dernière coordonnée w = 0. Hors de ce plan nous pouvons utiliser (x/w, y/w, z/w) comme un système cartésien ordinaire; donc l'espace affine complémentaire au plan à l'infini est coordonné dans une forme familière, avec une base correspondant à (1:0:0:1), (0:1:0:1), (0:0:1:1).
Si nous essayons de faire l'intersection de deux plans définis par les équations x = w et x = 2w alors nous dériverons d'abord w = 0 et ensuite x = 0. Cela nous indiquera que l'intersection est contenue dans le plan à l'infini et consiste de tous les points avec des coordonnées (0:y:z:0). C'est une ligne et en fait la ligne joignant (0:1:0:0) et (0:0:1:0). La ligne est donnée par l'équation :(0:y:z:0) = μ(1 − λ)(0:1:0:0) + μλ(0:0:1:0) où µ est un facteur scalaire. Ce dernier peut être ajusté pour normaliser les coordonnés (0:y:z:0), donc éliminant l'un des deux degrés de liberté. Le résultat est un ensemble de points avec un seul degré de liberté comme cela est attendu d'une ligne.
Combinaisons linéaires de vecteurs décrits avec les coordonnées homogènes
Prenons une paire de vecteurs A et B dans un espace en trois dimensions projectif, donc les coordonnées homogènes sont
On souhaite trouver leur combinaison linéaire
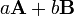
- les deux vecteurs dépendent d'un 3-espace affine,
- les deux vecteurs sont infinis,
- un vecteur est affine et l'autre est infini.
Les coordonnées X, Y, et Z peuvent être considérés comme numérateurs, W comme un dénominateur. Pour ajouter des coordonnées homogènes il est nécessaire que le dénominateur soit commun. Autrement il est nécessaire de redimensioner les coordonnées jusqu'à ce que tous les dénominateurs soient communs.
Les deux points sont affines
Si chacun des deux vecteurs sont dans un 3-espace affine, alors
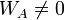
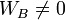
Les deux vecteurs sont infinis
Si chacun des deux vecteurs est infini, alors WA = 0 et WB = 0. Leur combinaison linéaire est
- a(XA:YA:ZA:WA) + b(XB:YB:ZB:WB) = (aXA:aYA:aZA:0) + (bXB:bYB:bZB:0)
-
-
-
-
- = (aXA + bXB:aYA + bYB:aZA + bZB:0).
-
-
-
-
Nous obtenons un autre vecteur infini.
Un vecteur est affine et l'autre est infini
Le premier vecteur est dans un 3-espace affine, donc
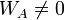
- a(XA:YA:ZA:WA) + b(XB:YB:ZB:0)
- = a(0:0:0:0) + b(XB:YB:ZB:0),
- = (bXB:bYB:bZB:0),
Nous obtenons un vecteur infini colinéaire au vecteur infini de la combinaison linéaire donc équivalent à ce dernier. Ceci signifie qu'un vecteur à l'infini est " dominant ", en théorie des ensembles on dit que c'est un élément absorbant.
Notation matricielle
Un point M de l'espace peut être, si W=1, désigné par ses coordonnées homogènes en 3D sous la forme (X:Y:Z:1). Les coordonnées homogènes sont alors utilisées pour appliquer des transformations à un point 3D telles que les changements de repères, les rotations, les translations, les homothéties, les projections ainsi que les compositions de ces différents opérateurs de base. Ces transformations sont alors représentées sous la forme d'une matrice (mathématiques) de taille
Les translations
La matrice traduisant une translation dans l'espace écrite sous la forme d'un vecteur (tx:ty:tz) est sous la forme :
![\left[ \begin{matrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{matrix} \right]](https://static.techno-science.net/illustration/Definitions/autres/1/135f3a923a48924b3d8cc773b6119bd1_d1d9d43aea1bc3b700778490c722a472.png)
En effet, si l'on calcule les coordonnées du point M' de coordonnées (sX':sY':sZ':s) qui est l'image de M par la translation citée, nous appliquons la multiplication matricielle suivante :
![\left[ \begin{matrix} sX' \\ sY' \\ sZ'\\ s \end{matrix} \right] = \left[ \begin{matrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} X \\ Y \\ Z \\ 1 \end{matrix} \right]](https://static.techno-science.net/illustration/Definitions/autres/3/3c999426c1a272d8976eb077e9733cf7_186c782392d0cdb48ba462ee6a9a0849.png)
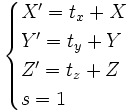
Calculer un vecteur
Soient deux points, appelés origine O et extrémité E, de coordonnées homogènes (Xo:Yo:Zo:Wo) et (Xe:Ye:Ze:We), les W n'étant pas nuls puisque les points sont affines, alors le 'vrai vecteur' du plan affine de dimension 3 qui permet de se translater du point O au point E a pour coordonnées :
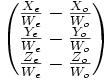
Vérification : L'équation matricielle de la translation appliquée au point O correspondant à ce vecteur s'écrit
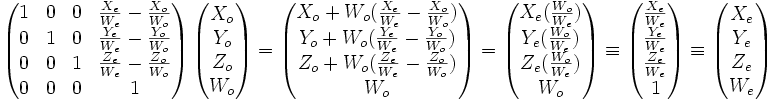
La translation appliquée nous permet de retrouver le point d'extrémité E du vecteur.
Relation de Chasles
La relation de Chasles est d'une lecture immédiate sous cette forme :
-
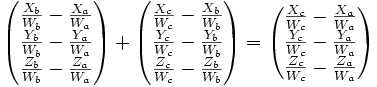
De même, avec cette notation, si l'on considère quatre points A, B, C et D, la commutativité de l'addition des vecteurs et le théorème du croisement des équipollences sont évidents.
Les rotations
Une représentation dans l'espace peut être aussi notée sous forme matricielle. L'opérateur sera de la forme :
![\left[ \begin{matrix} R_{3\times3} & 0_{3\times1} \\ 0_{1\times3} & 1 \end{matrix} \right]](https://static.techno-science.net/illustration/Definitions/autres/b/ba58b0695f8f33431dca37c2ad31a9c3_083cc701f97820520d75b19fb4e432e8.png)
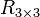
Rotation d'angle α autour de
![\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & \cos( \alpha ) & -\sin (\alpha) & 0 \\ 0 & \sin( \alpha ) & \cos ( \alpha) & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right]](https://static.techno-science.net/illustration/Definitions/autres/4/401c54a8c062c3e1cf1e59d2f63f9384_522d6f546b66f61674f0111f0a206871.png)
Rotation d'angle β autour de
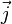
![\left[ \begin{matrix} \cos(\beta) & 0 & \sin(\beta) & 0 \\ 0 & 1 & 0 & 0 \\ -\sin( \beta ) & 0 &\cos ( \beta) & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right]](https://static.techno-science.net/illustration/Definitions/autres/1/19c925845400463cac9f01bf29ccedb1_723ae36791c7fd057d3642af5a904897.png)
Rotation d'angle γ autour de
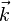
![\left[ \begin{matrix} \cos(\gamma) & - \sin(\gamma) & 0 & 0 \\ \sin(\gamma) & \cos(\gamma) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right]](https://static.techno-science.net/illustration/Definitions/autres/6/62d7a0b633c5de81602a962ac8d1c6f7_0af97c33af7a3143609029335d8d8362.png)
Les homothéties
Une homothétie sera représentée par la matrice :
![\left[ \begin{matrix} h_x & 0 & 0 & 0\\ 0 & h_y & 0 & 0\\ 0 & 0 & h_z & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right]](https://static.techno-science.net/illustration/Definitions/autres/5/575a53cb49b333afb491e5adca2c55d3_bd2f0f2326bc46732b53caed14452bb5.png)
Si les facteurs d'échelle hx,hy et hz sont égaux alors il s'agit d'un homothétie au sens strict du terme. Cette formalisation permet d'appliquer différents facteur d'échelle suivant différentes directions de l'espace (dilatation anisotropique).
Les projections
Il existe diverses formulations des projections, suivant le type de projection considéré. Nous ne verrons ici que les formulations les plus courantes rencontrées en infographie 3D.
La projection perspective
Nous prendrons ici le cas d'une projection sur un plan
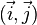
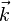
![\left[ \begin{matrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 1/f & 0 \end{matrix} \right]](https://static.techno-science.net/illustration/Definitions/autres/1/10e46da4240bcc4d0d055992319bcaa7_5cf92228c68084071c17239de011a03a.png)
En effet, si l'on calcule les coordonnées du point projeté M' de coordonnées (sX':sY':sZ':s1) qui est l'image de M par la projection citée, nous obtenons :
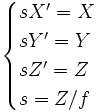
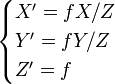
Comme la troisième coordonnée est toujours connue (égale à f), il est possible de déterminer directement les coordonnées 2D sur le plan lui-même. Nous avons alors le passage de coordonnées homogènes 3D à des coordonnées homogènes 2D. Si l'on prend M' de coordonnées sur le plan (sx',sy',s) image de M de coordonnées (X,Y,Z,1) alors la relation liant les deux points sera écrite sous la forme :
![\left[ \begin{matrix} sx' \\ sy'\\ s \\ \end{matrix} \right] = \left[ \begin{matrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{matrix} \right] \left[ \begin{matrix} X \\ Y\\ Z\\ 1\\ \end{matrix} \right]](https://static.techno-science.net/illustration/Definitions/autres/1/1d6767fe65ef0efc77c5575bc5ebb3e7_993c624ce4a56c779a347c40e321cd72.png)
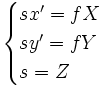
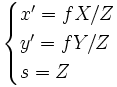
Nous retrouvons alors les mêmes valeurs que précédemment ( x' = X' et y' = Y'). Nous avons donc une formulation qui donne directement les coordonnées du point projeté sur le plan considéré.
Projection orthographique
Dans ce cas, les points sont projetés suivant une direction déterminée sur un plan situé à une distance f de l'origine suivant la direction
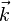
![\left[ \begin{matrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & f\\ 0 & 0 & 0 & 1 \end{matrix} \right]](https://static.techno-science.net/illustration/Definitions/autres/0/014cb6a6afd0c44adf420bc4da125bcb_e24b9b741c375c96270eec051ff259c8.png)
Application au changement de repère isométrique
Les coordonnées homogènes prennent tout leur intérêt dans ce cas précis. En effet, cette notation permet de traduire les changements de repère. Si le nouveau repère est translaté par rapport à l'ancien d'un vecteur
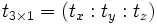
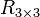
La transformation inverse sera donnée comme suit, où
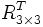
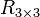
| Articles de mathématiques en rapport avec l'algèbre linéaire |
| Espace vectoriel | Base | Dimension | Matrice | Application linéaire | Déterminant | Trace | Rang | Théorème des facteurs invariants | Réduction d'endomorphisme | Réduction de Jordan | Décomposition de Dunford | Valeur propre | Polynôme caractéristique | Forme linéaire | Espace dual | Orthogonalité | Produit scalaire | Produit vectoriel | Polynôme d'endomorphisme | Polynôme minimal | Tenseur | Pseudovecteur | Covecteur | Algèbre multilinéaire |
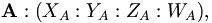
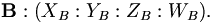
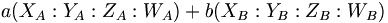
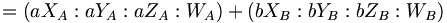
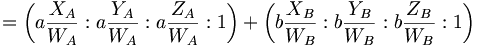
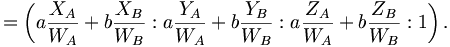
![\left[ \begin{matrix} sX' \\ sY' \\ sZ'\\ s \end{matrix} \right] = \left[ \begin{matrix} & & & \\ & R_{3\times3} & & t_{3\times1} \\ & & & \\ 0 & 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} X \\ Y \\ Z \\ 1 \end{matrix} \right]](https://static.techno-science.net/illustration/Definitions/autres/5/5a5f14758bc142811b114be42a0b9ae3_ab5083b4d0f6fed9a2e189353bddbcac.png)
![\left[ \begin{matrix} sX \\ sY \\ sZ\\ s \end{matrix} \right] = \left[ \begin{matrix} & & & \\ & R_{3\times3}^T & & -R_{3\times3}^Tt_{3\times1} \\ & & & \\ 0 & 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} X' \\ Y' \\ Z' \\ 1 \end{matrix} \right]](https://static.techno-science.net/illustration/Definitions/autres/f/f68efde8d89dafece019a5103ae325f1_20964124744d44c55d77c3e6f3d2d41e.png)

















































