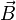Polarisation (optique) - Définition

Introduction

La polarisation est une propriété des ondes vectorielles telles que la lumière. Le fait que ces ondes soient caractérisées par des vecteurs les différencie des autres types d'ondes comme les ondes sonores, et implique ce phénomène de polarisation.

Théorie

Explication du phénomène

La manifestation la plus simple de polarisation est celle d'une onde plane, qui est une bonne approximation de la plupart des ondes lumineuses. Comme toute onde électromagnétique qui se propage, elle est constituée d'un champ électrique et d'un champ magnétique tous deux perpendiculaires à la direction de propagation :

Onde lumineuse avec champ magnétique et champ électrique à angle droit l'un de l'autre (dans le cas d'une polarisation rectiligne).

On décide, par convention, d'ignorer le champ magnétique par la suite, car il peut être déterminé à partir du champ électrique. On considère donc uniquement le champ électrique perpendiculaire à la direction de propagation.

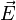
Conformément à la représentation ci-dessous, la figure décrite par le champ électrique peut être alors :

• un segment de droite, cas de la polarisation rectiligne ;
• une ellipse, cas de la polarisation elliptique ;
• un cercle, cas de la polarisation circulaire.

Les trois figures en mouvement ci-dessous illustrent, pour chacun des trois cas, l'évolution temporelle du champ électrique dans un plan d'onde fixé. Ces différentes formes définissent l'état de polarisation de l'onde : on dit que l'onde est polarisée rectilignement, elliptiquement ou circulairement.

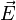
Rectiligne	Elliptique	Circulaire

De plus, cette onde se propage dans l'espace, selon une direction précise, que l'on choisit verticale, perpendiculaire au plan d'onde horizontal, dans les figures ci-dessous (en trois dimensions) : ces courbes sont une représentation spatiale, instantanée, au temps t₀ fixé, des positions de la pointe de flèche du champ électrique dans tous les plans d'onde superposés verticalement le long de la propagation ; ces courbes sont construites en reportant à la distance verticale d le vecteur champ qui existait dans le plan d'onde du bas à un instant passé t = t₀ − d / v (v est la vitesse de propagation ; on tient compte ainsi de l'effet de la propagation) :

• La courbe de gauche représente la polarisation rectiligne ; c'est une sinusoïde tracée dans le plan vertical, passant par la diagonale du carré bleu, en bas.
• La courbe de droite représente la polarisation circulaire ; c'est une hélice qui s'enroule sur un cylindre vertical, dont la base est le cercle dessiné en perspective dans le carré du bas.
• La courbe du milieu représente la polarisation elliptique ; c'est une courbe ressemblant à une hélice, tracée sur un cylindre vertical, aplati, dont la base est l'ellipse dessinée dans le carré du bas.

Rectiligne	Elliptique	Circulaire

On peut se figurer la propagation en faisant glisser verticalement ces représentations spatiales instantanées : un instant Δt plus tard, ces courbes doivent être remontées de la distance Δd = vΔt.

La symétrie des fonctions de l'espace et du temps, dans les équations de propagation, fait que les mêmes courbes peuvent aussi représenter mathématiquement les variations temporelles du champ électrique , dans un plan d'onde fixé, telles que nous les avons vues en mouvement dans la représentation animée ci-dessus (Il suffit alors de graduer en temps l'axe vertical).

Ce phénomène s'explique grâce à l'équation de propagation de l'onde lumineuse. En décomposant le champ électrique en ses deux composantes orthogonales (en vert et rouge sur les schémas précédents), on s'aperçoit qu'elles ont toutes deux une évolution sinusoïdale. Lorsque les deux composantes oscillent en même temps, on obtient une polarisation rectiligne. Si elles présentent un déphasage (c'est-à-dire que l'une est en retard par rapport à l'autre), alors on obtient une polarisation elliptique.

Dans le cas particulier où ce déphasage vaut 90° et que les deux composantes ont même amplitude, la polarisation est circulaire. On distingue alors les cas de polarisation circulaire gauche et circulaire droite selon le sens de l'enroulement autour du cylindre.

Remarque : Cette décomposition en deux composantes orthogonales est arbitraire. Il est aussi possible, par exemple, de décomposer en deux polarisations circulaires tournant en sens contraires.

La lumière incohérente

L'explication ci-dessus n'est valable strictement que pour une onde monochromatique, et plus particulièrement une lumière cohérente. Dans les autres cas, les effets sont un peu différents.

Par exemple, dans la lumière d'une ampoule à filament, on observe que la lumière est polarisée aléatoirement : elle ne correspond à aucun des trois cas précédents. Cela s'explique par le fait que cette lumière est composée de trains d'ondes, courtes impulsions lumineuses ayant chacune une amplitude, une fréquence, et une polarisation aléatoires. Ainsi, ce que nous observons est une moyenne de tous ces trains d'ondes qui nous apparaît non polarisée.

Toutefois, la lumière incohérente peut aussi présenter, en partie, une polarisation elliptique, circulaire, ou rectiligne. Pour déterminer alors quelle est la polarisation d'une lumière, on utilise des polariseurs et des lames à retard.

Représentation des états de polarisation

Il peut être nécessaire de représenter mathématiquement un état de polarisation de lumière, par exemple, afin de suivre son évolution à travers un système optique. On peut notamment utiliser :

• le formalisme de Jones, particulièrement adapté à la représentation d'états complètement polarisés ;
• les paramètres de Stokes, associés aux matrices de Mueller, qui permettent de décrire également la lumière partiellement polarisée.

Aspect corpusculaire

Toutes les explications ci-dessus sont données dans le cadre de l'optique ondulatoire. Cependant, la polarisation peut également être expliquée en utilisant l'aspect corpusculaire de la lumière.

La lumière est composée de photons possédant un spin de 1. La physique quantique nous enseigne donc que pour un photon, la projection sur un axe de son spin peut uniquement prendre les valeurs -1, 0 ou +1. Cependant, la valeur 0 est interdite par la théorie quantique des champs car la masse du photon est nulle. Les deux états propres correspondent donc soit à la valeur propre +1 (polarisation circulaire droite) ou à la valeur propre -1 (polarisation circulaire gauche). Conformément à la physique quantique, l'état de polarisation du photon est une combinaison linéaire de ces 2 états propres, ce qui permet de définir les polarisations rectilignes et elliptiques .