Valeur propre, vecteur propre et espace propre - Définition

Introduction

Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre associée est proche de -1/2. Dans ce cas particulier l'espace propre est l'espace entier.

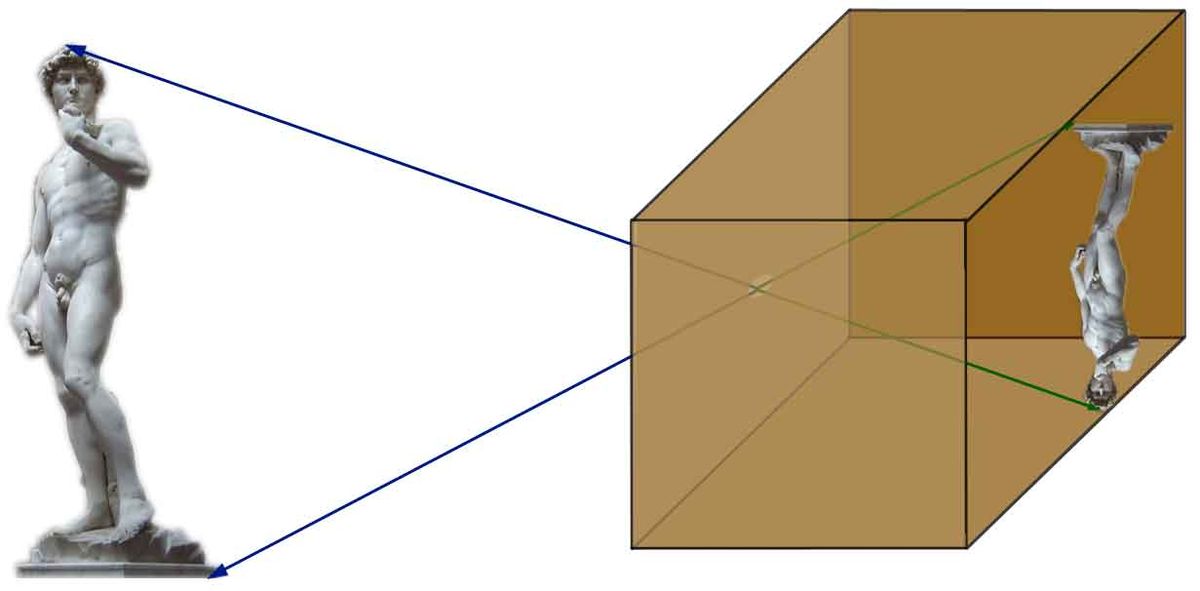
En mathématiques, le concept de vecteur propre est une notion algébrique s'appliquant à une application linéaire d'un espace dans lui-même. Il correspond à l'étude des axes privilégiés, selon lesquels l'application se comporte comme une dilatation, multipliant les vecteurs par une même constante. Ce rapport de dilatation est appelé valeur propre, les vecteurs auxquels il s'applique vecteurs propres, réunis en un espace propre. Le graphique de la figure 1 illustre ces notions.

La connaissance des vecteurs et valeurs propres offre une information clé sur l'application linéaire considérée. Il existe de plus de nombreux cas où cette connaissance caractérise totalement l'application linéaire.

Ce concept appartient à l'origine à une branche des mathématiques appelée algèbre linéaire. Son utilisation, cependant, dépasse maintenant de loin ce cadre. Il intervient aussi bien en mathématiques pures qu'appliquées. Il apparaît par exemple en géométrie dans l'étude des formes quadratiques, ou en analyse fonctionnelle. Il permet de résoudre des problèmes appliqués aussi variés que celui des mouvements d'une corde vibrante, le classement des pages web par Google, la détermination de la structure de l'espace-temps en théorie de la relativité générale, ou l'étude de l'équation de Schrödinger en mécanique quantique.

• Pour un article synthétique sur le sujet ne traitant que du contenu mathématique, voir : Valeur propre (synthèse)

Histoire

Genèse

René Descartes associe algèbre et géométrie et démarre l'algèbre linéaire.

S'il est habituel de prendre pour acte de naissance officiel de l'algèbre la publication du livre d'Al-Khuwārizmī , qu'il décrit lui même comme « un abrégé englobant les plus fines et les plus nobles opérations du calcul », le domaine linéaire doit attendre le XVI^e siècle pour dépasser le simple cadre de quelques équations.

L'association entre la géométrie et l'algèbre, à travers la notion de coordonnées, fut introduite en 1637 par René Descartes et Pierre de Fermat . Le contexte est donné pour l'apparition de premiers résultats d'algèbre linéaire comme le calcul d'un déterminant. Ces résultats serviront par la suite d'outil d'analyse des valeurs propres. Cependant, les mathématiques de cette époque ne disposent pas encore des notions indispensables de l'algèbre linéaire, comme une géométrie correspondant à notre espace vectoriel, où les éléments sont définis par leurs opérations.

Le début du XIX^e siècle voit l'apparition d'outils importants pour la théorie des valeurs propres. En 1799, Carl Friedrich Gauss démontre la clôture algébrique des nombres complexes. Des espaces vectoriels plus vastes sont étudiés. Gauss formalise le problème de la résolution d'un système d'équations linéaires avec la méthode du pivot en retrouvant une méthode décrite par un mathématicien chinois Liu Hui (III^e siècle après J.C) près de 1600 ans auparavant.

Des problématiques où les valeurs propres représentent la bonne approche sont étudiées. Joseph Fourier étudie une solution de l'équation de propagation à l'aide d'un outil que l'on appellera plus tard une base de vecteurs propres. Enfin en 1834, Hamilton utilise, un polynôme caractéristique pour trouver ce que l'on appelle maintenant les valeurs propres associées à l'endomorphisme d'une équation différentielle linéaire issue de la mécanique. Cependant, l'absence de formalisation suffisante de la notion d'espace vectoriel empêche l'apparition claire du concept.

Origine du mot

L'Allemand Hilbert donne la formulation anglosaxone : eigenvalue provenant de Eigenwert.

La formalisation algébrique d'un espace vectoriel apparait vers le milieu du siècle. Arthur Cayley initie l'étude des espaces vectoriels de dimension n et de leurs applications linéaires. Grassmann formalise le concept. Même si, en tant que mathématicien il est peu reconnu à cette époque, dès 1845, des idées analogues sont reprises par Cauchy et publiées sous une forme plus définitive neuf ans plus tard. Sylvester en collaboration avec Cayley utilise pour la première fois le terme de matrice en 1850. Il utilise la notion de valeur propre dans le cas des formes bilinéaires pour la résolution de problèmes sur le principe mécanique de l'inertie deux ans plus tard. La notion de matrice est finalement définie de manière générale et abstraite par Cayley en 1858.

Le Français Jordan donne la formulation française : valeur propre.

Jordan publie un livre définitif sur les endomorphismes en dimension finie et pour une large famille de nombres, dont les complexes et réels. Jordan analyse le rôle des vecteurs propres et de leur exact domaine d'application dans une théorie maintenant connue sous le nom de réduction d'endomorphisme. La finalité de son texte n'est pas l'algèbre linéaire mais la théorie des groupes et de leurs représentations. La théorie est ainsi présentée dans le contexte des corps finis. Il termine le chapitre des valeurs propres dans le cas de la dimension finie et des corps de nombres algébriquement clos. La terminologie française provient des travaux de Jordan.

Le début du XX^e siècle apporte un regard nouveau sur la géométrie. La résolution de l'équation intégrale amène certains mathématiciens à considérer une géométrie sur les ensembles de fonctions. Frigyes Riesz utilise des systèmes orthogonaux de fonctions. Erhard Schmidt soutient sa thèse sur un sujet analogue et sous la direction de David Hilbert . Les travaux de Hilbert apportent à la notion de valeur propre une nouvelle profondeur. Ils correspondent à la formalisation de la démarche intuitive qui avait amené Fourier à la résolution de l'équation de la chaleur. Les ensembles de fonctions deviennent un espace vectoriel dont la géométrie est calquée sur celle d'Euclide. L'équation intégrale devient l'analogue d'un système linéaire et l'application linéaire prend le nom d'opérateur différentiel. Une nouvelle branche des mathématiques est née : l'analyse fonctionnelle. Elle devient rapidement le cadre général de résolution d'une large famille de problèmes mathématiques, en particulier l'analyse, les équations différentielles ou les équations aux dérivées partielles. Les valeurs propres sont un des outils essentiels à la résolution de ces problèmes. Elles s'avèrent indispensables en physique pour des théories comme la mécanique quantique ou la relativité générale. Pendant une longue période les anglosaxons utilisent indifféremment les termes de proper value et eigenvalue, provenant respectivement de la traduction des textes de Jordan et de Hilbert. Le vocabulaire est maintenant fixé au bénéfice de la deuxième expression.

Valeur propre et XX^e siècle

À la fois dans le contexte de la dimension finie et pour le cas général, le XX^e siècle voit un développement massif de ces théories. Le cas de dimension finie subit deux évolutions : cette théorie est généralisée à d'autres ensembles de nombres que les réels ou les complexes. De plus, des mathématiciens comme Issai Schur, A. Krilov, W. E. Arnoldi ou N. Dunford développent quantités d'algorithmes pour permettre la détermination des valeurs propres. Le cas général est cependant le plus étudié. Il ouvre la voie à une branche importante tout au long de ce siècle, l'analyse fonctionnelle. La théorie des valeurs propres est alors généralisée à la théorie spectrale. Paul Dirac et John von Neumann étudient ce concept dans un cadre servant de modélisation à la physique. Israel Gelfand, Mark Naimark et Irving Segal appliquent ces concepts à des univers plus vastes, les C^* Algèbres. Sur la base de résultats de géométrie algébrique trouvés par Alexandre Grothendieck, Alain Connes développe un cas particulier de C^* Algèbres, les géométries non commutatives. La théorie spectrale reste encore un large champ d'investigations mathématiques, et nombre de problèmes sont toujours ouverts dans ce domaine.

Les valeurs propres, et dans son cas le plus général, la théorie spectrale ouvrent de nombreux champs d'applications à la fois théoriques et appliqués. En mathématique, cette approche permet par exemple la résolution d'équations différentielles, ou d'équations aux dérivées partielles. La physique utilise très largement la théorie spectrale : elle sert de cadre général à la mécanique quantique et permet par exemple l'étude de l'équation de Schrödinger. Les solutions de l'équation de Schrödinger indépendante du temps sont des vecteurs propres. Les théories physiques de la fin du XX^e siècle comme les supercordes utilisent largement les notions de spectre dans des cadres mathématiques avancés, par exemple les géométries non commutatives. Les sciences de l'ingénieur ne sont pas en reste, même si elles se cantonnent en général à une approche de dimension finie. Elles utilisent quantité d'algorithmes issus des calculs de valeurs propres et vecteurs propres. Cette approche permet de résoudre de multiples problèmes tirés par exemple de la mécanique statique ou dynamique, des systèmes électriques et même dans d'autres secteurs comme l'économie.