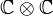Opération (mathématiques) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

Introduction

\begin{array}{rr}6 + 2 = &\!\! 8\\ 6\times2 = &\!\! 12\\ 6 - 2 = &\!\! 4\\ 6\div 2 = &\!\! 3\end{array}

En mathématiques, une opération est un processus visant à obtenir un résultat à partir d'un ou plusieurs objets appelés opérandes. L'écriture d'une opération implique en général l'utilisation d'un symbole spécifique appelé opérateur.

Exemples

En arithmétique, les quatre opérations élémentaires (addition, soustraction, multiplication et division) sont suivies par le carré, le cube et plus généralement les opérations puissance, la racine carrée, l'exponentiation, la factorielle… Plus généralement, beaucoup de fonctions peuvent être vues comme des opérations élémentaires, telles que la valeur absolue, la prise du logarithme ou de l'exponentielle, les fonctions trigonométriques…
En théorie des ensembles, les opérations ensemblistes usuelles sont la réunion, l'intersection, la différence symétrique et la complémentation. Elles ne doivent pas être confondues avec les opérations sur les ensembles telles que le produit cartésien, la somme disjointe ou l'exponentiation ensembliste.
En analyse, les fonctions peuvent subir des opérations de dérivation, intégration, convolution…
En logique, les opérations booléennes usuelles rassemblent une opération unaire (la négation) et cinq opérations binaires (la conjonction, la disjonction inclusive, la disjonction exclusive, l'implication et l'équivalence). Il est même possible de définir des opérations pour chacun des 2^2ⁿ connecteurs logiques n-aires.
En géométrie euclidienne, les opérations de symétrie, translation et rotation sont appelées des transformations.

Formalisme

Une opération peut correspondre à une loi de composition interne sur un ensemble, mais elle n'est pas nécessairement toujours définie (telle la division) pour tout choix d'éléments dans cet ensemble. Ainsi, selon les contextes, on parlera plutôt de loi de composition interne ou externe, de fonction de deux variables ou fonction de plusieurs variables, d'action voire de foncteur ou de bifoncteur.

v · d · m Notion de nombre
Ensembles usuels	$\mathbb{N}$ Entier naturel • $\mathbb{Z}$ Entier relatif • $\mathbb{D}$ Nombre décimal • $\mathbb{Q}$ Nombre rationnel • $\mathbb{R}$ Nombre réel • $\mathbb{C}$ Nombre complexe
Extensions	$\mathbb{H}$ Quaternion • $\mathbb{O}$ Octonion • $\mathbb{S}$ Sédénion • Nombre complexe fendu • Tessarine • $\mathbb{C}\otimes\mathbb{C}\,$ Nombre bicomplexe • $\mathbb{MC}_n$ Nombre multicomplexe • Biquaternion • Coquaternion • Octonion fendu • Nombre hypercomplexe • $\mathbb{Q}_p$ Nombre p-adique • Nombre hyperréel • Nombre superréel • Nombre dual • Droite réelle achevée • Nombre cardinal • Nombre ordinal • Nombre surréel et pseudo-réel
Propriétés particulières	Parité • Nombre premier • Nombre composé • Carré parfait • Nombre parfait • Nombre positif • Nombre négatif • Fraction dyadique • Nombre irrationnel • Nombre algébrique • Nombre transcendant • Nombre imaginaire pur • Nombre de Liouville • Nombre normal • Nombre univers • Nombre constructible • Nombre réel calculable • Nombre transfini • Infiniment petit • Infiniment grand
Exemples d’importance historique	π Pi • √2 Racine carrée de deux • φ Nombre d’or • 0 Zéro • $i$ Unité imaginaire • $e$ Constante de Neper • ℵ₀ Aleph-zéro • Table de constantes mathématiques
Notions connexes	Chiffre • Numération • Fraction • Opération • Calcul • Algèbre • Arithmétique • Suite d’entiers • ∞ Infini • Chiffre significatif