Pendule de Foucault - Définition

Un pendule de Foucault, du nom du physicien français Jean Bernard Léon Foucault, est une expérience conçue pour démontrer la rotation de la Terre par rapport à un référentiel galiléen ainsi que l'existence de la force de Coriolis dans un référentiel non galiléen défini naturellement, à l'endroit où il se trouve, par un observateur terrestre.
Historique : Les académiciens de Florence avaient observé vers 1660 le déplacement du plan d'oscillation du pendule. Mais ils ignoraient la cause de ce déplacement. Le physicien français, au contraire, qu'il devait avoir lieu comme conséquence du mouvement de la terre. C'est en voyant une tige cylindrique fixée dans le prolongement de l'arbre d'un tour, osciller dans un plan fixe pendant la rotation de l'arbrequ'il conçut la possibilité de prouver la rotation de la terre au moyen du pendule.[1]
La première démonstration date de 1851, le pendule étant accroché à la voûte du Panthéon de Paris. L'intérêt du pendule imaginé et réalisé par Foucault, est qu'il met en évidence la rotation de la Terre par une expérience locale aisément reproductible et que l'on peut également déterminer en quelques heures, par mesure de la déviation au sol du plan d'oscillation, la latitude du lieu de l'expérience sans aucune observation astronomique extérieure.
Si l'on considère le plan déterminé par :
- le point de fixation du pendule (la voûte du Panthéon par exemple),
- sa position au repos, donc la verticale du lieu où il est suspendu,
- le point d'où il est lâché sans vitesse initiale (sans vitesse relative locale),
l'expérience met en évidence :
- que le plan d'oscillation du pendule est en rotation autour de l'axe de la verticale du lieu,
- que ce plan d'oscillation tourne dans le sens horaire dans l'hémisphère nord et dans le sens inverse dans l'hémisphère sud.
- que le plan d'oscillation effectue un tour complet en 24 heures aux pôles (ou plus exactement en un jour sidéral), mais qu'ailleurs la période est plus longue et doit être divisée par le sinus de la latitude. A une latitude de 30°, la période est donc de 2 jours et à 45° de latitude de 1,4 jour. A l'équateur le pendule y oscille dans un plan fixe.
Cette expérience historique, répétée par la suite en de nombreux endroits, a permi de vérifier le bien-fondé des lois de Newton.
En 1851, les lachers du pendule avaient un certain cérémonial : le pendule était tendu par une corde qui faisait un aller-retour autour de la boule. On attendait la fin des oscillations du cable, puis on brûlait un des deux brins de la corde de sorte que le pendule soit libéré avec une vitesse nulle.
Aujourd'hui on trouve généralement un mécanisme magnétique qui permet d'entretenir le mouvement car en raison du frottement de l'air celui du Panthéon n'oscille que durant 6 heures.
L'expérience du pendule du Panthéon n'était pas suffisamment convaincante pour beaucoup de contemporains ce qui a poussé Foucault à inventer l'année suivante le gyroscope dont l'axe reste parallèle à une direction fixe par rapport aux astres et cela quelle que soit la latitude.
Mise en équation
Pour simplifier, nous supposerons l'amplitude des oscillations suffisamment faibles pour admettre que la masse oscillante du pendule se déplace horizontalement. Notons Oxy ce plan horizontal, avec O position de la masse au repos, Ox axe horizontal dirigé vers l'est (et donc tangent au parallèle), et Oy dirigé vers le nord (et donc tangent au méridien). Le troisième axe Oz sera vertical, dirigé vers le haut.
Cas du pendule simple
Sans tenir compte de la rotation de la Terre par rapport à un référentiel galiléen, les équations du mouvement sont celles du pendule simple, à savoir :
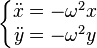
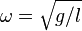
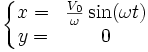
Cas du pendule de Foucault
Avec la rotation de la Terre par rapport à un référentiel galiléen, il faut tenir compte de la force de Coriolis dont l'accélération s'écrit
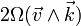


Si on se trouve à la latitude θ, alors le vecteur
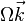
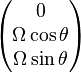


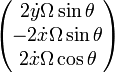
Les équations du mouvement dans le plan Oxy deviennent :
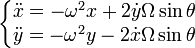
En utilisant la notation complexe z = x + iy, le système à résoudre s'écrit :
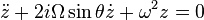
Proposons une solution classique de la forme z(t) = ert, on en déduit que le complexe r doit vérifier l'équation du second degré : r2 + 2iΩsin(θ)r + ω2 = 0 qui s'écrit aussi :
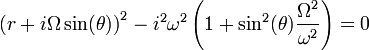
En notant
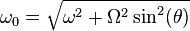
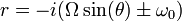
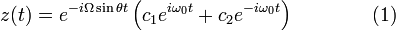
où c1 et c2 sont deux constantes, éventuellement complexes, qu'on peut déterminer par deux conditions initiales comme par exemple, la position du pendule et sa vitesse à la date t = 0 qui conduisent aux deux équations :
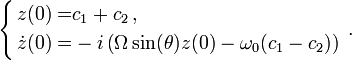
En remplaçant les expressions trouvées pour les deux constantes dans l'équation (1), on peut alors écrire une équation plus aisément interprétable :
![z(t) =e^{-i \Omega \sin{\theta} t} \left[z_0\left(\cos(\omega_0 t) +i \frac{\Omega \sin(\theta)}{\omega_0}\sin(\omega_0 t) \right) + \frac{\dot{z}_0}{\omega_0} \sin(\omega_0 t)\right] \qquad\qquad(2)](https://static.techno-science.net/illustration/Definitions/autres/7/722aa14a9af4716c07d245795de2044a_7e24dacffb3c041f006234c24206dd8d.png)
Ainsi, si
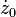
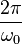
Si
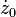
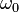
Examinons alors deux manières de lancer le pendule :

- Supposons que le pendule soit propulsé depuis la position d'équilibre (z(0) = 0 vers l'est à la vitesse
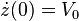
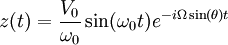
- Le pendule repasse exactement par sa position d'équilibre à chaque oscillation comme l'indique l'animation ci-dessus. L'animation est fictive et correspond à une rotation très rapide de la Terre et dans l'hémisphère sud.
- Mais on ne voit pas comment un tel mouvement peut être initié de manière simple.
- Supposons maintenant, comme le fit Foucault, que le pendule soit écarté de sa position d'équilibre par une corde tendue (par exemple vers l'est : z0 mètres) et qu'on la brûle afin de libérer le pendule avec une vitesse initiale nulle (
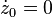
![z(t)= z_0 e^{-i\Omega\sin(\theta)t} \left[ \cos(\omega_0t) + i \frac{\Omega\sin(\theta)}{\omega_0} \sin(\omega_0 t) \right]\qquad\qquad(3)](https://static.techno-science.net/illustration/Definitions/autres/5/56f6e85e95f67fd82dede175f333c5dd_fa18d9f7c38045aa89c3895b9d5c25f5.png)
- et il suffit de tracer la courbe paramétrée par la partie réelle (longitude est) et la partie imaginaire (latitude nord) pour obtenir le tracé A beaucoup plus réaliste (cliquer sur la figure pour lire le programme de tracé en langage Gnuplot correspondant) même si la vitesse de rotation de la Terre est encore fictive et de l'ordre d'une rotation en 110 secondes au lieu d'une rotation par 24 heures.
Si on met une caméra dans le plan d'oscillation du pendule, on obtient l'animation B où le référentiel terrestre tourne. On peut remarquer que le pendule n'oscille pas rigoureusement dans le plan mais de part et d'autre du plan selon l'ellipse décrite plus haut. La longueur du fil étant fixe, on calcule pour chaque projection au sol x(t),y(t) la hauteur correspondante h(t) du pendule par rapport au sol.
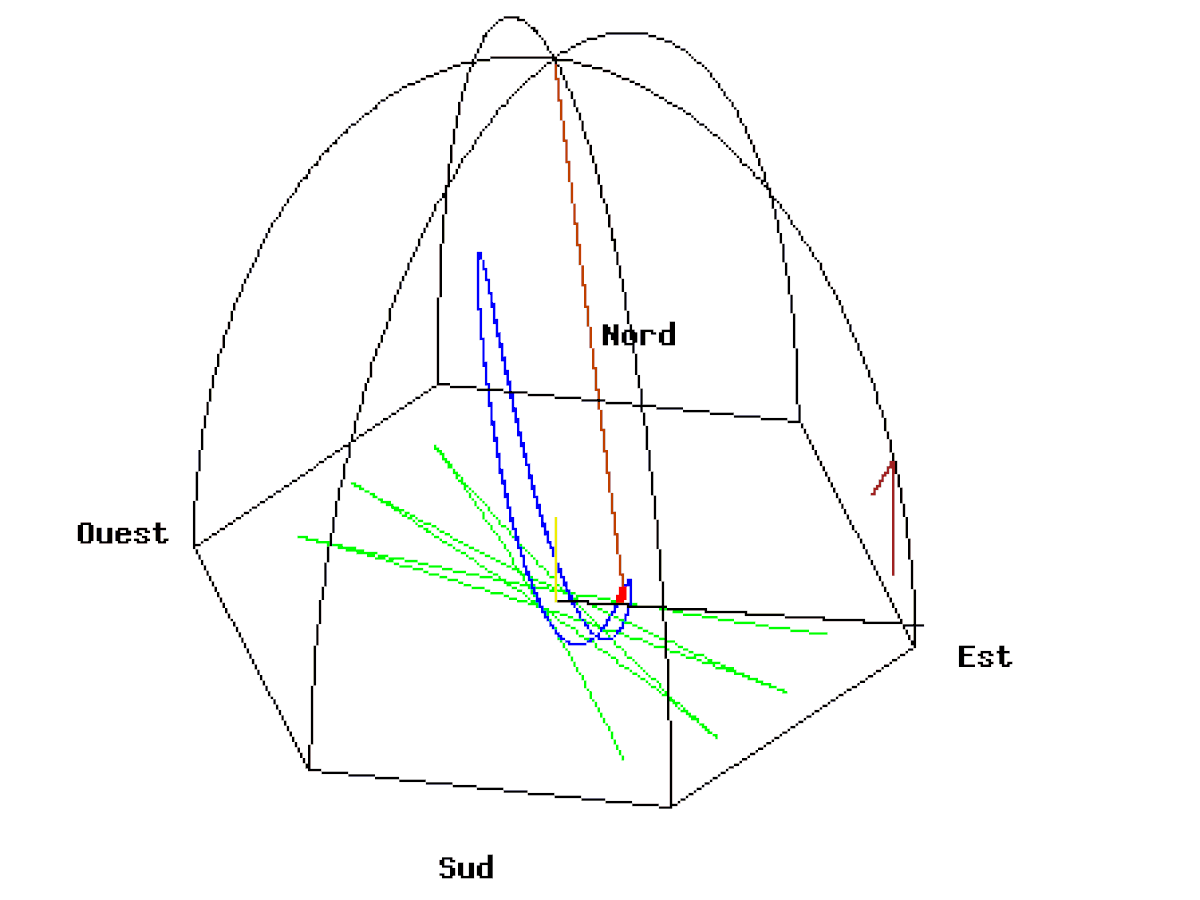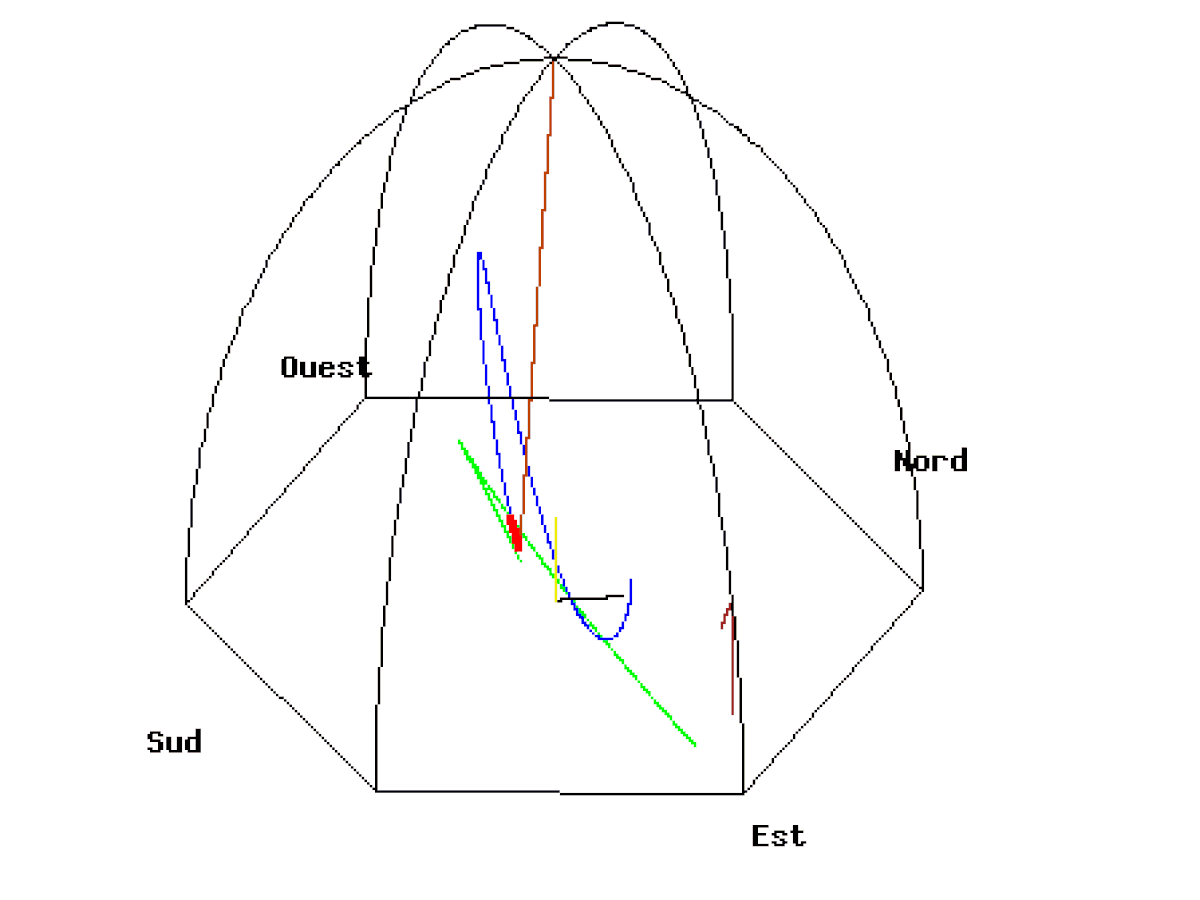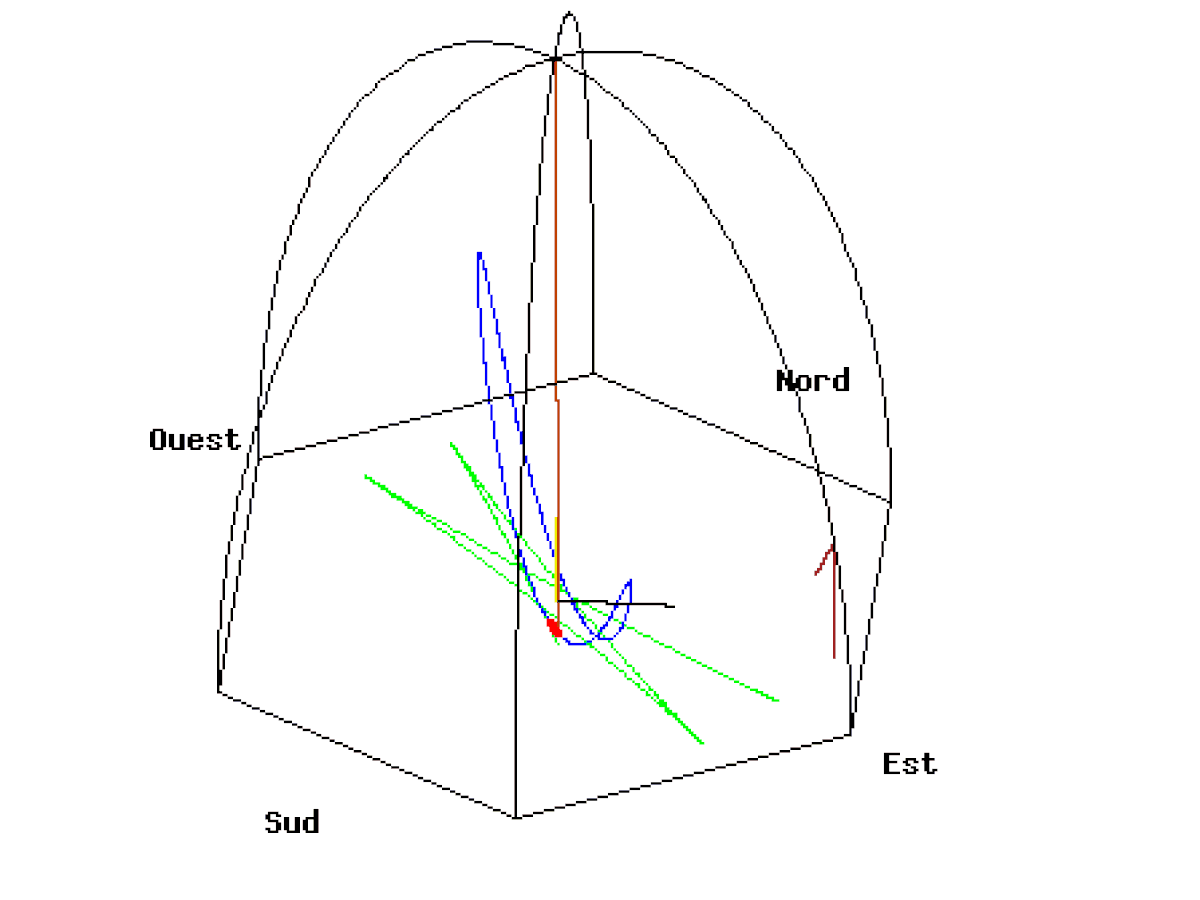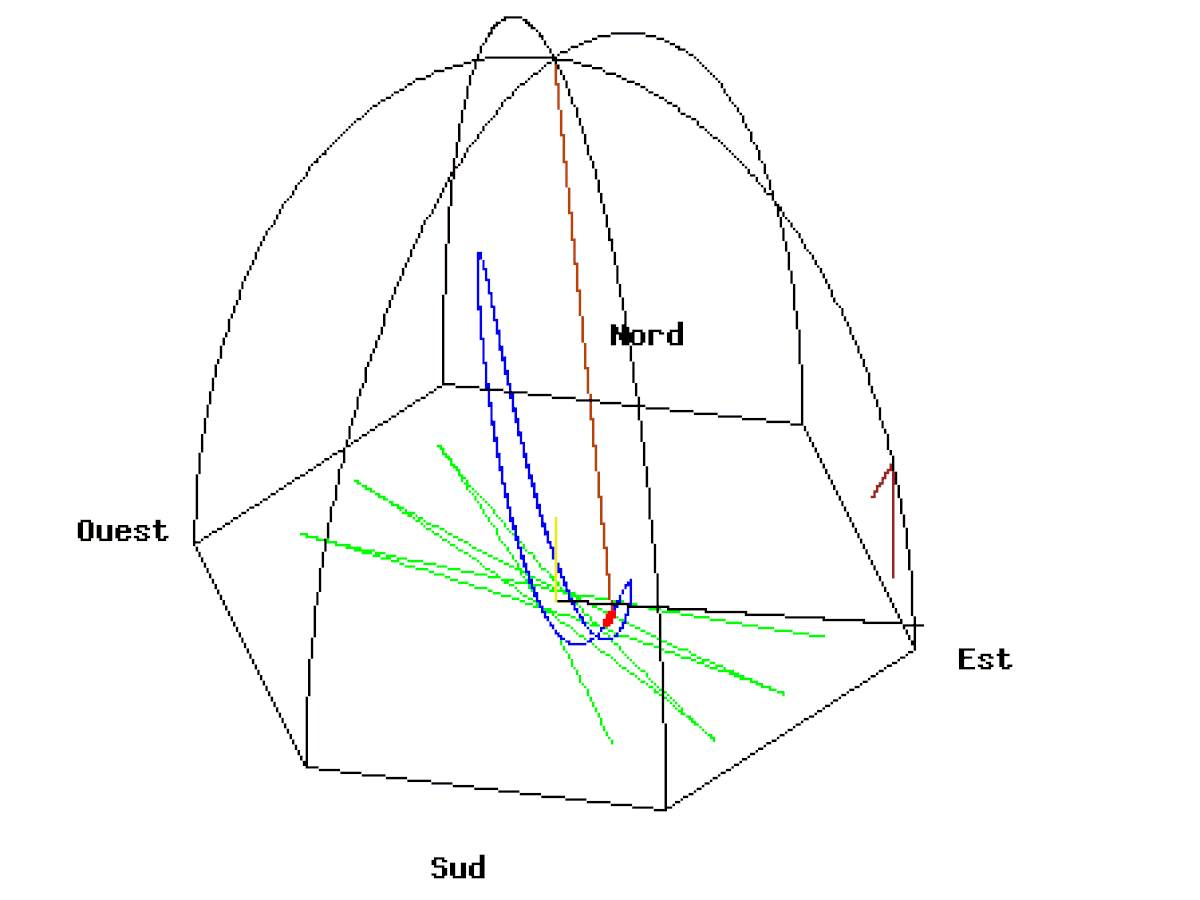
Il est également possible de voir le même pendule depuis le soleil, c’est-à-dire depuis une caméra fixe par rapport aux étoiles.
Le pendule de Foucault du Panthéon à Paris oscille sur notre vraie planète Terre avec une pulsation propre ω0 extrêmement proche celle du pendule simple ω (les 8 premiers chiffres sont identiques) puisque Ω est très petit devant ω. La période d'oscillation,
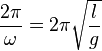
Le rapport du petit côté de l'ellipse sur le grand côté a pour expression
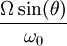
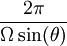
A la latitude nord de 48°52' du Panthéon à Paris, le plan tourne donc de
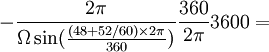
La Terre ne tournant pas uniquement sur elle-même, mais également autour du Soleil et d'autres astres l'influençant, la rotation du référentiel terrestre n'est pas de 24 heures par jour, mais de 23 heures 56 minutes par jour sidéral.
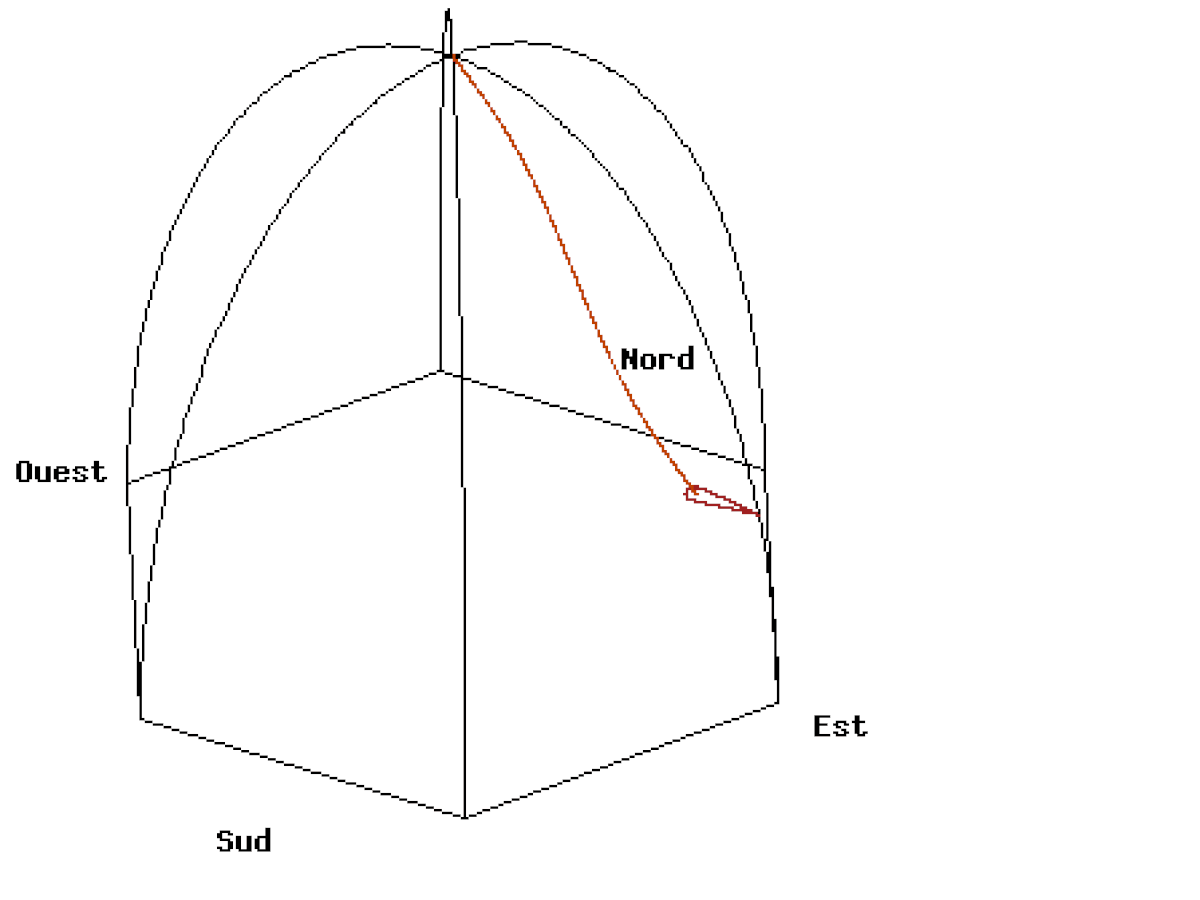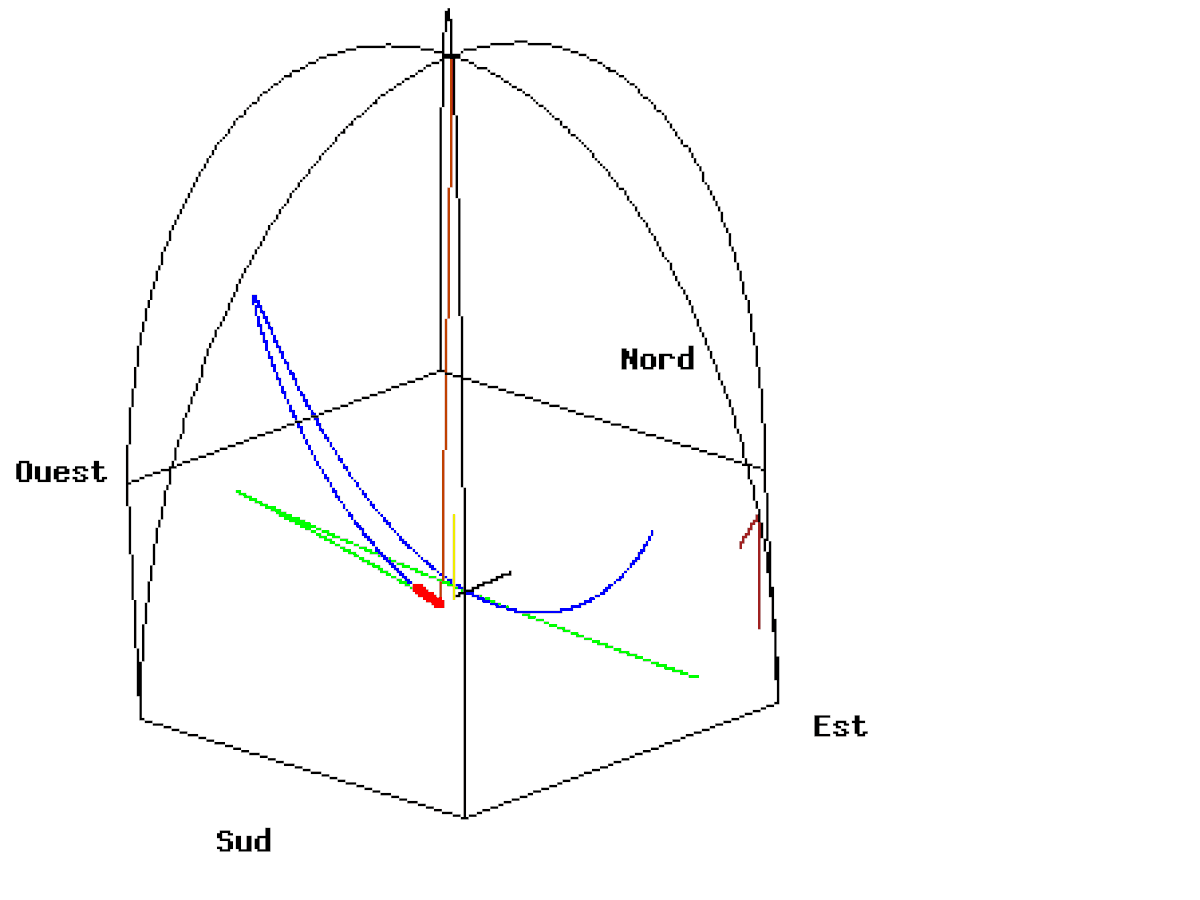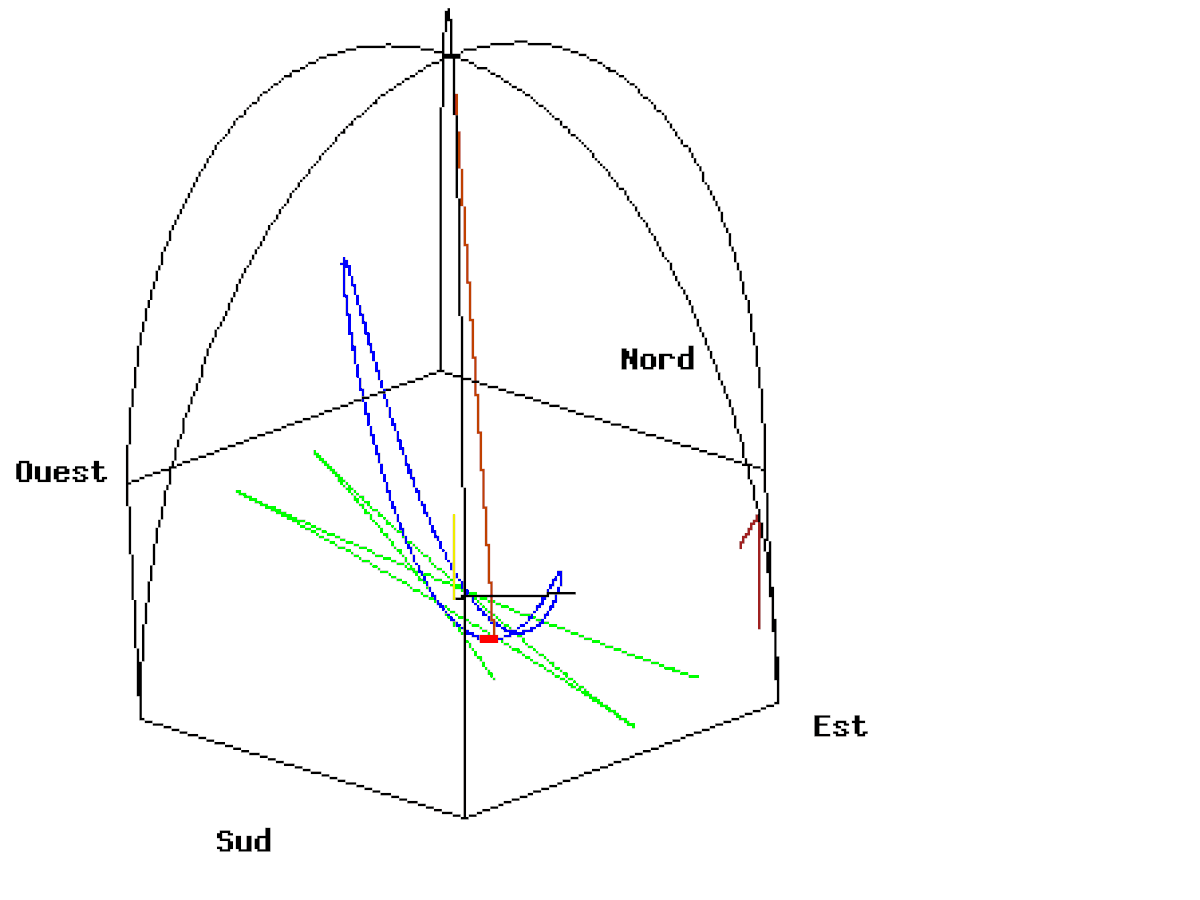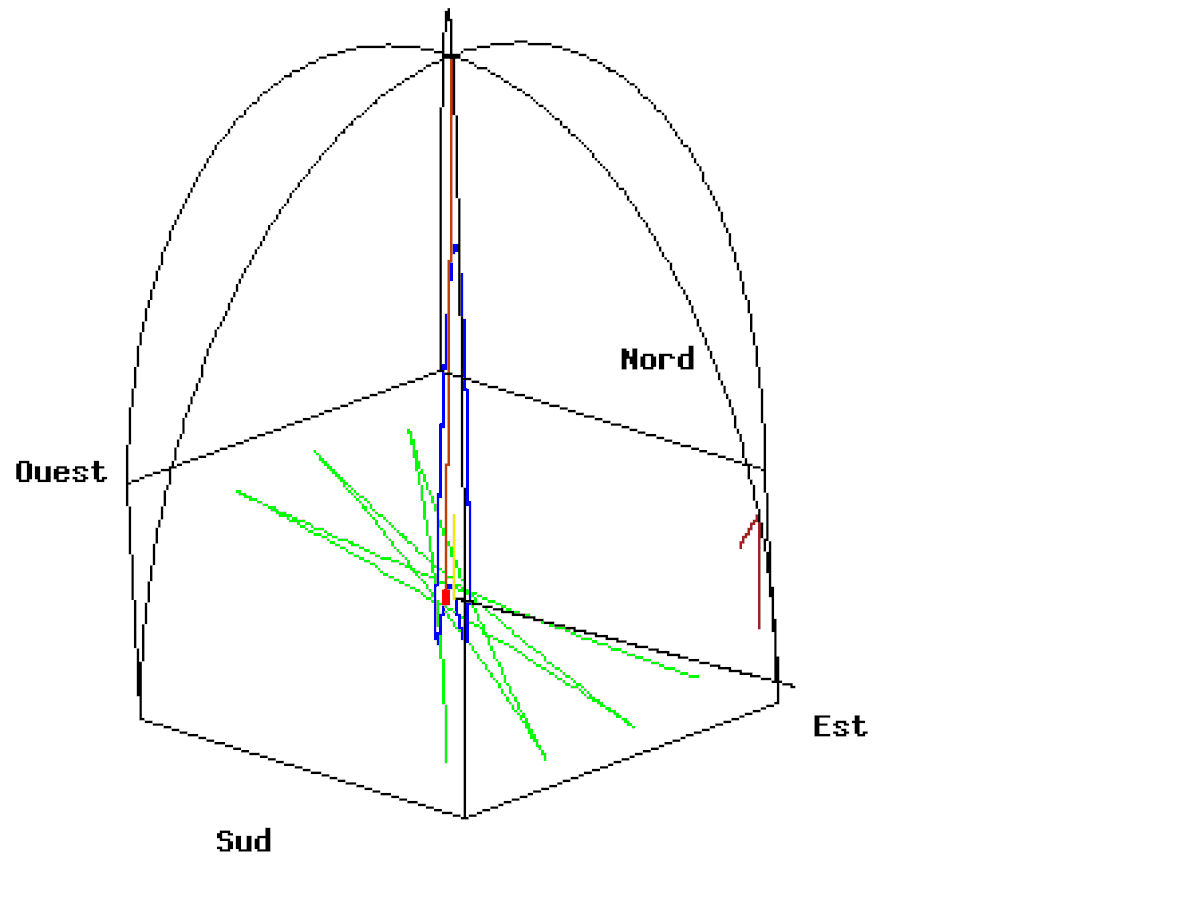
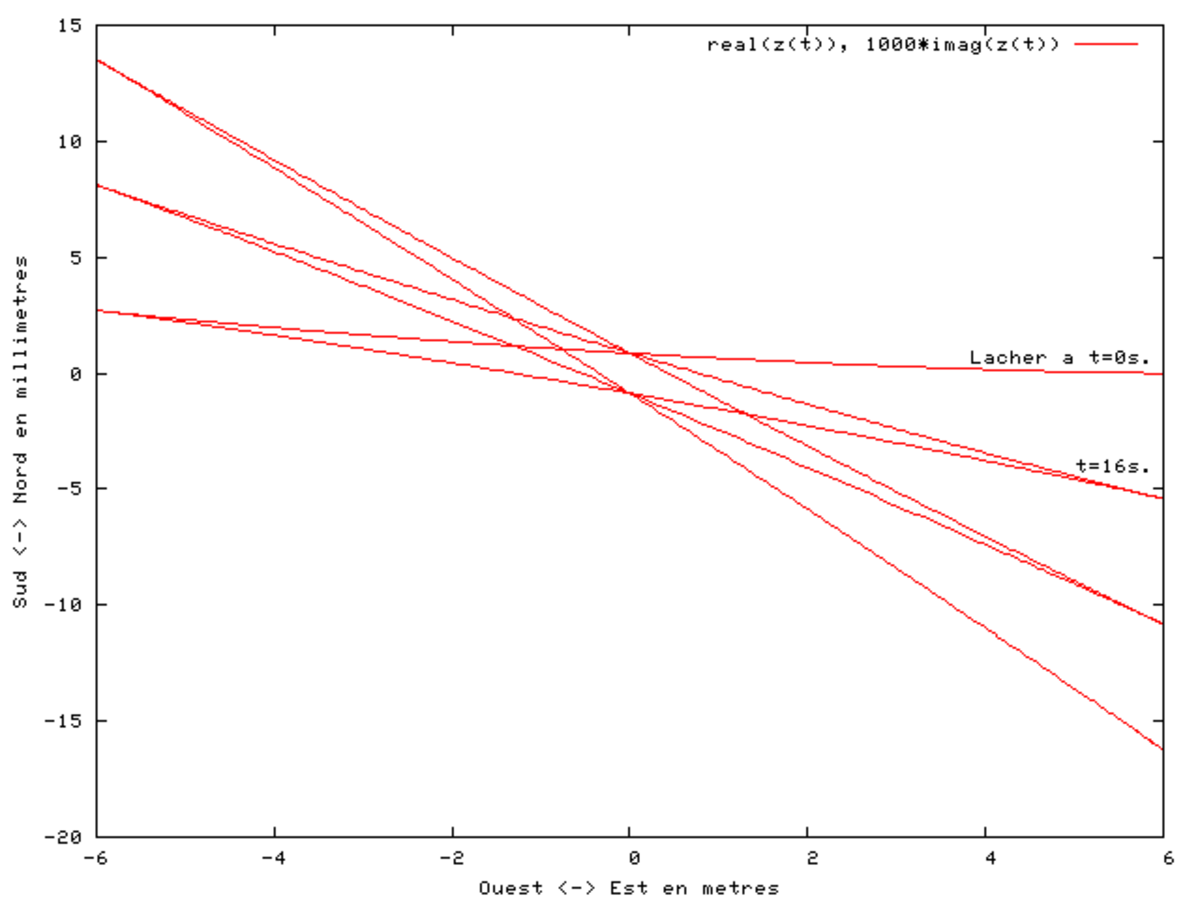
Nous avons ainsi représenté sur la figure ci-après les 3 premières oscillations après un lacher à vitesse nulle à une distance de 6 mètres à l'est du centre de la coupole du Panthéon. Etant donnée la faible déviation vers le nord par rapport au déplacement est-ouest du pendule durant ces trois premières oscillations, l'échelle de l'ordonnée (sud-nord) est multipliée par 1000 ce qui correspond à un déplacement en millimètre. La force de Coriolis, perpendiculaire au déplacement et proportionnelle à la vitesse, fait dévier le pendule de son plan d'oscillation initial vers le nord ; elle est maximale lorsque que la vitesse est maximale c’est-à-dire lorsque le pendule passe près du point d'équilibre, qu'il dépasse à 0,86 mm au nord (
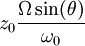
Le pendule revisité : quel système de référence ?
Le pendule de Foucault pose la question de la nature du repère qui sert de référence. En effet, tout mouvement est relatif. Si la Terre est en rotation, elle l'est par rapport à quelque chose. On ne peut pas parler d'un mouvement sans définir un cadre de référence. Ce cadre est un référentiel galiléen, mais comment ce référentiel est-il défini ? Plaçons le pendule Foucault au pôle. La Terre tourne par rapport à un repère galiléen selon l'axe terrestre avec la pulsation Ω. Le pendule tourne par rapport à la Terre avec une pulsation qui vaut au pôle − Ω, selon la verticale du lieu qui est également l'axe terrestre. Le pendule oscille donc dans un plan fixe par rapport à un repère galiléen.
Dans une première approximation, le plan du pendule est fixe par rapport au Soleil. Mais, si Foucault avait réussi à construire un pendule capable d'osciller suffisamment longtemps, disons pendant un mois, il se serait aperçu que le plan d'oscillation dérivait également par rapport à la position du Soleil. Notre étoile ne fait donc pas partie du système de référence en question.
Peut-être faut-il alors considérer les étoiles proches du Soleil ? Mais là aussi, si l'expérience pouvait durer suffisamment longtemps, elle montrerait que le plan des oscillations se déplace nettement par rapport aux étoiles après quelques années. Quel objet choisir dans ce cas ? Le centre galactique, la galaxie d'Andromède, le Groupe Local, le superamas local ? Chacun de ces objets donnerait l'illusion d'être fixe par rapport au plan des oscillations, mais finirait, après un temps de plus en plus long, par révéler une dérive.
Si l'expérience pouvait être menée suffisamment longtemps en considérant comme référence les objets les plus lointains de l'univers, les galaxies ou quasars situés à des milliards d'années-lumière, on pourrait constater encore une infime dérive du plan d'oscillation.
Finalement, l'ultime recours serait de considérer comme référence le rayonnement de fond de l'univers . Avec ce système de référence, et si l'expérience de Foucault était réalisable, le plan des oscillations serait enfin fixe et il n'y aurait plus de dérive. Ce n'est donc qu'en fonction de l'Univers dans son ensemble, que nous pouvons définir un référentiel galiléen par rapport auquel le plan des oscillations est fixe.
Le pendule de Foucault se moque donc de la présence du Soleil ou de la Galaxie. Son mouvement lui est directement dicté par l'Univers entier. Cette expérience met en évidence une sorte de lien mystérieux entre chaque point et l'Univers tout entier et Ernst Mach s'est posé la question de savoir quelle serait la Mécanique dans un Univers vide (voir Principe de Mach). Jusqu'à nouvel ordre, la nature de ce lien reste inconnue.
Effets parasites
La mise en évidence de la rotation terrestre par le pendule de Foucault est une expérience très délicate. Le plan d'oscillation du pendule tourne de quelques degrés par heure (maximum, 15° au Pôle). Plusieurs phénomènes risquent de masquer ce que l'on veut mettre en évidence :
- l'amortissement du pendule par le frottement dans l'air. Il est proportionnel à la section du pendule, son poids est proportionnel au volume : on choisira un objet dense et lourd.Il faut une sphéricité parfaite, un cylindre est parfois plus approprié pour de petites amplitudes ; ne surtout jamais utiliser une lentille de franc-comtoise.
- l'asymétrie du pendule. Celui-ci doit être parfaitement symétrique pour ne pas partir dans un sens ou dans l'autre. Il ne doit pas non plus pivoter sur lui-même : l'effet Magnus le dévierait de son plan d'oscillation.Néanmoins bien sûr il tourne légèrement sur lui-même, à raison de sa précession ! Il faut aussi veiller au point d'attache.
- Il doit être lancé sans composante perpendiculaire au plan d'oscillation. Comme il s'agit d'un pendule sphérique, on doit effectuer la correction d'erreur systématique : Victor Puiseux a montré que si le pendule effectuait une ellipse, celle-ci entraînait un effet de précession proportionnelle à son aire et inversement proportionnelle au carré de la longueur du pendule.
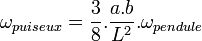
- l'astuce de l'anneau de Fernand Charron est peu connue (cf Bulletin de la SAF de novembre 1931) mais pourtant très efficace : on entretient le mouvement du pendule par un electroaimant très pointu, et le cylindre est lui-même muni d'une pointe qui vient quasiment en contact de celle de l'électroaimant : celui-ci est banalement alimenté par du 9V continu haché de la façon suivante : l'anneau de Charron (C) est placé à quelques décimètres du point d'oscillation O ( pour une longueur de 1,70 m environ): Quand le fil de suspension métallique touche l'anneau très bien centré, le courant passe : il y a force électromagnétique attractive : donc retard vers la montée, mais avance sur la descente, puis rien, puis symétriquement pour l'autre côté. L'astuce est que la self entraîne un retard dans le courant et donc il y a bien gain d'énergie au total. L'amplitude des oscillations (2 degrés environ) est imposée par le bilan énergétique : l'énergie perdue pendant une oscillation, qui croit avec l'amplitude est exactement compensée par l'énergie fournie par l'électroaimant. Certes la période du pendule est composée de deux mouvements : l'un autour de O et l'autre autour de (C)( de rayon très petit, 0,5 mm environ) : on peut le vérifier par la mesure de T (en effectuant évidemment toutes les corrections qui s'imposent (en particulier fil d'acier maintenu en O par un mandrin cylindrique). L'originalité du système n'est pas qu'il entretienne le pendule, MAIS que LE FROTTEMENT SOLIDE du fil sur l'anneau (C) pendant une partie du mouvement, loin de perturber la précession, est au contraire un très subtil moyen pour supprimer l'influence des conditions de lancement de départ qui sont si critiques. Celui du Palais de la Découverte marchait sur ce principe.
- Rappelons enfin que la thèse de Heike Kamerlingh Onnes portait sur l'expérience de Foucault et nos collègues hollandais ont bien de la chance d'avoir tous les calculs faits, dans toutes les situations possibles.
-- A améliorer/vérifier...
Divers

- Le pendule que Foucault a installé au Panthéon en 1851 mesurait 67 mètres et portait une masse de 28 kilogrammes. Une fois lancé, ce pendule oscille pendant 6h. La période (aller-retour) étant de 16,5 s, le pendule dévie de 11° par heure. Depuis 1995, ce pendule est à nouveau au Panthéon.
- Du 7 au 19 mars 2005 : dans le cadre de 2005 : Année Mondiale de la Physique, un pendule de Foucault de 25 mètres et d'une masse de 42 kilogrammes a été installé dans la collégiale Sainte-Waudru à Mons.
- Du 26 au 28 mai 2005 : en la cathédrale d'Auch, le pendule installé faisait 25 m de long pour une masse de 20 kg.
- En 2005, un pendule de Foucault a été installé à Bruxelles, au fond de l'avenue de Beaulieu.
- Du 1er février au 31 octobre 2006, un pendule de Foucault est installé à Padoue, au palazzo della Ragione.
- On peut voir un pendule de Foucault au Deutsches Museum de Munich.
- Un pendule de Foucault est installé au Musée des Arts et Métiers de Paris.



















































