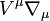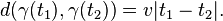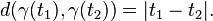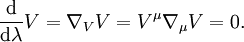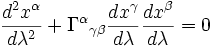Géodésique - Définition

En géométrie, une géodésique désigne le chemin le plus court, ou l'un des chemins s'il en existe plusieurs, entre deux points d'un espace une fois qu'on s'est donné un moyen de mesurer les distances, c’est-à-dire-une métrique. Si on change la notion de distance alors l'allure des géodésique de l'espace peuvent prendre une allure très différente.

Introduction

A l'origine, le terme géodésique vient de géodésie (du grec gaïa " terre " et daiein " partager, diviser "), la science de la mesure de la taille et de la forme de la Terre. La géodesique désignait donc pour des géomètres le chemin le plus court entre deux points de l'espace (sous entendu géographique).

La transposition aux mathématiques fait de la géodésique la généralisation de la notion de " ligne droite " aux " espaces courbes ". La définition de la géodésique dépendant donc du type d'" espace courbe ", l'acceptation précedente n'y est plus vraie que localement dans le cas où cet espace dispose d'une métrique.

Le chemin le plus court entre deux points dans un espace courbe peut être obtenu en écrivant l'équation de la longueur de la courbe, et en cherchant la valeur minimale pour cette valeur. De manière équivalente, on peut définir une autre valeur, l'énergie de la courbe et chercher à la minimiser, ce qui aboutit aux mêmes équations pour une géodésique. Intuitivement, on peut chercher à comprendre cette seconde formulation en imaginant une bande élastique tendue entre deux points, qui, si elle suivait la géodésique, aurait une longueur minimale et donc une énergie minimale.

Les géodésiques sont souvent rencontrées dans le cadre de l'étude de la géométrie riemannienne et plus généralement des géométries métriques. En physique, les géodésiques décrivent le mouvement des particules libres, c'est-à-dire lorsqu'elles ne sont pas soumises à une force externe (autre que la gravitation dans le cadre de la relativité générale); en particulier, le chemin suivi par un rocher en chute libre, un satellite en orbite ou la forme d'une orbite planétaire sont tous décrits par des géodésiques de la théorie de la relativité générale. Par contre la trajectoire d'un spationaute en route pour la Lune dans une fusée n'est pas une géodésique en raison de la force de poussée exercée par le moteur de l'engin.

Exemples

Mathématiques euclidiennes

Les exemples les plus familiers de géodésiques sont les lignes droites en géométrie euclidienne. Sur une sphère, les géodésiques sont les grands cercles. Le chemin le plus court entre un point A et un point B sur une sphère est donné par la plus petite portion du grand cercle passant par A et B. Si A et B sont aux antipodes (comme le pôle Nord et le pôle Sud), il existe une infinité de plus courts chemins.

Géographie

Un repère géodésique (système géodésique) est une façon de repérer un lieu proche de la surface terrestre (par exemple par la latitude et la longitude). C'est un repère en trois dimensions (une planisphère n'en a que deux) dans un repère euclidien.

Si on assimile la Terre à une sphère, les géodésiques sont des arcs de cercle aussi nommées "arcs de grand cercle", ou "orthodromies". Ce n'est qu'une approximation de la réalité, la forme de le Terre étant proche de celle d'un ellipsoïde de révolution.

Physique

Représentation de trois types de géodésique dans un champ de gravitation. La première correspond à un corps initialement au repos et qui tombe directement vers la source du champ de gravitation. La seconde, circulaire, correspond à un corps en orbite, comme une planète autour du Soleil par exemple. La dernière enfin correspond à un corps venant de loin et dont la trajectoire est déviée par la présence d'un champ de gravité. C'est le cas de la lumière d'une étoile passant à proximité du Soleil, c'est l'effet de lentille gravitationnelle.

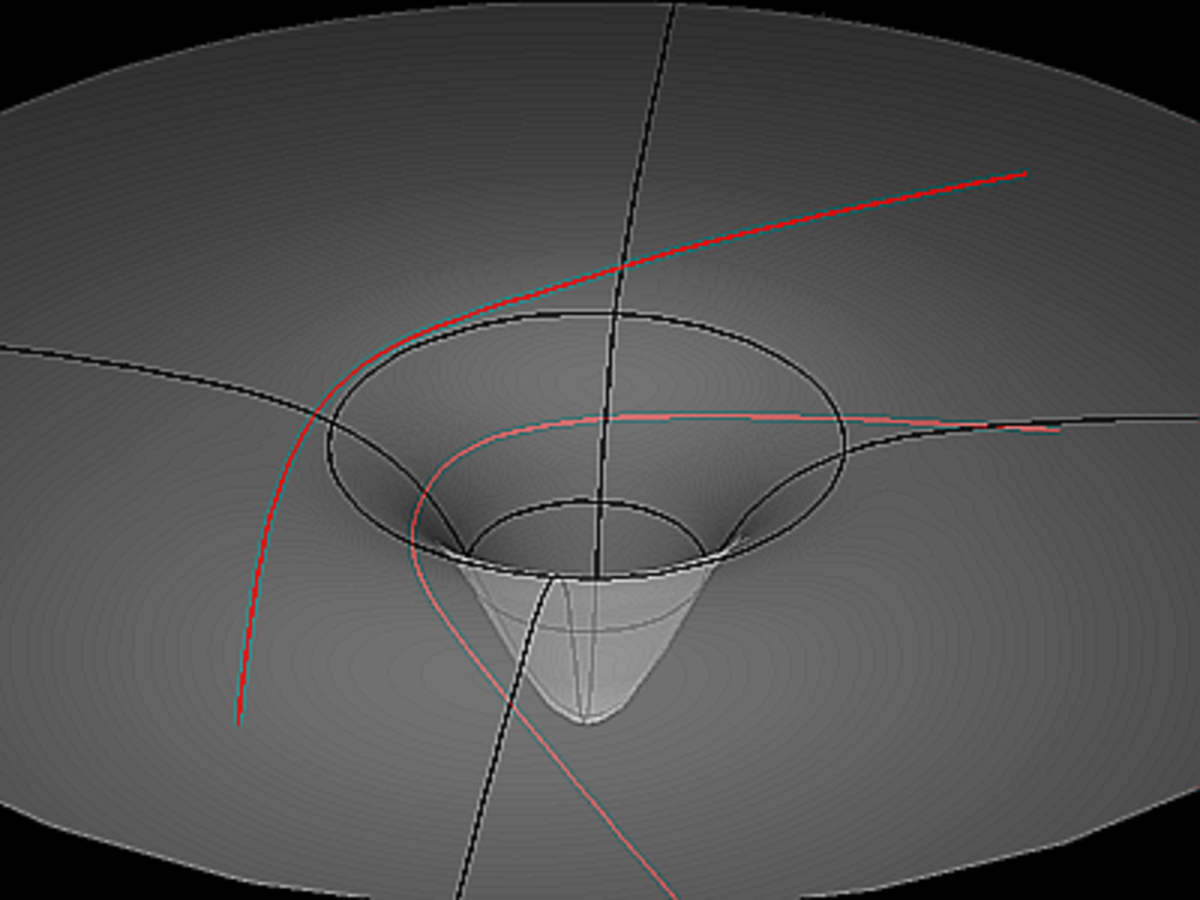
En physique, la géodésique est une généralisation de cette application terrestre. Au lieu d'avoir un obstacle matériel à contourner, il s'agit par exemple d'un champs de force modifiant la trajectoire.

Les sondes Voyager ont, par exemple, suivi un itinéraire spatial courbé (comme sur l'image ci-contre), à chaque passage à proximité d'une planète. Leur trajet, que l'on pourrait comparer à une forme de spirale est pourtant le chemin le plus rapide.

La relativité restreinte d'Einstein, en reliant la matière à l'énergie a permis d'appliquer le concept de géodésique à des éléments qui jusque-là semblaient y échapper, comme la lumière.

Cela se concrétise par exemple en astrophysique par le fait que la présence d'une étoile entre une source de lumière et un observateur courbe le trajet optimal que la lumière doit effectuer pour arriver jusqu'à lui.

La relativité générale, en reliant le temps à un espace courbe à quant à elle permis de lier la notion d'orbite et celle de géodésique.

l'orbite de la terre autour du soleil est alors son chemin logique, dans l'espace temps, qui résulte du mélange de son élan et de sa chute vers le soleil.

Applications géométriques

Géométrie métrique

En géométrie métrique, une géodésique est une courbe suivant partout localement la distance minimale. Plus précisément, une courbe paramétrique γ: I → M depuis l'intervalle unité I vers l'espace métrique M est une géodésique s'il existe une constante v ≥ 0 telle que pour tout t ∈ I il existe un voisinage J de t dans I tel que pour tous t₁, t₂ ∈ J l'on ait :

Ceci généralise la notion de géodésique pour les variétés riemanniennes. Cependant, en géométrie métrique, les géodésiques considérées sont presque toujours équipées d'une paramétrisation naturelle, ce qui se définit par le fait que v = 1 et

Géométrie (pseudo-)riemannienne

Sur une variété pseudo-riemannienne, une géodésique M est définie par une courbe paramétrée régulière γ(t) qui transporte parallèlement son propre vecteur tangent.

Pour comprendre intuititvement ce que cela signifie, on peut imaginer un avion de ligne volant à altitude constante autour de la Terre, allant de Paris à Pékin par le chemin le plus court. Du point de vue des passagers, la direction de l'avion est en permanence la même. À la fin du voyage, les passagers n'ont jamais ressenti d'accélération qui leur aurait fait changer de direction : d'après eux ils ont pris le chemin le plus court. Néanmoins, si on considère le référentiel centré sur la Terre, le vecteur décrivant la vitesse de l'avion a changé de direction au court du temps pour suivre la forme de la planète. Cette modification du vecteur vitesse de l'avion de façon adaptée à la géométrie dans laquelle il se déplace correspond précisément à ce qu'on entend par transport parallèle.

En termes mathématiques, ceci s'exprime de la manière suivante, avec γ(λ) la courbe paramétrée représentant la géodésique et en notant

:

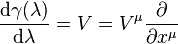
le vecteur tangent à la courbe (le vecteur vitesse si on identifie λ avec le temps dans le référentiel du voyageur) dans le référentiel correspondant aux coordonnées x^μ

où ∇ est la connexion de Levi-Civita sur M (équivalente à la dérivée covariante)

A partir de cette définition et de l'expression en composant de la connexion de Levi-Civita, on obtient l'équation de la géodésique :

Les géodésiques sont donc, dans la variété, des courbes paramétriques répondant à cette équation différentielle. Les sont les symboles de Christoffel, qui dépendent directement du tenseur métrique : ils représentent la déformation infinitésimale de l'espace par rapport à un espace plat.

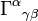
Pour comprendre intuitivement la première formulation, l'opérateur représente l'accélération le long de γ(λ). L'équation géodésique dit donc que l'accélération du vecteur tangent à la courbe le long de la courbe est nulle.