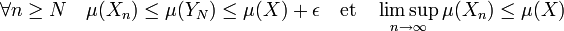Distance de Hausdorff - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
La distance de Hausdorff sur E définit une distance sur l’ensemble K(E) des compacts non-vides de E. K(E) est alors un espace métrique et sa topologie dépend de celle de E.
Si E est un espace complet, alors K(E) est complet. Si E est un espace compact, alors K(E) est compact.
Par conséquent, toute suite
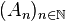
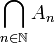
Propriété
La distance de Hausdorff DH(S,T) est nulle si et seulement si S = T et elle augmente lorsque des différences de plus en plus importantes apparaissent entre S et T.
Le calcul de la distance de Hausdorff peut se faire en utilisant une carte de distances.
Comparaison de squelettes
Selon Choi et Seidel, la distance de Hausdorff telle qu'elle est définie n'est pas adaptée à la comparaison de formes par leur squelette pondéré. En effet, la squelettisation est une transformation très sensible aux perturbations apparaissant dans les formes. Même si la distance de Hausdorff de deux formes est très faible (les formes sont très similaires), leurs squelettes respectifs peuvent être très différents. Ainsi, la distance de Hausdorff entre des squelettes peut ne pas correspondre à la similarité de leur formes d'origine.
Afin de résoudre ce problème, Choi et Seidel ont proposé de remplacer la distance euclidienne par la distance hyperbolique dans le calcul de la distance de Hausdorff.
Mesure de similarité: bibliographie
- Sung Woo Choi and Hans Peter Seidel. Hyperbolic Hausdorff distance for medial axis transform. Graphics Models, 63(5):369-384, 2001.
- William Rucklidge. Efficient visual recognition using the Hausdorff distance, LNCS 1173. Springer Verlag, 1996.
Continuité
Ensemble dense


L'existence d'ensembles denses intéresse autant le mathématicien que l'ingénieur en traitement d'images. Pour l'ingénieur, Un sous ensemble dense permet d'approximer n'importe quel point de EH (le terme point désigne un élément de l'ensemble étudié, ici des figures géométriques). Ainsi FH est dense dans EH lorsque pour tout point X de EH et pour tout nombre réel ε strictement positif, il existe un point Y de FH à une distance inférieure à ε de X.
L'ensemble dense est choisi plus petit pour pouvoir être travaillé plus commodément. La figure de droite illustre deux ensembles denses, si E est un espace euclidien, comme le plan pour le traitement d'images. Le premier exemple correspond aux pixels. L'espace est quadrillé par un ensemble de droites (des hyperplans en dimension quelconque) dont les directions sont toutes orthogonales à un vecteur d'une base orthonormale et les droites parallèles entre elles sont régulièrement espacées. Cette grille définit un ensemble de petits carrés (d'hypercubes si la dimension est quelconque), le premier ensemble dense est celui constitué d'un ensemble fini de petits carrés de cette nature. Les ingénieurs parlent d'image matricielle
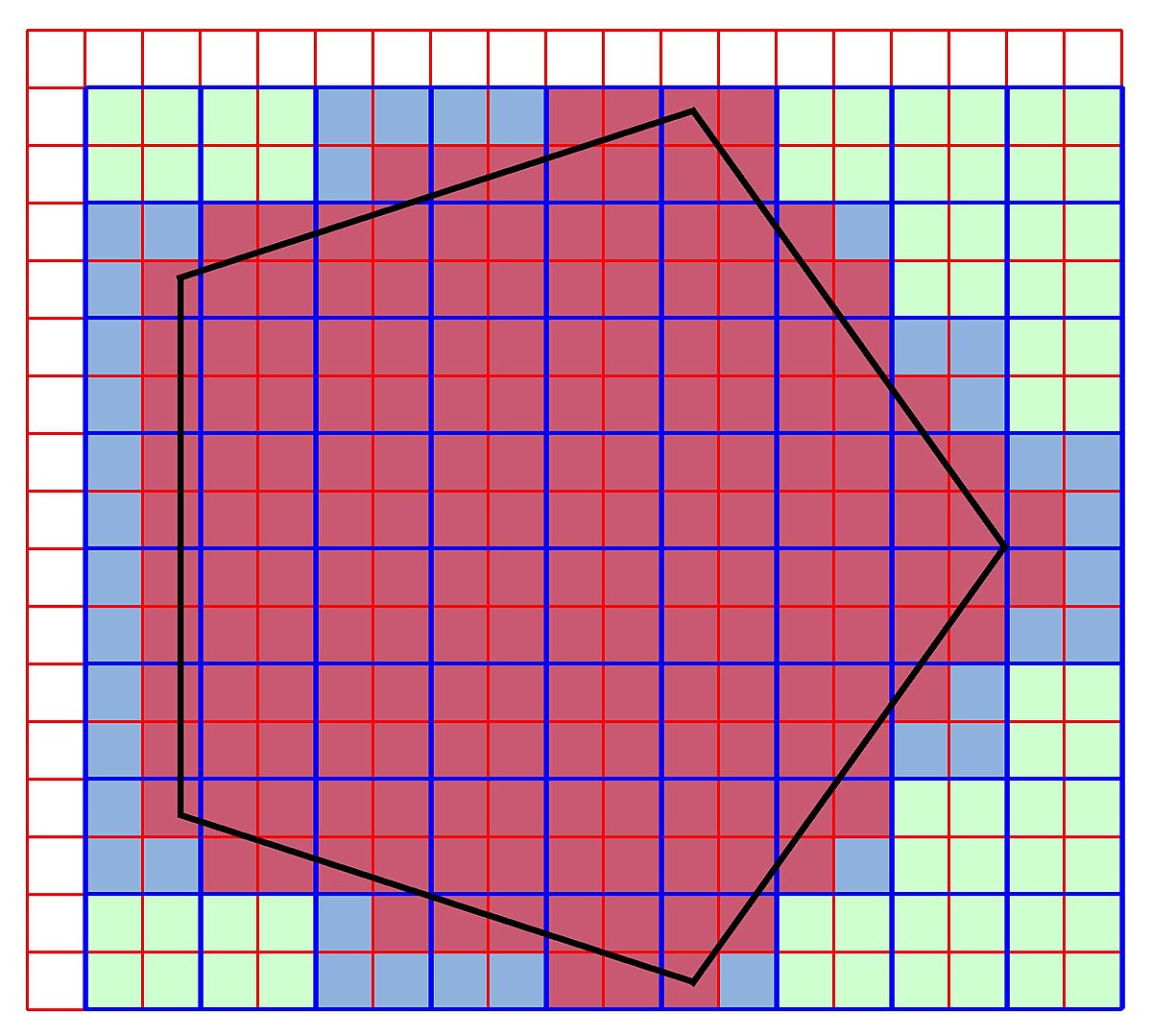
En mathématiques, on choisit souvent le pas de la grille égal à 1/2n, où n est un entier quelconque, il existe ainsi une infinité de tailles de grille possibles, de plus en plus précise à mesure que n augmente. Une forme, par exemple le cercle violet sur la figure de droite, est approximée par ces petits carrés. Un algorithme consiste à sélectionner un petit carré s'il possède une intersection non vide avec la figure qu'il doit approximer.
Une deuxième méthode consiste à choisir comme ensemble dense les polygones, ou encore les polyèdres dans le cas d'une dimension quelconque. Pour un ingénieur, beaucoup moins d'informations sont nécessaire pour décrire une figure géométrique avec cette méthode. Cette approche permet, soit un gain de temps, soit une précision accrue. La deuxième figure de droite est une approximation polygonale, aussi appelée image vectorielle. Pour le mathématicien, les polyèdres forment un ensemble contenant strictement le précédent, il est donc naturel qu'il soit dense, lui aussi.
Il est parfois utile de conserver la convexité, une fois encore, les polyèdres convexes forment un ensemble dense parmi les convexes de EH.
Ici, E désigne un espace euclidien de dimension d. Ici Gn désigne l'ensemble hypercubes fermés de la grille et d'arêtes de longueur 2-n et X désigne un fermé borné de EH. La démonstration est un peu plus riche que celle annoncée dans le paragraphe.
-
- Il existe une suite de polygones (Pn), décroissante pour l'inclusion, tel que Pn contienne X et tel que la distance entre X et Pn soit inférieure à (d/22n)1/2 :
On considère l'ensemble des hypercubes de Gn ayant une intersection non nulle avec X, l'union des éléments de cet ensemble est noté Pn. Deux des ensembles sont illustrés sur la figure de droite. La figure X est un polygone dont la frontière est dessinée en noir. Le premier ensemble illustré correspond aux carrés bleus, le deuxième, deux fois plus fin et qui cache en partie les carrés bleus, est illustré par la couleur rouge.
La décroissance de la suite ainsi que le fait que Pn contienne X sont garantis par construction.
La plus grande distance possible est obtenue si X intersecte un hypercube uniquement en un sommet, le sommet le plus éloigné est le point de Pn le plus éloigné de X, la distance est celle de la plus grande diagonale, égale à (d/22n)1/2.
La distance entre Pn et X tend vers 0, par définition de la limite, 4X est bien celle de la suite des polygones.
-
- Si X est convexe, la suite des enveloppes convexes (Kn) des polygones Pn est une suite décroissante pour l'inclusion, tel que Qn contienne X et tel que la distance entre X et Qn soit inférieure à (d/22n-2)1/2 :
Le raisonnement est le même que le précédent, il suffit de remarquer qu'ajouter une couche de petits cubes construit une figure qui contient l'enveloppe convexe Kn.
Fonctions continues
Si une fonction est continue, ce qu'elle représente est bien conservée par de petites modifications. Un exemple essentiel est la somme de Minkowski. A deux ensembles X et Y, on associe l'ensemble des vecteurs de la forme x + y où x est élément de X et y de Y. En imagerie, sommer une figure avec un petit disque permet d'atténuer les contours. En mathématiques pures, la somme de Minkowski intervient dans de nombreux théorèmes isopérimétriques. Le fait que C soit un compact convexe implique l'égalité C + C = 2C (ce qui n'est pas une évidence, la première partie correspondant à une somme de Minkowski et la deuxième à une homothétie de rapport 2). C'est un élément clé de la démonstration du théorème de Minkowski, utilisé en théorie algébrique des nombres.
Un deuxième exemple est donné par la fonction mesure, si E est un espace euclidien. La mesure de Lebesgue associe à une figure son volume. Elle possède une forme de continuité pour la distance de Hausdorff, elle est semi continue supérieurement. Cela indique que si un algorithme construit une figure à l'aide d'approximations de plus en plus précises, la figure finale possède une mesure qui ne fait pas de saut vers le bas. Mathématiquement, on le modélise par une suite (Xn) de figures qui converge vers une figure X, au sens de Hausdorff. Le volume de la figure X n'est pas beaucoup plus petit que celui de Xn, si n est grand. Si μ désigne la mesure de Lebesgue, c'est-à-dire la fonction qui à une figure associe son volume :
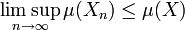
S'il n'existe pas de possibilité de saut vers le bas, il peut y en avoir vers le haut. On peut s'en rendre compte en construisant une image à l'aide d'étapes successives, notées (Xn). On suppose que l'image est composée de pixels trop petits pour être visibles. A chaque étape, l'algorithme ajoute quelques points isolés dans une surface C. Comme ils sont isolés, les images Xn ne contiennent rien de visible dans C tant que n reste petit. En revanche, si n devient très élevé, on peut voir apparaître une surface visible dans C, de mesure non nulle, qui est souvent un artéfact indésirable. Mathématiquement, cela provient du fait qu'il existe un ensemble dénombrable de points, qui forment chacun un ensemble de mesure nulle, dont l'adhérence n'est pas de mesure nulle. On peut prendre par exemple les points de C à coordonnées rationnelles.
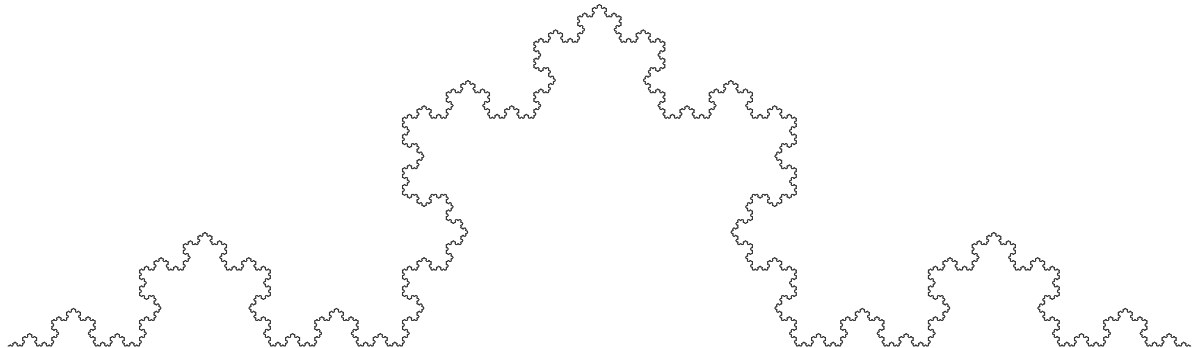
A la différence du volume, la fonction périmètre, ou plus précisément la mesure de la frontière, ne possède aucune continuité. Il est possible de construire deux figures très proches, au sens de Hausdorff, et de périmètres aussi éloignés qu'on le souhaite. A l'aide de la courbe de Koch, il est possible de construire une suite convergente de figures géométriques, dont les périmètres successifs divergent. Cette discontinuité, pour l'ingénieur, signifie qu'un algorithme uniquement fondé sur la distance de Hausdorff risque de ne pas respecter précisément les contours. C'est une des raisons qui poussent à utiliser des distances modifiées.
Ici, E désigne un espace euclidien.
-
-
- La somme de Minkowski est continue:
-
- Soit X et Y deux éléments de EH. L'objectif est de montrer que la somme de Minkowski est continue en (X, Y), c'est-à-dire :

- On choisit η égal à ε/2. Soit x + y un point de X + Y. Il existe un point x1 (resp. y1) de X1 (resp. Y1) à distance inférieure à ε/2 de X (resp. Y). Le point x1 + y1 de X1 + Y1 est nécessairement à une distance inférieure à ε de X + Y. On montre de même que tout point de X1 + Y1 est à une distance inférieure de ε à X + Y, ce qui montre la proposition.
Avant d'étudier la continuité de la mesure de Lebesgue, deux propositions intermédiaires simplifient la démonstration.
-
-
- Une suite de fermés bornés (Xn) de EH, décroissante au sens de l'inclusion, est convergente au sens de Hausdorff. La limite est l'intersection des éléments de la suite :
-
- Soit X l'intersection des éléments de la suite. L'ensemble X est borné, car il est inclus dans un ensemble borné, par exemple X1. L'ensemble est fermé car l'intersection de fermés est un fermé.
- Il ne reste plus qu'à montrer que si ε est un réel strictement positif, il existe un entier N tel que pour tout n plus grand que N, un élément de Xn n'est jamais à une distance plus grande de X que ε. Par contraposé, cela revient à montrer que tout élément y qui est à une distance plus grande de X que ε n'est dans aucun Xn, si n est plus grand que n, ou simplement que y n'est pas dans Yn. Comme y n'est pas dans X et que X est l'intersection des différents Xn, au moins l'un de ces ensembles ne le contient pas. Notons XN, l'un de ceux là, si n est plus grand que N, Xn est inclus dans XN et ne peut contenir y. On en déduit que X contient la limite de la suite (Xn). Réciproquement la limite contient nécessairement X, qui est inclus dans chaque Xn.
Une fois connu le comportement d'une suite décroissante pour l'inclusion, on peut démontrer la convergence de sa mesure.
-
-
- Soit une suite de fermés bornés (Xn) d'éléments mesurables de EH, décroissante au sens de l'inclusion. La limite X est mesurable et la mesure de X est la limite de la suite des mesures de Xn :
-
- X est une intersection dénombrable d'ensembles mesurables, c'est un ensemble mesurable. Considérons la suite de fonctions (χn) de E dans R, où χn est la fonction qui à x associe 0, si x n'est pas élément de X1 ou si x est élément de Xn et 1 sinon. C'est une suite de fonctions croissantes positives et qui converge simplement vers une fonction χ. Le théorème de convergence monotone montre que :
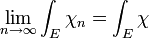
- Ce qui, en termes de mesure ensembliste prend la forme suivante et démontre la proposition :
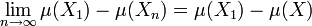
Les deux propositions intermédiaires permettent de conclure. Pour montrer la semi-continuité de la mesure, il suffit de montrer que si une suite Xn de figures mesurables de EH convergent vers une figure X alors la limite supérieure des mesures de Xn ne dépasse pas celle de X. C'est la méthode utilisée dans la démonstration.
-
-
- La mesure de Lebesgue est semi-continue supérieurement:
-
- On commence par construire une suite sur lequel il est possible d'appliquer les deux lemmes. Soit Yn l'adhérence de l'union de tous les Xp pour p supérieur à n. La suite (Yn) est bien une suite décroissante de fermés. Il reste à montrer qu'elle est bornée et que sa limite est bien la figure X. A partir d'un certain rang, tout élément de la suite Xp est inclus dans X + B, où B désigne la boule unité. L'union des Xp, si p dépasse ce rang est borné car X l'est. L'ensemble Yn est une union fini ensembles bornés, les premiers Xp et d'un autre ensemble borné, l'union des Xp, quand p dépasse le rang précédent, Yn est bien borné.
- Montrons que la limite de (Yn) est X. Soit x un élément de X et ε un réel strictement positif. Comme x est élément de l'ensemble X, il existe un N tel que pour tout n plus grand que N la boule de centre x et de rayon ε rencontre Xn. On en déduit que cette boule intersecte tous les éléments de la suite Yn. Cette propriété est vraie pour tout ε, ce qui montre que x est dans l'adhérence de toutes ces unions, et nécessairement dans chaque Yn, ce qui signifie qu'il appartient à l'ensemble limite. Supposons maintenant que y n'est pas dans X, il n'est pas non plus dans son adhérence car X est fermé, il existe un réel ε tel que la boule de centre y et de rayon 2ε ne rencontre pas X. Autrement dit, la boule de centre y et de rayon ε ne rencontre aucun membre d'une section finissante de la suite (Xn). Ceci montre qu'à partir d'un certain rang, y n'est pas dans l'adhérence de l'union de cette section finissante et n'est dans aucun Yn, si n est suffisamment élevé.
- Finalisons la démonstration. On cherche à prouver que, si ε est un réel strictement positif, il existe un entier N tel que si n est un entier plus grand que N, alors la mesure de Xn ne dépasse pas la somme de la mesure de X et de ε. La suite des mesures de Yn est une suite décroissante qui tend vers la mesure de X. A partir d'un certain rang N, elle ne dépasse pas somme de la mesure de X et de ε. Or aucune mesure de Xn ne dépasse celle de YN ce qui termine la démonstration :