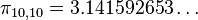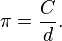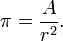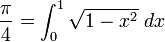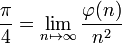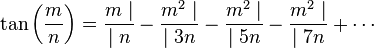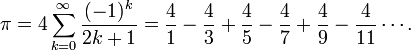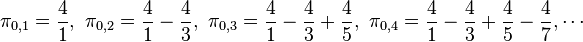Pi - Définition

Introduction

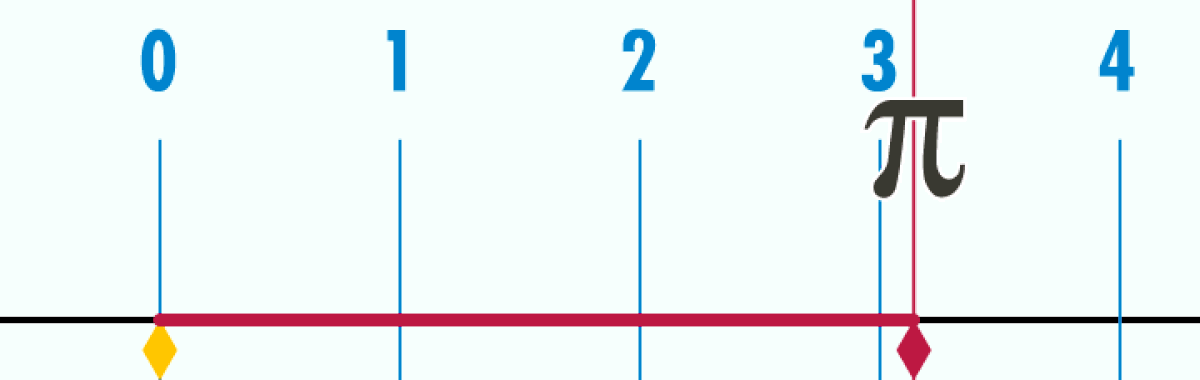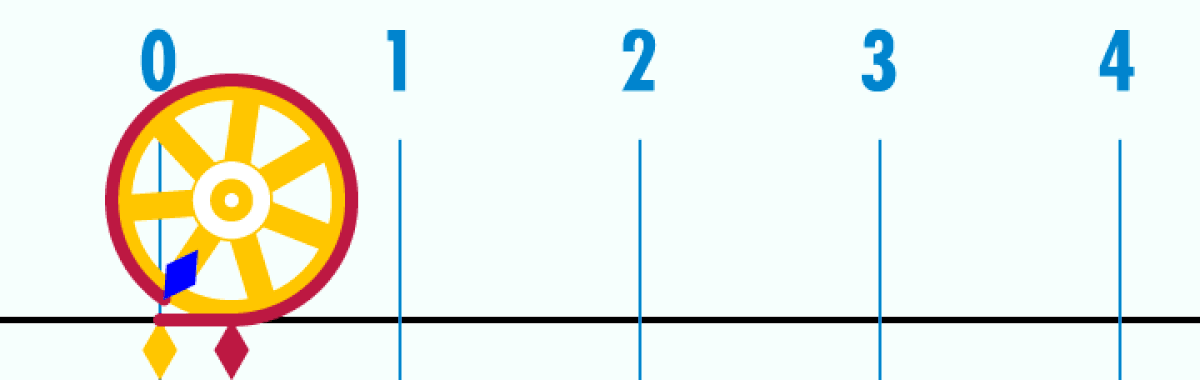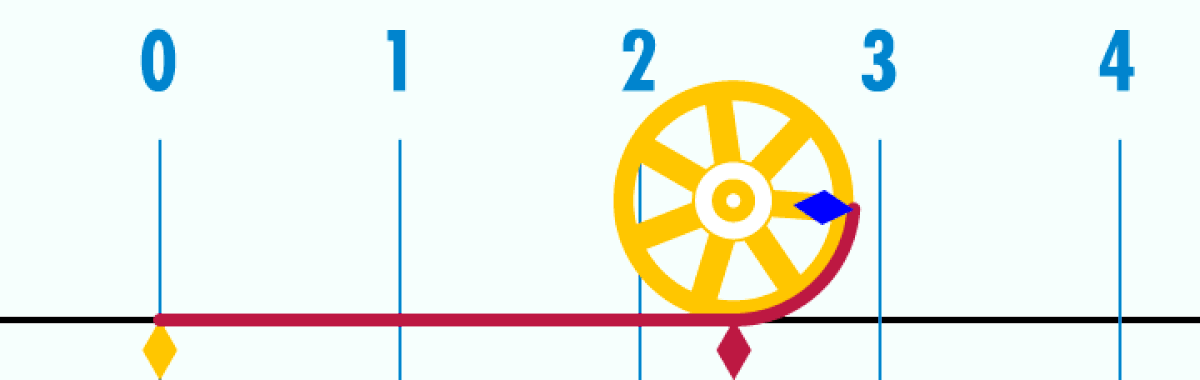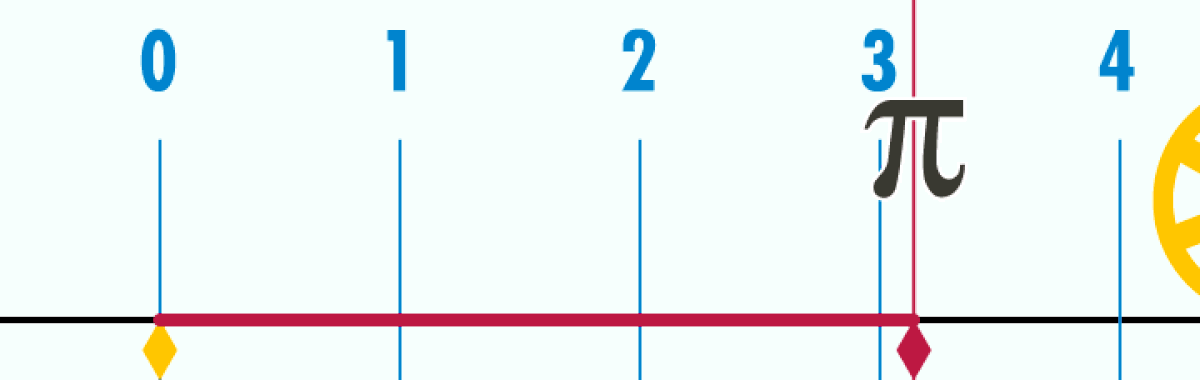
Pi (ou parfois constante d'Archimède) est un nombre, généralement représenté par la lettre grecque du même nom π, et généralement défini comme étant le rapport entre la circonférence d’un cercle quelconque et son diamètre, en géométrie euclidienne. On peut également le définir comme le rapport entre la superficie d'un cercle et le carré de son rayon. La valeur de pi arrondie à 10^^-6 est 3,141593 en écriture décimale. De nombreuses formules, dans des domaines tels que la physique, l'ingénierie et bien sûr les mathématiques, impliquent π, qui est une des constantes les plus importantes des mathématiques.

π est un nombre irrationnel, c'est-à-dire qu'on ne peut pas l'exprimer comme un rapport de deux nombres entiers ; ceci entraîne que son écriture décimale n'est ni finie, ni périodique. C'est aussi un nombre transcendant, ce qui signifie qu’il n'existe pas de polynôme non nul à coefficients entiers dont π soit une racine ; la preuve de ce résultat en 1882 est due à Ferdinand von Lindemann. La détermination d'une valeur approchée suffisamment précise de π et la compréhension de sa nature sont des enjeux qui ont traversé l'histoire des mathématiques ; la fascination exprimée par certains envers ce nombre l'a même fait entrer dans la culture populaire.

L'usage en ce sens de la lettre grecque π, première lettre de « περίμετρος » — périmètre en grec, n'est apparu qu'au XVIII^e siècle.

Définition et premières propriétés

Définition

Dans les dictionnaires et ouvrages généralistes, π est défini comme le rapport constant entre la circonférence d'un cercle et son diamètre (forcément dans le plan usuel qui est le plan euclidien).

Ce rapport ne dépend pas du cercle choisi, en particulier de sa taille. Tous les cercles du plan euclidien sont semblables. Par exemple, si un cercle a le double du diamètre d d'un autre cercle, il aura aussi le double de sa circonférence C.

On démontre que π est aussi le rapport entre la superficie d'un cercle et le carré de son rayon :

Il s'avère que cette définition géométrique, la première historiquement et très intuitive, n'est pas la plus directe pour les mathématiciens quand ils veulent définir π en toute rigueur. Les ouvrages plus spécialisés définissent π par l'analyse réelle à l'aide des fonctions trigonométriques elles-mêmes introduites sans référence à la géométrie (voir plus bas).

Définitions alternatives

Un choix fréquent est de définir π comme le double du plus petit nombre positif x tel que cos(x) = 0. Une autre définition possible est envisageable en considérant les propriétés exp(z+w)=exp(z)exp(w) et exp(0)=1 qui découlent de la définition analytique de l’exponentielle et qui font que l’application est un morphisme de groupes continu du groupe vers le groupe (où est l’ensemble des complexes de module égal à 1). On démontre alors que l’ensemble des nombres réels t tels que exp(it) = 1 est de la forme où a est un réel strictement positif. On pose alors π = a / 2. Le calcul intégral permet ensuite de vérifier que cette définition abstraite correspond bien à celle de la géométrie euclidienne.

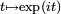
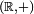
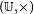
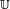
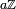
Le groupe Bourbaki propose une définition alternative très voisine en démontrant l’existence d’un morphisme de groupe f continu de vers tel que f(1/4) = i. Il démontre que ce morphisme est périodique de période 1, dérivable et qu’il existe un réel a tel que, pour tout réel x, f'(x) = 2iaf(x). Il définit π comme le réel ainsi trouvé.

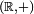
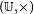
Les deux méthodes précédentes consistent en réalité à calculer le périmètre du cercle, qu'on a défini par la fonction ou la fonction

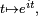
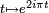
Mais on peut aussi définir π grâce au calcul intégral en posant :

ce qui revient à calculer l’aire d’un quart de disque de rayon 1.

Ou bien à l’aide du dénombrement, en appelant le nombre de couples d’entiers naturels (k, p) tels que et en définissant :

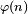
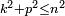
ce qui est une autre méthode pour calculer la surface du quart de disque.

Irrationalité

π est un nombre irrationnel, ce qui signifie qu'on ne peut pas écrire π=p/q où p et q seraient des nombres entiers. Al-Khawarizmi, au IX^e siècle, est persuadé que π est irrationnel. Moïse Maïmonide fait également état de cette idée durant le XII^e siècle. Ce n'est cependant qu'au XVII^e siècle que Johann Heinrich Lambert prouve ce résultat.

C'est en 1761 que ce dernier étudie, dans son ouvrage « Mémoires sur quelques propriétés remarquables des quantités transcendantes, circulaires et logarithmiques », le développement en fraction continue de la fonction trigonométrique tan et montre que le développement en fraction continue de tan(m/n), avec m et n des nombres entiers non nuls, est illimité. Il s'écrit plus précisément

Or, on sait qu’un nombre dont le développement en fraction continue est illimité est irrationnel, donc quand x est un rationnel non nul, tan(x) est irrationnel. Or, tan(π/4) vaut 1, c’est un rationnel. Par contraposée, on prouve que π/4, et donc π, n’est pas rationnel.

Au cours du XX^e siècle, d'autres démonstrations furent trouvées, celles-ci ne demandant pas de connaissances plus avancées que celle du calcul intégral. L'une d'entre elles, due à Ivan Niven, est très largement connue. Une preuve similaire avait été trouvée quelques temps auparavant par Mary Cartwright.

Transcendance

π est aussi un nombre transcendant, c'est-à-dire qu'il n'existe pas de polynôme à coefficients rationnels dont π soit une racine.

C'est au XIX^e siècle que ce résultat est démontré. En 1873, Charles Hermite prouve que la base du logarithme népérien, le nombre e, est transcendant. En 1882, Ferdinand von Lindemann généralise son raisonnement en un théorème (le Théorème d'Hermite-Lindemann) qui stipule que, si x est algébrique et différent de zéro, alors e^x est transcendant. Or e^iπ = -1 donc e^iπ n’est pas transcendant. Par contraposée, iπ n’est pas algébrique et π est transcendant.

Une conséquence importante de la transcendance de π est que celui-ci n'est pas constructible. En effet, le théorème de Wantzel énonce en particulier que tout nombre constructible est algébrique. En raison du fait que les coordonnées de tous les points pouvant se construire à la règle et au compas sont des nombres constructibles, la quadrature du cercle est impossible ; autrement dit, il est impossible de construire, uniquement à la règle et au compas, un carré dont la superficie serait égale à celle d'un cercle donné.

Représentation décimale

Les 100 premiers chiffres de l'écriture décimale de π sont :

3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 307 816 406 286 208 998 628 034 825 342 117 067 , puis voir pour plus de décimales.

Alors qu'en 2007, on connaît plus de 10¹² décimales de π, de nombreuses applications n'ont besoin que d'une dizaine de chiffres, comme l'estimation de la circonférence d'un cercle. Par exemple, la représentation décimale de π tronquée à 39 décimales est suffisante pour estimer la circonférence d'un cercle dont les dimensions sont celles de l'univers observable avec une précision comparable à celle du rayon d'un atome d'hydrogène.

Étant donné que π est un nombre irrationnel, sa représentation décimale n'est pas périodique et ne prend pas fin. La séquence des décimales de π a toujours fasciné les mathématiciens et les amateurs, et beaucoup d'efforts ont été mis en œuvre afin d'obtenir de plus en plus de décimales et d'en rechercher certaines propriétés. Malgré les importants travaux d'analyse effectués et les calculs qui ont réussi à déterminer plus de 200 milliards de décimales de π, aucun modèle simple n'a été trouvé pour décrire la séquence de ces chiffres. Les chiffres de la représentation décimale de π sont disponibles sur de nombreuses pages web, et il existe des logiciels de calcul des décimales de π qui peuvent en générer des milliards et qu'on peut installer sur un ordinateur personnel.

Par ailleurs, le développement décimal de π ouvre le champ à d’autres questions, notamment celle de savoir si π est un nombre normal, c'est-à-dire que ses chiffres en écriture décimale sont équirépartis. On peut aussi se demander si π est un nombre univers, ce qui signifie qu'on peut trouver dans son développement décimal n’importe quelle séquence de chiffres. En 2006, il n'existe pas de réponse à ces questions.

Représentation fractionnaire

Les fractions de nombres entiers suivantes sont utilisées pour mémoriser ou approximer Pi dans des calculs (nombre de chiffres significatifs entre parenthèses): 3 / 1 (1); 22 / 7 (3); 333 / 106 (5); 355 / 113 (7); 103993 / 33102 (9); 104348 / 33215 (10); 208341 / 66317 (10), à comparer à PI=3,141 592 653 589 793 238 462 ...

Voir ci dessous pour d'autres approches fractionnaires (Histoire,Approximation numérique, fractions continues et Pi#Mémorisation de π).

Approximation de π

On peut trouver une valeur approchée de π de façon empirique, en traçant un cercle, puis en mesurant son diamètre et sa circonférence, puis en divisant la circonférence par le diamètre. Une autre approche géométrique, attribuée à Archimède, consiste à calculer le périmètre P_n d'un polygone régulier à n côtés et à mesurer le diamètre d de son cercle circonscrit, ou celui de son cercle inscrit. Plus le nombre de côtés du polygone est grand, meilleure est la précision obtenue pour la valeur de π.

Archimède a déterminé la précision de cette approche en comparant les résultats obtenus par la formule en utilisant deux polygones réguliers ayant le même nombre de côtés, et pour lesquels le cercle est pour l'un cercle circonscrit, et pour l'autre cercle inscrit. Il a réussi, avec un polygone à 96 côtés, à déterminer que 3 + ¹⁰⁄₇₁ < π < 3 + ¹⁄₇.

On peut également obtenir des valeurs approchées de π en mettant en œuvre seulement des méthodes purement mathématiques. La plupart des formules utilisées pour calculer π se basent sur ses propriétés mathématiques et demandent pour les comprendre des connaissances en trigonométrie et en calcul intégral. Cependant, certaines n'ont pas ce défaut, comme la formule de Leibniz :

Cette série converge si lentement que près de 300 termes sont nécessaires pour calculer π à 2 décimales près. Cependant, il est possible de définir une suite similaire qui converge vers π beaucoup plus rapidement, en posant

et en définissant :

.

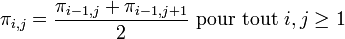
Le calcul de π_10,10 demande alors un temps similaire à celui requis pour calculer les 150 premiers termes de la série initiale, mais la précision est bien meilleure car approche π à 9 décimales près.