Dynamique des fluides - Définition
La dynamique des fluides est l'étude des mouvements des fluides, qu'ils soient liquide ou gaz. La résolution d'un problème de dynamique des fluides demande normalement de calculer diverses propriétés des fluides comme par exemple la vitesse, la pression, la densité et la température en tant que fonctions de l'espace et du temps.
Perspectives actuelles
On connaît parfaitement les équations qui gouvernent les fluides : il s'agit des équations de Navier-Stokes, ou des dérivés. Mais à l'heure actuelle, le problème ne se situe plus là. Malgré leur (relative) simplicité, ces équations peuvent générer des comportements extrêmement complexes, comme la turbulence. On ne peut aborder ces phénomènes chaotiques que d'un point de vue statistique, en utilisant un arsenal de méthodes théoriques (bases de filtres, fractales…) - mais il reste difficile de prévoir à partir des équations, les comportements fins de la turbulence. Or la très grande majorité des écoulements qui nous entourent (eau, air) sont turbulents - c'est dire l'importance pratique de ce problème.
Il est également intéressant d'étudier la transition entre un comportement simple des fluides (écoulement laminaire) et un comportement chaotique (écoulement turbulent).
Étude des phénomènes
L'étude de ces phénomènes est aujourd'hui bien souvent numérique : on simule des solutions des équations, qui ressemblent effectivement à des écoulements réels - sauf que c'est comme si on disposait d'un système de mesure parfait, qui pourrait tout mesurer sans rien perturber.
Une autre voie de recherche très utilisée est l'étude en soufflerie. En mettant un modèle à étudier dans un fort flux d'air, et en étudiant l'écoulement par divers moyens (mesure de la vitesse d'écoulement par anémomètre ou tube de Pitot, mesure des efforts par des dynamomètres, visualisation des lignes de courant), on peut faire de nombreux calculs et améliorer les paramètres aérodynamiques de l'objet).
Parallèlement, les études d'hydrodynamique sur les navires, les installations pétrolières en mer ou les ouvrages portuaires utilisent souvent des bassins dans lesquels on peut représenter des vagues réalistes. Comme en soufflerie, les essais s'effectuent généralement sur un modèle réduit.
Cela pose donc, dans les deux cas, des problèmes de similitude qui nécessitent d'abord une analyse critique des phénomènes pour mettre en évidence les paramètres pertinents et ceux que l'on peut négliger, ensuite leur prise en compte à l'aide de nombres sans dimension.
Il existe également d'autres méthodes expérimentales pour étudier des écoulements: strioscopie, Laser-Doppler, …
Applications de la dynamique des fluides
La dynamique des fluides et ses sous-disciplines comme l'aérodynamique, l'hydrodynamique, et l'hydraulique ont des applications très diverses. Par exemple, elles sont utilisées dans le calcul des forces et des moments dans l'aéronautique ou pour les prévisions météorologiques.
Le concept de fluide est étonnamment général. Par exemple, certains des concepts mathématiques de base concernant la gestion du trafic sont dérivés en considérant le trafic comme un fluide continu.
L'hypothèse de la continuité
Les gaz sont composés de molécules qui se heurtent entre elles comme des objets pleins. L'hypothèse de continuité, cependant, considère les fluides comme étant continus. C'est-à-dire que l'on admet que des propriétés telles que la densité, la pression, la température, et la vitesse sont prises pour étant bien définies a des points infiniment petits, et ne changent pas d'un point à l'autre. La nature discrète et moléculaire d'un fluide est donc ignorée.
Ces problèmes pour lesquels l'hypothèse de continuité ne donne pas des réponses avec l'exactitude désirée sont résolus grâce à la mécanique statistique. Afin de déterminer s'il faut employer la dynamique liquide conventionnelle (une sous-discipline de la mécanique des milieux continus) ou de la mécanique statistique, le nombre de Knudsen est évalué pour résoudre le problème. Les problèmes pour lesquels le nombre de Knudsen est égal ou supérieur à 1 doivent être traités par la mécanique statistique pour donner des réponses fiables.
Équations de la dynamique des fluides
Les axiomes fondamentaux de la dynamique des fluides sont les lois de conservation comme la conservation des masses, la conservation de la quantité de mouvement (plus connu sous le nom de seconde loi de Newton), et la conservation de l'énergie. Cela constitue la base de la mécanique newtonienne et sont aussi importantes en mécanique relativiste.
Les équations les plus importantes sont les équations de Navier-Stokes, qui sont des équations différentielles non-linéaire décrivant le mouvement des fluides. Ces équations, lorsqu'elles ne sont pas simplifiées n'ont pas de solutions analytiques et ne sont donc utiles que pour des simulations numériques. Ces équations peuvent être simplifiées de diverses manières ce qui rend les équations plus facile à résoudre. Certaines simplifications permettent de trouver des solutions analytiques à des problèmes de dynamique des fluides.
Choix d'une description du fluide
Pour décrire mathématiquement les propriétés d'un fluide en mouvement, deux systèmes cohabitent, l'un et l'autre présentant des avantages dans des situations particulières. Il s'agit de la description lagrangienne et de la description eulérienne. Tandis que la première consiste à observer les modifications des propriétés d'une particule fluide que l'on suit dans son mouvement, la seconde se place en un point fixe du milieu à l'étude et observe les modifications des propriétés du fluide qui défile en ce point. Les deux descriptions sont liées mathématiquement par la relation :
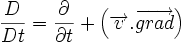
Où le terme
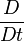
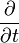
Flux compressible et incompressible
Un fluide est appelé compressible si les changements de la densité du fluide ont des effets significatifs sur l'ensemble de la solution. Dans le cas contraire, il s'agit d'un fluide incompressible et les changements de densité sont ignorés.
Afin de savoir si le fluide est compressible ou incompressible, on calcule le nombre de Mach. Approximativement, les effets de la compression peuvent être ignorés pour les nombres de Mach en dessous de 0,3. Presque tous les problèmes impliquant des liquides se trouvent dans cette catégorie et sont définis comme incompressibles.
Les équations de Navier-Stokes incompressible sont des simplifications des équations de Navier-Stokes dans lesquelles la densité est considérée comme constante. Elles peuvent être utilisées pour résoudre les problèmes impliquant des fluides incompressibles.
En acoustique, la vitesse du son dans l'air étant finie, le fluide " air " doit être traité comme compressible. En effet, supposons que l'air soit un fluide incompressible, alors il se déplacerait en bloc et propagerait toute modification de pression locale à une vitesse infinie. La vitesse du son c dans un fluide compressible s'écrit d'ailleurs comme fonction de sa compressibilité χ :
c2 = (ρ0χ) − 1
La viscosité
Les problèmes dus à la viscosité sont ceux dans lesquels les frottements du fluide ont des effets significatifs sur la solution. Dans le cas où les frottements peuvent être négligé, le fluide est appelé non-visqueux.
Le nombre de Reynolds peut être employé pour estimer quel type d'équation est approprié pour résoudre un problème donné. Un nombre de Reynolds élevé indique que les forces d'inertie sont plus importante que les forces de frottement. Cependant, même lorsque le nombre de Reynolds est élevé, certains problèmes nécessitent de prendre en compte les effets de la viscosité. En particulier, dans les problèmes où l'on calcule les forces exercées sur un corps (comme les ailes d'un avion), il faut prendre en compte la viscosité. Comme illustré par le paradoxe d'Alembert, un corps immergé dans un fluide non visqueux n'est soumis à aucune force.
Les équations normalement utilisées pour l'écoulement d'un fluide non visqueux sont les équations d'Euler. Dans la dynamique des fluides numérique, on emploie les équations d'Euler lorsqu'on est loin du corps et équations tenant compte de la couche limite lorsqu'on est à proximité du corps.
Les équations d'Euler peuvent être intégrées le long d'une ligne de flux pour aboutir à l'équation de Bernoulli. Quand l'écoulement est partout irrotationnel et non visqueux, l'équation de Bernoulli peut être employée pour résoudre le problème.
Écoulement constant et non constant
Une autre simplification des équations de la dynamique des fluides est de considérer toutes les propriétés du fluide comme étant constantes dans le temps. Ceci s'appelle alors un flux stationnaire et est applicable à de nombreux problèmes, tels que la poussé ou la traînée d'une aile ou un flux traversant un tuyau. Dans le cas particulier d'un flux stationnaire, les équations de Navier-Stokes et d'Euler se simplifient donc.
Si un fluide est à la fois incompressible, non visqueux et stationnaire, il peut être résolu avec l'écoulement potentiel découlant de l'équation de Laplace. Les problèmes de cette classe ont des solutions qui sont des combinaisons d'écoulements linéaires élémentaires.
Lorsqu'un corps est accéléré dans un fluide, s'introduit la notion de masse ajoutée.
Écoulement laminaire et turbulence
La turbulence est un écoulement dominé par des remous, et un aspect aléatoire apparent. Lorsqu'il n'y a pas de turbulences on dit que l'écoulement est laminaire.
La turbulence des fluides obéit à l'équation de Navier-Stokes. Cependant, les problèmes d'écoulement sont si complexes qu'il n'est pas possible actuellement de les résoudre numériquement en partant des principes de base. La turbulence est plutôt modélisée à l'aide d'un des nombreux modèles de turbulence et couplée avec un résolveur de flux qui suppose que le flux est laminaire en dehors de la région de turbulence. L'étude du Nombre de Reynolds permet de déterminer le caractère turbulent ou laminaire d'un écoulement.
Autres approximations
Il y a un grand nombre d'autres approximations possibles faces aux problèmes de la dynamique des fluides. Un écoulement de Stokes est l'écoulement d'un fluide dont le Nombre de Reynolds est très bas, de sorte que les forces d'inertie peuvent être négligées face aux forces de frottement. L'approximation de Boussinesq néglige les forces de compression excepté pour calculer les forces de flottabilité.

















































