Théorie algébrique des nombres - Définition

Théorie algébrique classique des nombres

Entier algébrique

Pour définir de manière générale ces ensembles, il est utile de considérer le plus petit ensemble K contenant les nombres rationnels, toutes les racines d'un polynôme à coefficients rationnels et stable pour l'addition et la multiplication. Une telle structure est appelée corps de décomposition du polynôme. L'anneau considéré, souvent noté O_K est celui des éléments de K qui sont aussi racines d'un polynôme à coefficients entiers et dont le monôme de plus haut degré possède un coefficient égal à 1. Ces nombres sont dits entiers algébriques et l'ensemble est nommé fermeture algébrique de K. Ces deux structures sont un peu analogues aux rationnels et entiers relatifs. Le deuxième ensemble O_K possède des éléments qui n'ont pas d'inverse pour la multiplication, à part quelques exceptions comme 1 et -1 pour les entiers relatifs. Ces exceptions forment une structure multiplicative appelée groupe des unités. Le corps K peut être vu comme composé de fractions d'entiers algébriques et tout élément excepté zéro possède un inverse pour la multiplication. Un corps quadratique correspond à une incarnation des plus simples de cette situation, le polynôme est de degré deux. Les fermetures algébriques ne ressemblent pas toujours à Z. Deux obstructions éloignent la nouvelle structure de la configuration d'origine.

L'ensemble des éléments inversibles de O_K peut devenir vaste. Un exemple est donné par l'étude de l'entier de Dirichlet dont le groupe des unités est infini. Pour tous ces éléments, les outils comme le lemme d'Euclide, l'identité de Bézout ou la décomposition en facteurs premiers s'avèrent inopérants. Dirichlet parvient à élucider la structure de ce groupe à travers le théorème dit des unités de Dirichlet. Pour les corps quadratiques, cette difficulté se traduit par l'équation de Pell-Fermat.

La deuxième obstruction provient du fait qu'il n'existe plus assez de nombres premiers pour assurer une décomposition unique. Par exemple sur l'anneau des entiers de la forme a + i√5.b, le nombre 6 admet deux factorisations différentes :

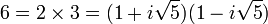
Pourtant aucun des quatre entiers algébriques utilisés ne contient de diviseurs autres qu'eux-mêmes et 1 (à un facteur du groupe des unités près). Un contournement est imaginé par Ernst Kummer, il propose d'adjoindre des nombres idéaux pour obtenir à nouveau une factorisation unique. Plus tard, Richard Dedekind formalise la notion d'idéal généralisant cette idée à tous les anneaux. Les fermetures algébriques possèdent un jeu de propriétés formalisé par les axiomes définissant l'anneau de Dedekind. Pour une telle structure, à chaque nombre est associé son idéal, qualifié de principal et il existe des idéaux qui ne sont associés à aucun nombre. Les idéaux disposent d'une addition et surtout d'une multiplication. De même que les entiers se généralisent en nombres rationnels, la définition d'un idéal s'étend à celle d'idéal fractionnaire qui possède un inverse s'il est non nul. Cette généralisation confère une structure de groupe multiplicatif à l'ensemble. Le groupe des idéaux fractionnaires possède un sous-groupe particulier, celui des idéaux fractionnaires principaux, correspondant aux vrais nombres de K. Le quotient du groupe par ce sous-groupe, opération analogue à celle utilisée en arithmétique modulaire, permet de mesurer le volume des nombres premiers manquants. Le théorème permettant de contourner la deuxième obstruction décrit une propriété de ce groupe quotient, appelé groupe des classes d'idéaux. Il possède un nombre fini d'éléments.

Théorie classique de Galois

D'autres questions, ne portant pas sur les nombres entiers, imposent une généralisation de la notion de nombre. La diagonale d'un carré de côté de longueur un ne s'exprime pas comme une fraction. Elle amène à l'étude d'un nouveau nombre, initialement perçu comme une longueur et égale à la racine carrée de deux. De manière plus générale, l'étude des équations polynomiales introduit des nombres comme l'unité imaginaire ou des racines n^ièmes de rationnels, appelées radicaux. Certaines méthodes comme celles de Cardan ou de Ferrari permettent la résolution par radical de toute équation de degré strictement inférieur à cinq.

Un nombre algébrique est défini comme une racine d'un polynôme. Evariste Galois étudie les propriétés de symétrie de telles racines et met en évidence l'existence d'un groupe fini dit de Galois. En terme moderne, le cadre d'étude est celui d'une extension finie L d'un corps K, c'est-à-dire d'un corps L contenant un corps K et de dimension finie s'il est considéré comme un espace vectoriel sur K. Le groupe de Galois est le groupe des automorphismes de L laissant K invariant. Un exemple est donnée par le plus petit corps contenant toutes les racines d'un polynôme ainsi que ses coefficients. Le groupe de Galois permet une expression générale du théorème d'Abel donnant une condition nécessaire et suffisante pour qu'une équation soit résoluble par radicaux.

La théorie classique de Galois s'appuie sur deux théorèmes, celui de l'élément primitif et celui dit fondamental. Le premier suppose une propriété sur le polynôme minimal d'un élément a de L. Le polynôme minimal de a est le polynôme à coefficients dans K de plus petit degré, unitaire et admettant a pour racine. La théorie montre que dans une extension finie, un tel polynôme existe toujours. Une configuration fréquente indique qu'un polynôme minimal n'admet jamais de racine multiple. Si tel est le cas, l'extension est dite séparable. Le théorème de l'élément primitif indique qu'une extension finie séparable contient toujours un élément p, dit primitif tel que L est le plus petit corps contenant K et p. Si l'extension est séparable et si le groupe de Galois contient autant d'éléments que la dimension de L en tant qu'espace vectoriel, l'extension est dite galoisienne. Dans une telle extension, les sous-corps de L contenant K sont en bijection avec les sous-groupes du groupe de Galois. L'analyse des propriétés de cette bijection est le contenu du théorème fondamental de cette théorie.

Cette approche structurelle, souvent considérée comme l'origine de l'algèbre moderne, dépasse le cadre de l'étude de la résolution d'équations polynomiales. Avant les travaux de Galois, Carl Friedrich Gauss avait compris certains éléments de la théorie, ce qui lui permet de trouver un nouveau polygone régulier constructible à la règle et au compas. Il contient dix-sept sommets (cf l'article Polynôme cyclotomique). La théorie classique des entiers algébriques utilise fréquemment les outils de cette théorie. Le calcul de grandeur comme la norme d'un entier ou le discriminant d'un anneau peut s'exprimer à l'aide du groupe de Galois. Cette propriété est à l'origine de nombreuses démonstrations comme celle du théorème des unités de Dirichlet.