Extension algébrique - Définition
En mathématiques et plus particulièrement en algèbre, une extension algébrique L sur un corps K est une extension de corps dans laquelle tous les éléments sont algébriques sur K c’est-à-dire sont racines d'un polynôme non nul à coefficients dans K. Dans le cas contraire, l'extension est dite transcendante.
Cette approche permet dans un premier temps de pallier les insuffisances de certains corps, par exemple celui des Nombres réels quant aux solutions des équations polynômiales. Elle offre enfin une structure adaptée pour mieux comprendre la structure d'un corps. Les extensions algèbriques sont le support des analyses qui permettent par exemple de résoudre les problèmes de l'antiquité comme la Duplication du cube ou la résolution d'équations polynômiales par radicaux décrit dans le théorème d'Abel.
Motivations
La première formalisation de la notion d'extension algébrique provient d'une tentative par Ernst Kummer (1810-1893) de démonstration du dernier théorème de Fermat. Un article de 1846 définit la notion de nombre idéal qui aboutira à la définition de Richard Dedekind (1831-1916) du concept d'idéal en 1871. Kummer analyse les propriétés d'une extension algébrique engendrée par une racine de l'unité, ce qu'on appelle aujourd'hui extension kummerienne. La formalisation définitive est publiée en 1857[1]. Cet outil permet par exemple de prouver le théorème de Fermat pour une certaine classe de nombres premiers, les nombres premiers réguliers, qui comprend tous les premiers plus petits que 100, à l'exception de 37, 59 et 67 (et bien sûr 2).
Cette démarche consiste à définir des structures algébriques abstraites comme les groupes, les anneaux les corps ou les espaces vectoriels. Elle s'inscrit dans une mouvement qui démarre avec les travaux d'Évariste Galois (1811-1832) où est définie la première structure abstraite : celle des groupes[2]. Ces travaux sont à l'origine de l'algèbre moderne. Les travaux de Kummer prennent tout leur sens comme complément de ceux de Galois, et une extension algébrique particulièrement importante est l'extension de Galois. Les propriétés générales de ces structures permettent de résoudre des problèmes de géométrie, d'arithmétique ou d'algèbre ouverts depuis longtemps.
En géométrie, trois des quatre grands problèmes de l'antiquité sont résolus à l'aide de cette approche. Ils proviennent tous de constructions à l'aide de la rêgle et du compas. On y trouve la trisection de l'angle, la duplication du cube et la constructibilité des polygones réguliers. Toute démonstration moderne de ces trois propriétés utilise l'algèbre abstraite et la notion d'extension algébrique. À la fin du XIXe siècle l'intégralité de la géométrie est fondée sur des structures algébriques abstraites.
En arithmétique, les tentatives de démonstration du dernier théorème de Fermat sont à l'origine des plus nombreuses avancées. La formalisation de la notion d'extension algébrique devient indispensable pour de nombreuses valeurs de n (le paramètre de l'équation de Fermat). Cette structure permet de marier les différentes structures abstraites pour établir les théorèmes. Une extension algébrique est un espace vectoriel, c'est aussi un corps, il est défini grâce à une structure d'anneau euclidien et un groupe opère naturellement sur ce corps. L'extension algébrique devient alors la structure de base de la théorie algébrique des nombres.
En algèbre, l'extension algébrique est la structure de base de la résolution d'un vieux problème, celui de la résolution d'une équation polynômiale à l'aide de radicaux. Si la structure clé est celle de groupe fini, initialement mis en évidence comme un sous-groupe de permutations, elle apparaît plus simple et plus naturelle dans sa formalisation moderne. Le groupe est alors un groupe fini opérant sur une extension algébrique.
Approche par l'exemple
Une extension simple construite à l'aide d'un sur-corps
L'idée est de construire le plus petit sur-corps L de

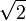
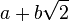

On montre facilement que l'ensemble K de ces éléments s'écrivant
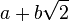

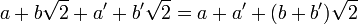
Les éléments neutres de l'addition et de la multiplication sont clairement élément de l'ensemble.
Tout élément possède dans K un opposé:
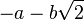
Le produit (c'est là la seule finesse) est aussi stable par la multiplication.
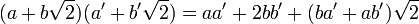
Enfin, tout élément non nul de K admet un inverse:
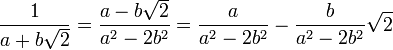
remarque : pour a et b rationnels non tous les deux nuls a² - 2b² est non nul car
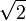
Par construction, ce corps est le plus petit sous-corps des nombres réels contenant à la fois les nombres rationnels et
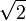
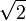
L possède un certain nombre de propriétés intéressantes:
- L est un espace vectoriel sur les nombres rationnels. Cet espace est de dimension finie égale à 2. On parle alors d'extension quadratique.
- L, en tant qu'espace vectoriel possède une base constituée de puissances de
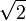
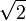
- Si x est un élément de L alors la famille (1, x, x2) est liée car de cardinal supérieur à celui de la dimension. Il existe donc un polynôme à coefficients dans les nombres rationnels ayant x pour racine.
Une approche intuitive montre qu'une structure de type L est un candidat intéressant pour bâtir une théorie. En revanche, il n'est pas très satisfaisant d'avoir utilisé un sur-corps des nombres rationnels, à savoir les nombres réels, pour une telle construction. Si, dans la pratique, quel que soit le corps K il est toujours possible de montrer l'existence d'un sur-corps Ω possèdant les propriétés nécessaires, il existe une autre approche qui ne nécessite pas l'existence d'un tel sur-corps a priori.
Construction à l'aide des polynômes
On démontre que l'ensemble des polynômes à coefficients dans

![\mathbb{R}[X]](https://static.techno-science.net/illustration/Definitions/autres/5/5e11093b37fd30fbaa413f6bdf9647c4_bf95e896a54c240387ad57c91bfa743b.png)

![P_1[X] - P_2[X] = S[X]\times P[X]](https://static.techno-science.net/illustration/Definitions/autres/1/1ee7c0b952d5d357132035efa9615c87_0882c9aeccb30f49b679c6f36e0eab80.png)
Cette congruence est une relation d'équivalence
![\mathbb{R}[X]](https://static.techno-science.net/illustration/Definitions/autres/5/5e11093b37fd30fbaa413f6bdf9647c4_bf95e896a54c240387ad57c91bfa743b.png)
![L = \mathbb{R}[X]/P[X]](https://static.techno-science.net/illustration/Definitions/autres/c/ca782e1b5d89d6d83e383287257d82f7_1d1f8f90655fb41c1c122600b363adaa.png)

Si P[X] est choisi comme étant égal à X2-2 et si le corps est choisi égal à celui des nombres rationnels, on obtient une extension des rationnels isomorphe au sous-corps des nombres réels du paragraphe précédent.
Définitions et premières propriétés
Soit K un corps et L une extension de corps.
-
- Un élément l de L est dit algébrique sur K si et seulement si il existe un polynôme non nul à coefficients dans K ayant l pour racine.
-
- L'extention L est dite algébrique si et seulement si tout élément de L est algébrique sur K.
-
- L dispose d'une structure d'espace vectoriel sur K. Si cette structure confère à L une structure d'espace vectoriel de dimension finie, on parle alors d' extension finie. La dimension est souvent notée [L:K]
-
- S'il existe un élément l de L tel que les puissances de l forment une famille génératrice de L alors l'extension est dite simple.
-
- L'ensemble F des nombres algébriques de L sur K est un sous-corps de L appelé fermeture algébrique de K dans L.
-
- Soit K un corps, il existe un corps L, extension algébrique de K, tel que tout polynôme irréductible de L est de degré 1. L est appelé la clôture algébrique de K.
Les extensions algébriques L possèdent quelques propriétés élémentaires:
- Si L est de dimension finie notée [L:K] alors L est une extension algébrique de K.
- Si L est une extension finie de K de dimension finie [L:K] et si K est une extension finie de H, alors L est une extension finie de H de dimension [L:K].[K:H].
-
- L dispose d'une structure d'espace vectoriel sur K.
Pour s'en assurer, il suffit de vérifier que les axiomes définissant un espace vectoriel sont bien vérifiés pour L. La démonstration est alors évidente.
-
- Si L est de dimension finie notée [L:K] alors L est une extension algébrique de K.
Considérons l un élément de L et n un entier positif égal à [L:K]. Alors la famille (1, l, l2,...,ln) est liée car elle contient plus d'éléments que la dimension de l'espace. Il existe donc une combinaison linéaire nulle de cette famille et dont les coefficients ne sont pas tous réduits à 0. Cette combinaison linaire définit un polynôme non nul qui possède l pour racine, ce qui montre son caractère algèbrique.
-
- Si L est une extention de K de dimension finie [L:K] et si K est une extention de H de dimension finie [K:H], alors L est une extension de H de dimension [L:K].[K:H].
Soit (h1, h2, ..., hn) une base de KH(respectivement (l1, l2, ..., lm) une base de LK). Il est aisé de vérifier que la famille (hi.lj) est une base de LH, ce qui démontre la proposition.
Extension algébrique et polynôme
Article détaillé Corps de rupture
Soit K un corps et P[X] un polynôme à coefficient dans K. Alors il existe une extension algébrique de K contenant au moins une racine de P[X]. Cette extension est appelée corps de rupture. Dans le cas où le polynôme est irréductible de degré n alors le corps de rupture possède une dimension, en tant qu'espace vectoriel sur K égale à n.
- Soit P[X] un polynôme sur K, alors il existe une extension finie L' de K tel que le polynôme P[X] admet toutes ses racines dans L' . On dit alors que le polynôme est scindé dans L' .
-
- Soit P[X] un polynôme sur K, alors il existe une extension finie L' de K tel que le polynôme P[X] admet toutes ses racines dans L' .
Le polynôme P[X] est le produit d'un polynôme scindé et de polynômes irréductibles de degré supérieur ou égal à 2.
![P[X]=S[X]\prod_{i=1}^n Q_i[X]](https://static.techno-science.net/illustration/Definitions/autres/b/bfe4e5df5aa52d689b614d2da26c1111_9915000d11f075ed1c1a146387377e91.png)
Si n est égal à 0, c’est-à-dire si le polynôme P[X] est scindé, alors K est donc l'extension recherchée. Dans le cas contraire, démontrons la proposition par récurrence sur le degré p du polynôme produit des polynômes irréductibles.
Si p est égal à 2, ce qui est la plus petite valeur possible par construction, alors n est égal à 1 et la proposition précédente montre l'existence d'un corps L tel que Q1[X] admette une racine. Ce polynôme est alors scindé car il est de degré 2. L est donc l'extension recherchée.
Supposons la propriété vraie pour toute valeur inférieure ou égal à p. Supposons alors que le produit des polynômes irréductibles soit de degré p+1. Il existe alors une extension K1 tel que le polynôme Q1[X] admette au moins une racine. Sur K1le polynôme Q1[X] est alors produit S'[X].Q'1 d'un polynôme scindé et d'un polynôme de degré strictement inférieur à celui de Q1[X]. Par hypothèse de récurrence il existe une extension finie L de K1 minimale tel que le polynôme P[X] est scindé sur L. L est de dimension [K1:K].[L.K1] sur K. C'est donc une extension finie, elle est donc algèbrique.
Extension algébrique et sur-corps
Si l'on considère un polynôme à coefficients rationnels, alors le paragraphe précédent montre qu'il est possible de construire des extensions de


![\mathbb{Q}[X]/P[X]](https://static.techno-science.net/illustration/Definitions/autres/b/b7daf9f332b682a82e4f242210a06053_92f1257cddc877c1a66877780d24da51.png)


- Soit P[X] un polynôme irréductible de degré n sur K, L une extension finie de dimension n sur K contenant une racine du polynôme et F une extension contenant au moins une racine de P[X]. Alors F est une extension de L.
- Soit P[X] un polynôme sur K, alors il existe une extension finie minimal L' de K tel que le polynôme P[X] admet toutes ses racines dans L' . Minimal signifie ici que toute extension F contenant toutes les racines de P[X] est une extension de L. Cette extension est appelée corps de décomposition de P[X].
Cette analyse des sur-corps permet de démontrer les propositions suivantes:
- Si L est une extension algébrique d'un corps K et si (a1, a2, ..., an) est une famille de L, alors il existe un plus petit sous-corps de L contenant la famille, et ce sous-corps est une extension finie de K. On note ce sous-corps K(a1, a2, ..., an).
- Si K est une extension algébrique d'un corps H et si L est une extension algébrique de K, alors L est une extension algébrique de H.
Soit L une extension finie de K. Soit l un élément de L. On appelle polynôme minimal de l le polynôme unitaire (c’est-à-dire dont le monôme dominant a pour coefficient 1) qui engendre l'idéal annulateur c’est-à-dire l'idéal des polynômes qui possède l pour racine. C'est le polynôme de plus petit degré qui possède l pour racine.
- Le degré du polynôme minimal de l divise [L:K].
-
- Soit P[X] un polynôme irréductible de degré n sur K, L une extension finie de dimension n sur K contenant une racine du polynôme et L' une extension contenant au moins une racine de P[X]. Alors L' est une extension de L.
Soit β une racine de P[X] dans L' . Considérons alors l'application j de L dans L' définie par :
![\forall x \in L \;et\; (x_i)_{i \in [0, n-1]}\in K^n \quad x=\sum_{i=0}^{n-1}x_i \alpha^i \Rightarrow j(x)=\sum_{i=0}^{n-1}x_i \beta^i](https://static.techno-science.net/illustration/Definitions/autres/e/e0654ca2a7da0930e63a3c73289e533b_753f606adb149264d450e299f5281cea.png)
L'application j est un morphisme d'espace vectoriel, il suffit donc de démontrer qu'elle est aussi un morphisme pour la multiplication interne. Soit a et b deux éléments de L, alors il existe deux polynômes A[X] et B[X] tel que a = A(α) et b = B(α). Les égalités suivantes montrent que j est aussi un morphisme pour l'addition.
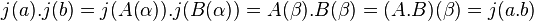
Ce qui termine la démonstration.
-
- Soit P[X] un polynôme sur K, alors il existe une extension finie minimal L' de K tel que le polynôme P[X] admet toutes ses racines dans L' . Minimal signifie ici que toute extension F contenant toutes les racines de P[X] est une extension de L.
Le polynôme P[X] est le produit d'un polynôme scindé et de polynômes irréductibles de degré supérieur ou égal à 2.
![P[X]=S[X]\prod_{i=1}^n Q_i[X]](https://static.techno-science.net/illustration/Definitions/autres/b/bfe4e5df5aa52d689b614d2da26c1111_9915000d11f075ed1c1a146387377e91.png)
Si n est égal à 0, c’est-à-dire si le polynôme P[X] est scindé, alors K est l'extension minimale tel que le polynôme soit scindé. Dans le cas contraire, démontrons la proposition par récurrence sur le degré p du polynôme produit des polynômes irréductibles.
Si p est égal à 2, ce qui est la plus petite valeur possible par construction, alors n est égal à 1 et la proposition précédente montre l'existence d'un corps L tel que Q1[X] admette une racine. Ce polynôme est alors scindé car il est de degré 2. La première proposition montre que F est une extension de L.
Supposons la propriété vraie pour toute valeur inférieure ou égal à p. Supposons alors que le produit des polynômes irréductibles soit de degré p+1. Il existe alors une extension K1 tel que le polynôme Q1[X] admette au moins une racine. Sur K1le polynôme Q1[X] est alors produit S'[X].Q'1 d'un polynôme scindé et d'un polynôme de degré strictement inférieur à celui de Q1[X]. Par hypothèse de récurrence il existe une extension finie L de K1 minimale tel que le polynôme P[X] est scindé sur L. L est de dimension [K1:K].[L.K1] sur K.
Montrons enfin que F est une extension de L. F est une extension de K1 qui contient toutes les racines du polynôme produit de S[X], S'[X], Q'1 et des Qi. Par hypothèse de récurrence, c'est donc une extension de L. Et la proposition est démontrée.
- Si L est une extension algébrique d'un corps K et si (a1, a2, ..., an) est une famille de L, alors il existe un plus petit sous-corps de L contenant la famille, et ce sous-corps est une extension finie de K.
Soit Pi>/sub>[X] le polynôme minimal de ai à coefficiant dans K. Ce polynôme existe car ai est algèbrique sur K. Le propduit de tous ces polynômes admet pour racines tous les éléments de la famille. L'idéal annulateur de cette famille dans K[X] est donc non vide. Soit P[X] le polynôme générateur de cet idéal. Il existe un sous-corps de L isomorphe au corps de décomposition de P[X]. D'après la proposition précédente, ce sous-corps est de dimension finie et est le plus petit contenant la famille, et la proposition est démontrée.
-
- Si K est une extention algébrique d'un corps H et si L est une extention algébrique de K, alors L est une extention algébrique de H.
Soit l un élément de L. Il existe un polynôme à coefficients dans K annulant l car L est algèbrique sur K. Notons (a1, a2, ..., an) la famille des coefficiants du polynôme, notons F le corps H(a1, a2, ..., an) F est de dimension finie sur H, F(l) est de dimension finie sur F et l est inclu dans F(l) qui est de dimension [F(l):F].[F:H] sur H. Et donc, l est inclu dans une extension de dimension finie de H ce qui démontre la proposition.
-
- Le degré du polynôme minimal de l divise [L:K].
Considérons la plus petite extension K1 de K contenant l. Sa dimension est égale au degré du polynôme minimal n de l. Or L est aussi une extension de K1. L'égalité suivante démontre alors le résultat: [L:K] = n.[K1:K]
Extensions particulières
Extension quadratique
article détaillé: Extension quadratique
Les extensions quadratiques interviennent notamment pour la résolution des problèmes de l'antiquité sur les nombre constructibles. Ces nombres forment un corps inclu dans les nombres réels et stable par la fonction racine carrée, c’est-à-dire que la racine carré d'un nombre constructible positif est aussi constructible. Une identification du plan euclidien et des nombres complexes montre que les nombres constructibles forme le plus petit corps contenant i le nombre imaginaire pure, les nombres rationnels et stable par la fonction conjugée et la fonction racine carrée.
Un tel corps peut se construire à l'aide d'une suite infinie d'extensions quadratiques des nombres rationnels (K0, K1, ... , Kn, ...) où K0 est le corps des nombres rationnels et Kn est une extension quadratique du corps Kn-1 si n est strictement positif. Tout nombre constructible s'obtient comme élément d'un corps construit à partir d'une suite finie de corps construits comme extension quadratique du corps précédent dans la suite. On parle alors de tour d'extensions quadratiques.
Une fois cette propriété démontrée, il devient aisé de résoudre les problèmes de l'antiquité comme la duplication du cube. En effet, la duplication du cube demande de construire un nombre d dont le polynôme minimal est de degré trois. Or la dimension de toute extension contenant d est du type 2p ou p est un entier. Comme le degré du polynôme minimal d'un élément d'une extension algébrique divise toujours la dimension de l'extension algébrique, le problème n'a pas de solution.
Une approche analogue montre l'impossibilité de la résolution dans le cas général de la Trisection de l'angle par les méthodes de la rêgle et du compas et permet de déterminer les polygones réguliers constructibles.
Extension de Galois
Article détaillé : Extension de Galois
Un autre outil est essentiel pour l'analyse des extensions L d'un corps K, il correspond aux automorphismes de L laissant le corps K invariant. L'ensemble des automorphismes munis de la loi de composition interne des fonctions forme une structure de groupe. Cet outil est particulièrement efficace dans le cas des extensions finies par exemple sur le corps des rationnels dans le cas d'un corps de décomposition. Un élément de ce groupe restreint à un ensemble de racines d'un polynôme correspond à une permutation de cet ensemble de racines. Dans le cas des extensions finies, il correspond à un groupe fini appelé Groupe de Galois.
Pour que cet outil soit pleinement pertinent, il faut en fait que les polynômes minimaux de l'extension n'aient pas de racines multiples. Ce qui est le toujours le cas pour des extensions sur les corps des rationnels ou pour les extensions dans le cas d'un corps de caractéristique nulle. Dans ce cadre, il est par exemple possible de montrer qu'il existe un élément a dit primitif tel que l'extension soit une extension simple égal à K(a). Il faut de plus que l'extension contienne suffisamment de racines. Il faut en fait que le cardinal du groupe soit égal à la dimension de l'extension. Si ces deux hypothèses sont vérifiées, on parle alors d'extension de Galois.
Le groupe de Galois permet de comprendre finement la structure de l'extension. Par exemple, il existe une bijection entre ses sous-groupes et les sous-corps de l'extension. Il est utilisé pour la détermination des polygones constructibles à la rêgle et au compas ou pour le théorème d'Abel sur la résolution d'équations polynomiales par radicaux.
Clôture algébrique
Article détaillé : Clôture algébrique
Il existe une extension algébrique particulière, celle qui ne possède pour polynôme minimaux que les polynômes de degré 1. C'est l'extension pour lequel tous les polynômes de degré différent de zéro admettent au moins une racine. Dans le cas des nombres réels, l'extension finie décrite plus haut suffit pour obtenir une clôture algébrique. Dans le cas des nombres rationnels, la clôture algébrique s'obtient soit par l'ensemble des nombres algèbriques des nombres complexes (on vérifie aisément que cet ensemble forme un corps) soit comme union dénombrable d'une suite croissante d'extensions. Si la clôture algébrique des nombres réels est un espace de dimension deux sur les réels, en revanche l'extension algébrique des nombres rationnels est de dimension infinie. Il suffit pour s'en convaincre de remarquer que pour tout entier, il existe un polynôme minimal de degré strictement supérieur à cet entier, la dimension est donc supérieure à tout entier. La preuve de la clôture algébrique du corps des nombres complexes est donnée par le théorème de d'Alembert-Gauss, il n'existe aucune preuve connue purement algébrique, l'utilisation d'outils topologiques est jusqu'à maintenant toujours nécessaire.
Dans le cas général, tout corps possède comme une extension la clôture algébrique. Néanmoins, la preuve de ce théorème nécessite généralement d'admettre l'axiome du choix. Elle est en effet souvent obtenue par une suite infinie d'extensions algébriques emboîtées.
Il n'existe aucun corps fini algébriquement clos. En effet, le produit ∏ (Xi - ai ) + 1 est un polynôme irreductible si les ai parcourent l'ensemble du corps.
Enfin, soit une extension finie L d'un corps K, elle est alors isomorphe à un sous-corps de la clôture algébrique Ω de K. Pour s'en convaincre, il suffit de considérer une suite (l1, l2, ... ,ln)d'éléments générateurs de L. Une récurrence sur le nombre d'éléments de la suite permet de conclure. Si elle ne contient qu'un élément l1 soit P1[X] le polynôme minimal de l1 dans K. Soit λ1 une racine de P1[X] dans Ω, alors K(l1) dans L est isomorphe à K(λ1) dans Ω. Dans le cas général, K(l2, ... ,ln) est une extension de K(λ1) générée par n-1 éléments, la récurrence permet de conclure.

















































