Arithmétique modulaire - Définition

Cryptographie

L'hameçonnage est une technique visant à obtenir des informations confidentielles sur internet en vue d'une escroquerie. La nécessité de communication d'informations confidentielles représente un danger en cryptographie.

L'objet de la cryptographie est d'assurer sécurité dans la transmission des messages. La confidentialité ainsi que l'authentification de ceux-ci sont deux exemples du sens donné au terme sécurité. On peut citer deux exemples : la protection des messages qu'utilise une armée pour empêcher une anticipation de l'ennemi, ou la carte bleue proposée par le système bancaire, offrant à un usager une bonne sécurité.

En termes plus mathématiques, l'opération de chiffrement se traduit par un algorithme, c'est-à-dire une fonction f qui, à un message en clair m et une clé k, associe un message chiffré f(k, m). La connaissance du message chiffré et de l'algorithme doit être insuffisante pour reconstituer le message en clair sans une clé de déchiffrement. Dans le cas de la cryptographie traditionnelle, dite cryptographie symétrique, la clé de déchiffrement est identique à la clé de chiffrement ou s'en déduit aisément. Cette clé doit alors rester secrète.

La cryptographie asymétrique s'appuie sur le constat que seule la clé de déchiffrement doit rester secrète, et connue du seul récepteur du message. Elle n'a pas besoin d'être communiquée à ses correspondants. Alice utilise la clé de chiffrement de Bob, que celui-ci a rendu publique, pour lui envoyer un message. Seul Bob peut le déchiffrer, même Alice, si jamais elle avait perdu le message en clair, en serait incapable. Bob doit répondre en utilisant la clé de chiffrement d'Alice.

L'objectif est donc de définir une fonction simple à évaluer mais difficile à inverser sans la connaissance d'un secret. L'arithmétique modulaire a été la première à offrir des solutions, et elle est toujours à la base de beaucoup de solutions commerciales. Par exemple l'échange de clés Diffie-Hellman, premier exemple historique, exploite la difficulté pratique à inverser l'exponentiation modulaire. Cette dernière, ou ses généralisations à d'autres groupes, reste fondamentale dans le domaine.

La cryptographie asymétrique résout en particulier le délicat problème de la distribution des clés en cryptographie symétrique. Si plusieurs correspondants communiquent, en cryptographie symétrique, une clé différente s'avère nécessaire pour chaque couple d'intervenants, alors qu'en cryptographie asymétrique chaque correspondant dispose d'une clef qu'il garde secrète, et d'une clef qu'il rend publique. Cependant elle n'a pas fait disparaître les codes symétriques, qui offrent des algorithmes beaucoup plus efficaces. Pour une sécurité équivalente, les codes symétriques présentent l'avantage de nécessiter des clés nettement plus petites, 128 bits pour la version courante de AES, contre plus d'un millier pour le RSA, mais surtout le chiffrement comme le déchiffrement sont de cent à mille fois plus rapide. Les systèmes cryptographiques modernes, comme ceux utilisés par les cartes bancaires, ou le protocole de communication cryptée SSL/TLS très utilisé sur Internet, n'utilisent qu'en début de communication la cryptographie asymétrique, pour échanger les clés d'un chiffrement symétrique qui prendra ensuite le relais.

Cryptographie asymétrique

Le code RSA est un exemple largement répandu de cryptographie asymétrique. Il se décrit de la manière suivante :

Alice (le choix des prénoms est traditionnel) souhaite pouvoir recevoir des messages de Bob sans qu'Ève puisse les déchiffrer. Alice choisit deux grands nombres premiers p et q et un entier e, premier avec l'ordre g du groupe des unités de Z/pqZ. Ici g est égal à (p - 1)(q - 1), soit la valeur de la fonction indicatrice d'Euler en n=pq. Les messages sont supposés être des éléments de cet anneau. Si Bob souhaite transmettre le message m à Alice, il transmet la valeur de m^e modulo n. Alice a rendu au préalable publiques les valeurs de n = pq, e et donc la fonction f de chiffrement, qui est ici égale à :

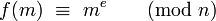
Ève a pu intercepter la connaissance de f, e et n, ces informations sont en effet publiques. En revanche, elle ne peut intercepter les valeurs de p et q qui n'ont jamais été communiquées.

Pour Bob, la fonction de codage est aisée : il s'agit d'une simple exponentiation modulaire. Pour Alice la lecture l'est aussi, il lui suffit de trouver une solution à l'identité de Bézout :

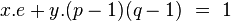
Si (x₀, y₀) est une solution, alors le théorème d'Euler montre que :

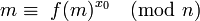
En revanche Ève ne connaît pas a priori la décomposition en produit de facteurs premiers de n. Elle doit calculer le logarithme discret de f(m), ce qui constitue un problème ardu. La méthode la moins lente connue correspond à déterminer les valeurs de p et de q. Si n est grand, il n'existe pas, à l'ordre du jour, d'algorithme assez efficace pour résoudre cette question.

La clé permettant le chiffrement est la donnée de e et n. La force d'un tel système réside dans le fait que la connaissance de cette clé ne permet pas le décryptage, elle peut donc être publique. Les valeurs de p et q constituent la clé de déchiffrement.

Cryptographie symétrique

La cryptographie asymétrique n'existerait pas sans les méthodes issues de l'arithmétique modulaire. Celle-ci ne joue pas le même rôle fondateur en cryptographie symétrique, mais n'en est pas absente pour autant. Les chiffrements symétriques se divisent en deux grandes familles dont l'une, les chiffrements par flot, utilise souvent comme composant de base les suites récurrentes linéaires sur un corps fini (voir ci-dessous) ; l'autre, celle des chiffrements par bloc, comprend entre autres le DES et son successeur, le standard de chiffrement avancé, appelé couramment AES (pour Advanced Encryption Standard). Ces derniers opèrent sur des blocs de données d'une taille fixe comptée en octets, huit pour le DES par exemple. Une suite d'opérations primitives assez simples est appliquée de façon répétée pour coder un bloc. Un octet, ou plus généralement un bloc de n bits, peut être vu comme les coefficients d'un polynôme sur les entiers modulo deux, de degré maximal n-1. Cela a conduit les cryptologues à s'intéresser à certaines opérations sur les corps finis de caractéristique 2. Ainsi il s'avère que l'opération d'inversion sur le corps fini F_2ⁿ, composée avec une transformation affine, a de bonnes propriétés cryptographiques pour en faire l'une des primitives des chiffrements par bloc. Ceci a été exploité par les auteurs du chiffrement Rijndael, qui est devenu l'AES. La publication officielle de ce dernier par le NIST (agence fédérale américaine) contient d'ailleurs quelques préliminaires mathématiques sur le sujet. Cependant il n'est nul besoin d'algorithmique sur l'arithmétique ou les corps finis pour l'implémentation : ces opérations sont représentées par des tables, comme les opérations analogues du DES obtenues elles de façon beaucoup plus heuristique. Certains cryptologues ont vu une faiblesse potentielle dans la caractérisation trop algébrique de Rijndael, qui le rendrait plus accessible à l'imagination des mathématiciens, ce qui n'a pas empêché son adoption pour l'AES.

Test de primalité

Les codes RSA utilisent comme clés les nombres premiers p et q du paragraphe précédent. L'usage, pour les trouver, consiste à choisir un nombre presque au hasard, de tester s'il est premier ou non et de recommencer s'il ne l'est pas.

Le crible d'Ératosthène est une méthode rapide pour les petits nombres. Utilisé habilement, 46 tests suffisent pour vérifier la primalité d'un nombre inférieur à 39000. En revanche, il est inefficace pour une application industrielle employant des nombres qui s'écrivent avec plusieurs centaines de chiffres.

La majorité des tests de l'industrie se fondent sur des variantes du petit théorème de Fermat. Si un nombre p est premier, alors pour tout entier a, a^p est congru à a modulo p. La réciproque est fausse : il existe des nombres non premiers, appelés nombres de Carmichaël (par exemple 561 = 3 · 11 · 17), pour lesquels la congruence est vraie pour toute valeur de a. Toutefois, si p n'est ni un nombre de Carmichaël, ni un nombre premier, la congruence est fausse pour au moins la moitié des valeurs de a comprises entre un et p. Que la congruence soit vérifiée pour un grand nombre de valeurs de a indique une très forte probabilité de primalité pour p, s'il n'est pas un nombre de Carmichaël.

Le test de primalité de Solovay-Strassen et surtout le test de primalité de Miller-Rabin sont deux exemples largement utilisés. Ils se fondent sur une analyse plus poussée du petit théorème de Fermat et n'admettent pas d'analogues aux nombres de Carmichaël, ce qui lève l'un des problèmes du test de Fermat. Pour ces deux méthodes, un test de primalité déterministe consiste à vérifier la propriété pour un nombre de valeurs de a garantissant une preuve irréfutable. Le nombre de calculs à effectuer étant rédhibitoire, on se contente d'un test probabiliste. Il consiste à vérifier la congruence sur un ensemble de valeurs de a, choisi pour assurer une probabilité de primalité supérieure à une valeur donnée, souvent égale à 1 - (1/2)¹⁰⁰.

Décomposition en produit de facteurs premiers

La sécurité par l'obscurité n'est pas de mise pour les codes RSA. Il est important de connaître précisément l'état de l'art de la décomposition des entiers en termes de facteurs premiers. Un concours appelé compétition de factorisation RSA fut ouvert jusqu'en mai 2007, proposant un prix pour quiconque capable de factoriser un nombre choisi dans une liste rendue publique.

Le crible d'Ératosthène est un test de primalité qui offre une méthode de décomposition. Mais une fois encore, il n'est pas applicable pour de grands nombres car trop lent.

Les différentes méthodes actuellement utilisées reposent souvent sur les résidus quadratiques. Un diviseur de zéro est un résidu quadratique contenant comme représentants au moins deux carrés parfaits. L'objectif est de trouver ces deux carrés. Cette approche est celle du crible quadratique et de l'algorithme de factorisation par crible sur les corps de nombres généralisé, le plus rapide connu en 2007. On peut encore citer l'algorithme ρ de Pollard qui utilise le paradoxe des anniversaires.

Corps fini

De même que pour l'arithmétique des mathématiques pures, d'autres structures sont nécessaires pour exploiter les capacités offertes par l'arithmétique modulaire. En informatique, les nombres sont codés sur n bits, c'est-à-dire correspondent à une suite de longueur n composée de zéros et de uns. Une telle suite peut être considérée comme un vecteur d'un espace vectoriel de dimension n sur le corps fini F₂ à deux éléments.

Cette structure est souvent considérée comme l'espace des polynômes à coefficients dans F₂. Pour garantir la stabilité de la multiplication, la logique de Gauss est appliquée, cet espace est quotienté par un polynôme irréductible (l'équivalent d'un nombre premier) de degré n. La structure obtenue est le corps fini de cardinal 2ⁿ. Un nombre a modulo 2ⁿ et un polynôme P[X] du système modulaire sont très semblables, ils s'écrivent en effet :

Un exemple d'utilisation est la création d'un générateur de nombres pseudo-aléatoires dans F₂. De tels générateurs sont utilisés par exemple pour le chiffrement de flux A5/1 utilisé dans le contexte d'une communication orale par téléphone portable. Un élément de l'algorithme est la constitution d'un registre à décalage. Étant données deux suites finies d'éléments de F₂ de longueur n, une suite de coefficients et une séquence d'initialisation, soient :

   et   

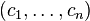
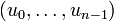
un tel registre fournit une suite pseudo-aléatoire (u_j), obtenue par récurrence linéaire :

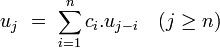
La suite des coefficients est souvent fixe. La clé est alors la séquence d'initialisation, qui peut être représentée par un entier a modulo 2ⁿ :

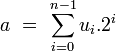
La suite obtenue est périodique, cependant si la suite des coefficients est bien choisie, la période est très longue : 2n - 1. Cette situation se produit si le polynôme de rétroaction R[X], donnée par la formule suivante, est le polynôme minimal d'un élément primitif du groupe cyclique F2n*.

Analyse harmonique sur un groupe abélien fini

Les idées de Dirichlet s'appliquent sur le système modulaire du paragraphe précédent. Pour l'addition, l'espace vectoriel V précédent est un groupe abélien fini. Les caractères de ce groupe forment une base orthonormale de l'ensemble des fonctions de V dans celui des nombres complexes. Il est à noter que l'ensemble d'arrivée choisi n'est pas toujours celui des complexes mais parfois le corps F₂. Les résultats sont strictement identiques. Une telle structure dispose d'une analyse harmonique. Si l'ensemble d'arrivée est choisi égal à F₂ la transformée de Fourier prend le nom de transformée de Walsh. Cette approche est utilisée à la fois pour les systèmes DES, RSA et certains chiffrements de flux.

Un registre à décalage est trop aisément déchiffrable. Pour un registre de longueur n, même si la suite engendrée est de période 2ⁿ - 1, l'algorithme de Berlekamp-Massey permet de déterminer celle-ci grâce la connaissance de 2n valeurs consécutives, avec une complexité quadratique. Ainsi, si la clé est composée de 128 bits, il suffit de 128 x 128 · k = 16 384 · k étapes pour le décrypter, où k est suffisamment « petit » pour que cela représente une sécurité insuffisante. La solution adoptée consiste à utiliser plusieurs registres à décalage. Les différents résultats sont vus comme un élément d'un nouvel espace vectoriel sur F₂. Une fonction booléenne associe à chaque élément de cet espace la valeur un ou zéro. Si une telle fonction est bien choisie, le meilleur algorithme de déchiffrement connu demande de l'ordre de 2ⁿ étapes pour trouver le signal apportant la confusion. La détermination de cette fonction est obtenue à l'aide des outils de l'analyse harmonique.

Pour un code RSA et à la fin du XX^e siècle, la clé est souvent un nombre dépassant 10³⁰⁸. Il est important de disposer d'une multiplication rapide sur les grands moduli. La technique consiste à identifier les moduli aux polynômes sur un corps fini. La multiplication de deux polynômes de degré n est une opération qui, si elle est réalisée de manière naïve, impose une complexité quadratique. Les caractères du groupe additif associés étant orthogonaux, la complexité devient linéaire si une telle base est utilisée. Un calcul plus rapide consiste à réaliser une transformée de Fourier rapide, à multiplier les deux résultats et à opérer la transformée de Fourier inverse. La complexité totale est alors en n log(n) où log désigne ici le logarithme de base deux.