Mathématiques en Europe au XVIIe siècle - Définition

Des outils théoriques qui s'affinent

C'est au cours de ce siècle que se mettent en place des outils nécessaires au développement des mathématiques principalement en analyse.

Algèbre

La révolution symbolique initiée par François Viète de 1591 à 1603 se poursuit avec la publication de ses oeuvres par Alexander Anderson (1612-1619), Marin Ghetaldi (1615), Jean-Louis Vaulezard (1630), Claude Hardy (1630), Jean de Beaugrand (1624 et 1631), James Hume (1636) et Frans Van Schooten (1646). Cette nouvelle algèbre (on préfère alors le terme d'analyse symbolique) est amplifiée par les travaux des anglais Nathanael Tarporley, William Oughtred et Thomas Harriot et du français Pierre de Fermat. Ainsi, se mettent en placent toutes les règles du calcul littéral. Sa mise en forme définitive s'achève avec Descartes dans ses Regulae et dans sa Géométrie (1637), qui, outre les opérations usuelles (additions, multiplication, soustraction, division, racine carré et racine cubique), fournit une définition de l'exponentielle. Cette période de formation du calcul algébrique (1591-1637) voit se réaliser une véritable rupture avec les rédactions plus anciennes. Elle va permettre une plus grande lisibilité dans la résolution des équations, le traitement des polynômes et la mathématisation des problèmes.

Gottfried Wilhelm Leibniz.

S'appuyant sur les travaux de ses prédécesseurs, Leibniz approfondit l'usage de la notation symbolique dans des ouvrages marquants comme Conspectus calculi et Mathesis universalis. Il exploite à son avantage cet outil pour développer de nouvelles méthodes de résolution dans son De arte combinatoria (1666). Il s'attache à la résolution des systèmes d'équations linéaires et met en place pour la première fois la notion de déterminant (1684), celle d'élimination et de résultante. Il applique son imagination à cette nouvelle écriture pour créer du neuf et invente le concept de puissance réelle d'un réel avant de pouvoir en donner une définition mathématique rigoureuse. Il est suivi ou précédé dans cette recherche par Isaac Newton.

Arithmétique

L'arithmétique apparait en Europe durant ce siècle. Les mathématiciens redécouvrent le savoir de l'antiquité et développent de nouvelles techniques pour résoudre des questions parfois anciennes. Ils se limitent à la branche des mathématiques appelée arithmétique modulaire.

Bachet de Méziriac traduit le livre de Diophante d'Alexandrie Arithmetica en latin et il démontre l'identité maintenant connue sous le nom d'identité de Bézout. Ce sujet passionne Pierre de Fermat qui énonce un grand nombre de propositions sur ce sujet. On peut citer son petit théorème, celui sur les deux carrés et son dernier théorème. La communauté scientifique se lance des défis sur ce sujet, ainsi Fermat demande : « un nombre carré qui, ajouté à la somme de ses parties aliquotes (ie ses diviseurs), fasse un cube. » Il conclut par : « j'attends la solution de ces questions ; si elle n'est fournie ni par l'Angleterre, ni par la Gaule Belgique ou Celtique, elle le sera par la Narbonnaise ».

Les nombres premiers fascinent. Mersenne en développe une famille et Fermat une autre. Ils communiquent largement entre eux sur ce sujet, comme l'atteste cette lettre de Fermat : « Si je puis une fois tenir la raison fondamentale que 3, 5, 7, 17, 257, 65 537, ..., sont nombres premiers, il me semble que je trouverai de très belles choses en cette matière, car j'ai déjà trouvé des choses merveilleuses dont je vous ferai part ». René Descartes n'est pas en reste. Il cherche en vain à démontrer que si la division par huit d'un nombre premier donne pour reste un ou trois, il s'écrit de la forme x² + 2y².

On peut encore citer Leibniz qui démontre un résultat redécouvert au XVII^e siècle et qui prendra le nom de théorème de Wilson. Il propose aussi une démonstration plus rapide vers 1683 du petit théorème de Fermat.

Géométrie

Durant ce siècle, la géométrie se détache de la notion ancienne d'ensemble de points ou de figures de référence pour entrer dans l'ère de la géométrie des coordonnées créée par Pierre de Fermat et René Descartes. Ces mathématiciens cherchent à associer des courbes et des surfaces à des équations algébriques et permettent ainsi un échange fructueux entre deux domaines (géométrie et algèbre). Descartes met en place les outils de calcul de tangente au point A à une courbe en recherchant la droite passant par A et ne possédant en commun avec la courbe qu'un point double. De même, la méthode des cercles tangents lui permet de trouver de manière algébrique la normale à la courbe (la perpendiculaire à la tangente). Il définit les courbes géométriques à l’aide de mouvements à condition « qu’ils soient bien réglés entre eux », et donne une méthode universelle, avec introduction d’un élément d’unité, de la géométrie algébrique. Parallèlement, Fermat s'attache à l'étude des maxima et des minima.

En réaction contre cette tendance de la géométrie traitée par les nombres dans ce qui devient la Géométrie Analytique, Leibniz développe l'idée qu'il doit être possible de trouver pour la géométrie des outils aussi performants qu'ont été les notations de Viète pour l'Algèbre. C'est son projet d'Analysis Situs qu'il ne réussira jamais à mettre au point.

Desargues, quant à lui, dans son ouvrage paru en 1636, Pratique de la perspective développe une approche projective de la géométrie et complète son étude trois ans plus tard par l'exploration des coniques. Son travail est repris et approfondi par Blaise Pascal, Philippe de La Hire et Isaac Newton (Philosophiae naturalis principia mathématica 1687).

Analyse

John Wallis

Portrait d'Isaac Newton par Godfrey Kneller (1689).

C'est surtout dans ce domaine que l'on note un progrès considérable avec la notion de limite et de calcul infinitésimal. La construction des tangentes aux courbes étudiée par Descartes, Fermat et Roberval pose les premiers jalons du calcul différentiel. Dès le début de ce siècle se pose la question de la recherche de l'inverse des tangentes (ou comment trouver une courbe quand on connaît une propriété tangentielle). En 1645, Roberval propose ses quadratrices.

Le début du XVII^e voit le développement de l'étude des aires sous les courbes ; Cavalieri met en place sa méthode des indivisibles (Geometria indivisibilibus continuorum nova quadam ratione promata, 1635) développée par Torricelli, Stefano degli Angeli, Gregory et Wallis.

Sa méthode, novatrice, est cependant supplantée à la fin du XVII^e siècle quand se met en place le calcul infinitésimal et intégral développé conjointement par Leibniz (les infiniment petits, Nouveau calcul, 1684) et Newton (les fluxions, écrit en 1670 et publié en 1690). Dès la parution du calcul différentiel de Leibniz, sa méthode est utilisée dans le monde des mathématiciens. John Craig l'exploite dans un livre traitant des quadratures. Leibniz comprend que sa méthode permet de résoudre le problème inverse des tangentes (l'intégration) et c'est Jacques Bernoulli qui emploie pour la première en 1690 le terme intégral. Jacques et Jean Bernoulli utilisent ce nouveau calcul pour l'étude de courbes particulière (courbe isochrone, courbe brachistochrone). En 1696, le marquis de l'Hospital, instruit par Jean Bernouilli, publie Analyse des infiniment petits pour l'intelligence des lignes courbes. Ce nouveau calcul présente des imprécisions qui seront levées à la fin du siècle et au début du siècle suivant grâce à un grand débat ouvert à l'Académie Royale des Sciences. Le calcul des fluxions de Newton trouve, quant à lui, un développement parmi les mathématiciens anglais.

Dans la seconde moitié du XVII^e siècle, l'école anglaise est florissante. John Wallis approfondit le calcul des indivisibles. Avec James Gregory et Isaac Newton, il travaille sur le développement en série entière. Mercator découvre l'aire sous l'hyperbole en développant en série 1/(1+x) (Logarithmotechnia, 1668). Isaac Newton développe en série Arccos, Arcsin, cos et sin (avant 1670).

Le XVII^e siècle voit aussi la naissance de deux fonctions transcendantes : la fonction logarithme et la fonction exponentielle . Mise en place par John Napier (1614) qui lui donne le nom de logarithme (logarithme d'un sinus), et Jost Bürgi (1620), La fonction logarithme n'est au départ qu'une table de correspondances pour des calculs astronomiques. Henry Briggs en 1615 propose une table de logarithmes décimaux. Puis c'est l'invention de la règle à calcul en 1624 par Edmund Gunter. De tables de correspondances, le logarithme prend progressivement le statut de fonction avec l'aire sous l'hyperbole attribuée à Grégoire de Saint-Vincent (1647), étudiée aussi par James Gregory (1667) et Huygens qui font le lien entre cette aire et les propriétés des logarithmes. En 1668, Brouncker et Mercator les développent en série entière (log 2, log 5/4, puis log (1+x)) puis vient sa définition intégrale écrite par Leibniz sous la forme . La fonction exponentielle n'est au départ que l'extension de aⁿ à des exposants d'abord négatifs puis fractionnaires. Elle s'appuie sur la notation exponentielle de Descartes (1637) développée ensuite par Leibniz mais c'est au cours du siècle suivant avec Euler que cette fonction sera complètement étudiée.

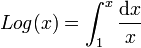
Tous ces nouveaux outils vont permettre le développement au siècle suivant de l'étude des fonctions et de la cinématique.