Mouvement à force centrale - Définition et Explications

quantité de mouvement coordonnées polaires mécanique quantique

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

En mécanique du point, un mouvement à force centrale est le mouvement d'un point matériel $M\,$ soumis uniquement à une force centrale, c'est-à-dire une force toujours dirigée vers le même point noté $O\,$ , appelé centre de force.

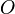
Ce type de mouvement est une modélisation de certains phénomènes physiques : il n'est pas rigoureusement présent dans la nature, mais certains mouvements s'en rapprochent. Par exemple, on peut considérer que la Terre (La Terre est la troisième planète du Système solaire par ordre de distance...) est soumise à une force (Le mot force peut désigner un pouvoir mécanique sur les choses, et aussi, métaphoriquement, un...) centrale de la part du Soleil (Le Soleil (Sol en latin, Helios ou Ήλιος en grec) est l'étoile...). Par ailleurs, lorsqu'on utilise une description classique de l'atome (Un atome (grec ancien ἄτομος [atomos], « que...), on peut considérer que le mouvement des électrons est à force centrale autour (Autour est le nom que la nomenclature aviaire en langue française (mise à jour) donne...) du noyau.

L'étude mathématique (Les mathématiques constituent un domaine de connaissances abstraites construites à l'aide...) de ce type de mouvements permet d'obtenir quelques résultats généraux. On peut montrer par exemple que la trajectoire (La trajectoire est la ligne décrite par n'importe quel point d'un objet en mouvement, et...) est contenue dans un plan, que la vitesse (On distingue :) aréolaire est constante, etc.

Historique

Galilée (Galilée ou Galileo Galilei (né à Pise le 15 février 1564 et mort à Arcetri près de Florence,...), dès 1610, pressent l'utilité de ce mouvement pour obtenir une histoire de la mesure du temps : après observation (L’observation est l’action de suivi attentif des phénomènes, sans volonté de les...) des satellites (Satellite peut faire référence à :) médicéens, il fait un appel d'offre en Europe (L’Europe est une région terrestre qui peut être considérée comme un...) pour le calcul des longitudes, mais celui-ci fut mal reçu. Cassini (La mission Cassini-Huygens est une mission spatiale automatique réalisée en collaboration par le...) I^er avec ses éphémérides de Io ne sera guère plus persuasif (voir Olaüs Roemer). Ensuite, le problème de l'établissement des cartes maritimes lança la Grande Concurrence, initiée par Galilée et Huygens (Horologium en 1653), entre horloge céleste et chronomètre de marine.

Le problème du mouvement à force centrale (En mécanique du point, un mouvement à force centrale est le mouvement d'un point...) fut résolut en premier par Isaac Newton (Isaac Newton (4 janvier 1643 G – 31 mars 1727 G, ou 25 décembre...) en 1687. Newton démontre en particulier que la trajectoire est contenue dans un plan passant par le centre de force et perpendiculaire (En géométrie plane, on dit que deux droites sont perpendiculaires quand elles se coupent en...) au moment cinétique (Le mot cinétique fait référence à la vitesse.), qui est alors constant. C'est d'ailleurs initialement dans le sens (SENS (Strategies for Engineered Negligible Senescence) est un projet scientifique qui a pour but...) inverse (En mathématiques, l'inverse d'un élément x d'un ensemble muni d'une loi de...) que Newton l'a démontré : le moment cinétique étant démontré constant, cela implique que la trajectoire est plane (La plane est un outil pour le travail du bois. Elle est composée d'une lame semblable à celle...). Cette trajectoire est décrite selon la seconde ( Seconde est le féminin de l'adjectif second, qui vient immédiatement après le premier ou qui...) loi de Kepler dite aussi lois des aires : des aires égales sont balayées dans des temps égaux.

Robert Hooke a résolu le cas particulier dit " de Hooke ", où la force centrale est proportionnelle à la distance séparant le centre de force du point (Graphie) en mouvement (voir ellipse de Hooke).

Jacques Binet exprima, au travers de ses formules, la vitesse et l'accélération (L'accélération désigne couramment une augmentation de la vitesse ; en physique,...) d'un point animé d'un mouvement à force centrale. Ces formules permettent, par exemple, d'obtenir les trajectoires elliptiques des planètes, redémontrant ainsi la première loi de Kepler.

Exemples

Quelques cas particuliers ont été étudiés mathématiquement :

le cas d'une force de rappel élastique : voir ellipse de Hooke (L'ellipse de Hooke est la trajectoire d'un mobile élastiquement lié à un point fixe.),
le cas des orbites bornées à énergie (Dans le sens commun l'énergie désigne tout ce qui permet d'effectuer un travail, fabriquer de la...) négative,
les cas des forces proportionnelles à $r p$ pour p valant -5, -3, 0, 1/3, 3/2, 5/3, 7/3, 5/2, 4, 5 ou 7.

Des exemples dans la nature ont également été traités :

le mouvement des planètes : voir lois de Kepler (En astronomie, les lois de Kepler décrivent les propriétés principales du mouvement...),
la diffusion (Dans le langage courant, le terme diffusion fait référence à une notion de...), comme la diffusion de Rutherford qui se traite via la symétrie de Corinne.

Propriétés générales

Pour obtenir les principales caractéristiques d'un mouvement à force centrale, il n'est pas nécessaire que cette force $\vec F$ dérive d'une énergie potentielle^[1] comme c'est le cas de plusieurs types de forces comme la force coulombienne.

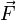
Planéité de la trajectoire

Le théorème (Un théorème est une proposition qui peut être mathématiquement démontrée, c'est-à-dire une...) du moment cinétique appliqué au centre de force O donne:

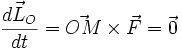
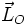
$\frac{\vec{dL_{O}}}{dt}=\vec{OM}\times \vec{F}=\vec{0}$ , où $\vec L_{O}$ est le moment cinétique au point O.

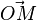
Par conséquent, le moment cinétique est constant au cours du mouvement^[2]. Il s'en suit que le vecteur (En mathématiques, un vecteur est un élément d'un espace vectoriel, ce qui permet...) position $\vec{OM}$ et la quantité de mouvement (En physique, la quantité de mouvement est la grandeur physique associée à la vitesse et la masse...) $\vec{p}$ du point M sont à tout (Le tout compris comme ensemble de ce qui existe est souvent interprété comme le monde ou...) instant (L'instant désigne le plus petit élément constitutif du temps. 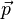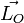L'instant n'est pas...) perpendiculaires à un vecteur de direction constante : la trajectoire est donc plane, entièrement contenue dans le plan perpendiculaire à $\vec{L_{O}}$ .

Le mouvement peut donc être étudié uniquement dans ce plan sur lequel on choisit les coordonnées polaires (Les coordonnées polaires sont, en mathématiques, un système de coordonnées...) r et $θ$ pour indiquer la position du point M. On peut alors montrer que la norme (Une norme, du latin norma (« équerre, règle ») désigne un...) constante du moment cinétique vaut :

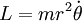
$L = mr^{2}\dot{\theta}$ .

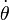
Ceci implique directement que le signe de $\dot{\theta}$ reste identique au cours du mouvement : le point M décrit toujours la trajectoire dans le même sens.

Loi des aires

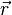
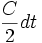
On peut montrer que l'aire (Aires (en espagnol, les airs) est une compagnie aérienne intérieure de Colombie.) balayée par le vecteur position $\vec{r}$ pendant un temps dt vaut $\frac{C}{2}dt$ où C est une constante, appelée constante des aires donnée (Dans les technologies de l'information, une donnée est une description élémentaire,...) par :

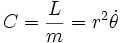
$C = \frac{L}{m} =r^2\dot\theta$ .

Autrement dit, la vitesse aérolaire est une constante autour du mouvement.

Cette loi des aires fut énoncée de façon empirique pour la première fois en 1609 par Johannes Kepler (Johannes Kepler (ou Keppler), né le 27 décembre 1571 à Weil der Stadt dans...) d'après le mouvement des planètes autour du Soleil (Cf. lois de Kepler). C'est en réalité une propriété générale de tout mouvement à force centrale.

Elle implique notamment que $θ = f (t)$ est fonction strictement monotone du temps. Il existe donc une fonction réciproque (La réciproque est une relation d'implication.) $t = f - 1 (θ)$ . C'est-à-dire que pour un angle (En géométrie, la notion générale d'angle se décline en plusieurs concepts...) donné, il est possible de déterminer le temps correspondant^[3]. La fonction réciproque de l'équation (En mathématiques, une équation est une égalité qui lie différentes quantités, généralement...) du temps de Kepler posa par exemple de beaux problèmes mathématiques à Legendre et Cauchy.

Expression de l'énergie cinétique (L'énergie cinétique (aussi appelée dans les anciens écrits vis viva, ou force vive) est...), effet centrifuge

Le calcul de l'énergie cinétique du point matériel M donne son expression :

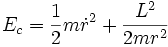
$E_c=\frac{1}{2}m\dot{r}^{2}+\frac{L^{2}}{2mr^{2}}$ .

qui se décompose en deux termes :

le premier est celui d'une particule de masse (Le terme masse est utilisé pour désigner deux grandeurs attachées à un...) m effectuant un mouvement unidimensionnel (selon la direction de r),
le second est analogue à une énergie potentielle coulombienne répulsive qui agit comme une force centrifuge.

Cas d'une force centrale conservative

Pour simplifier le problème, on peut choisir une force centrale conservative, c'est-à-dire qu'elle dérive d'une énergie potentielle^[4] V par la formule :

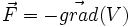
$\vec F=-\vec{grad}(V)$ .

C'est le cas, par exemple, du mouvement des planètes autour du soleil.

Energie potentielle effective

D'après la loi de conservation (En physique, une loi de conservation (rien ne se perd, rien ne se crée) exprime qu'une propriété...) de l'énergie, l'énergie totale $E = E c + V$ est une constante. Compte tenu de l'expression précédente de l'énergie cinétique, cette énergie totale se met sous la forme :

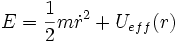
$E=\frac{1}{2}m\dot{r}^{2}+U_{eff}(r)\quad$ où $\quad U_{eff}(r)= V(r)+\frac{L^{2}}{2mr^{2}}$ est appelée l'énergie potentielle effective.

Le phénomène est donc analogue à un mouvement unidimensionnel d'une particule fictive de masse m dans un potentiel $U e f f (r)$ . Ce potentiel fait apparaître, en plus de V, la force centrifuge introduite plus haut. Cela correspond donc à une compétition entre deux forces : par exemple, dans le cas du mouvement d'une planète (Une planète est un corps céleste orbitant autour du Soleil ou d'une autre étoile de...), il y a compétition entre l'attraction vers le soleil, et la force centrifuge.

Cas d'un champ (Un champ correspond à une notion d'espace défini:) attractif

Dans le cas d'un champ attractif, le potentiel effectif U_eff(r) présente un puits de potentiel : il est fortement répulsif à courte distance d'après la "barrière centrifuge", et attractif à longue distance. Et comme $r 2$ est toujours positif, on a nécessairement l'inégalité suivante :

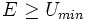
$E \ge U_{min}$ ,

où $U m i n$ est la valeur minimale prise par le potentiel effectif (à la distance r_m).

Le mouvement est alors différent selon les valeurs de E_m.

Si $E \ge 0$ , le corps peut s'éloigner à l'infini (Le mot « infini » (-e, -s ; du latin finitus,...) (mouvement non-borné)^[5].
Si $U_{min} < E \le 0$ , le mouvement est borné entre les positions r_min et r_max. Le mouvement radial (selon r) est alors périodique : il présente une oscillation (Une oscillation est un mouvement ou une fluctuation périodique. Les oscillations sont soit à...) entre r_min et r_max.
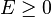
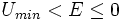
Si $E = U m i n$ , la trajectoire est circulaire de rayon r_m quelle que soit V(r).
Si $E < U m i n$ , le mouvement est impossible. En fait, dans le cas du champ coulombien attracteur (Dans l'étude des systèmes dynamiques, un attracteur (ou ensemble-limite) est un ensemble, une...), cette situation (En géographie, la situation est un concept spatial permettant la localisation relative d'un...) correspondrait à une énergie mécanique (L'énergie mécanique est une quantité utilisée en mécanique classique pour désigner l'énergie...) initiale insuffisante pour "satelliser" la particule.

Expressions générales des équations horaire et polaire

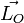
Le mouvement à force centrale conservative possède trois degrés de liberté : les coordonnées r et $θ$ dans le plan du mouvement, et le temps t. De plus il existe deux constantes du mouvement : le moment cinétique $\vec{L_{O}}$ et l'énergie mécanique (Dans le langage courant, la mécanique est le domaine des machines, moteurs, véhicules, organes...) $E$ . Le problème possède alors une solution exacte qu'il est possible d'obtenir^[6].

La solution peut s'écrire, soit par une équation horaire (r(t)), soit par une équation polaire (r(θ)). En effet, la loi des aires vue (La vue est le sens qui permet d'observer et d'analyser l'environnement par la réception et...) plus haut montre qu'il est possible d'interchanger t et θ. On étudie brièvement ces deux possibilités :

En exprimant la conservation de l'énergie, on obtient une équation différentielle de Newton qui a pour solution :

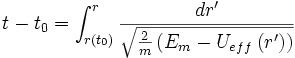
$t-t_{0}=\int_{r\left (t_{0}\right )}^{r}{\frac{dr'}{\sqrt{\frac{2}{m}\left (E_{m}-U_{eff}\left (r' \right ) \right )}}}\,$ .

Par inversion il est possible d'obtenir la forme analytique de r(t). On peut alors utiliser cette valeur pour calculer

θ(t)

grâce à la constante des aires. Finalement, les lois horaires r(t) et θ(t) donnent l'équation paramétrée de la trajectoire en coordonnées polaires.

Si l'on ne cherche que la trajectoire, et pas l'évolution du mouvement dans le temps, on peut éliminer le temps t pour le remplacer par θ en utlisant la loi des aires. On obtient alors une autre équation différentielle de Newton dont l'on peut aussi trouver la solution :

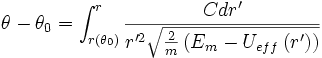
$\theta-\theta_{0} =\int_{r\left (\theta_{0} \right )}^{r}{\frac{Cdr'}{r'^{2}\sqrt{\frac{2}{m}\left (E_{m}-U_{eff}\left (r' \right ) \right )}}}$ .

On obtient ainsi l'équation polaire

r (θ)

, c’est-à-dire l'équation de la trajectoire en coordonnées polaires.

Ces expressions intégrales peuvent être très complexes à évaluer directement. Dans certains cas, notamment celui du problème à deux corps, des techniques de résolutions plus simples que celle de l'évaluation explicite de l'intégrale (Une intégrale est le résultat de l'opération mathématique, effectuée sur une fonction, appelé...) peuvent être utilisées.

Possibilités d'orbites fermées

Dans le cas d'un mouvement borné, le mouvement radial (r(t)) est périodique, de période T_r. D'après le paragraphe précédent, l'équation horaire donne l'expression suivante :

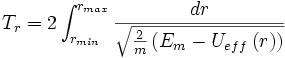
$T_{r}=2\int_{r_{min}}^{r_{max}}{\frac{dr}{\sqrt{\frac{2}{m}\left (E_{m}-U_{eff}\left (r \right ) \right )}}}\,$ ,

où $r m i n$ et $r m a x$ sont les rayons minimum et maximum accessibles.

Cela ne signifie pas que le mouvement global est périodique, donc que la trajectoire est une courbe (En géométrie, le mot courbe, ou ligne courbe désigne certains sous-ensembles du...) fermée. En effet il faudrait pour cela qu'au bout d'un nombre (La notion de nombre en linguistique est traitée à l’article « Nombre...) entier n de périodes radiales T_r, l'angle θ ait effectué un nombre entier p de tours complets. On dit aussi que la période angulaire T_ang doit être commensurable avec la période radiale T_r^[7].

Or la variation $Δθ$ de l'angle polaire θ pendant la période radiale T_r s'exprime par :

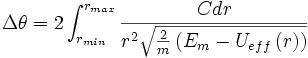
$\Delta\theta =2\int_{r_{min}}^{r_{max}}{\frac{Cdr}{r^{2}\sqrt{\frac{2}{m}\left (E_{m}-U_{eff}\left (r \right ) \right )}}}$ .

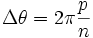
D'après ce qui précède, la trajectoire sera fermée si et seulement si on a $\Delta\theta=2\pi\frac{p}{n}$ . Ceci n'est vérifié, pour les champs conservatifs, que par deux types de forces centrales : la force en 1/r² (de type coulombien) et la force de rappel élastique (ce résultat constitue le théorème de Bertrand).

Remarques techniques

L'existence de trajectoires fermées est associée à une symétrie, ce qui se manifeste par l'existence d'une constante du mouvement additionnelle. Par exemple, pour le champ coulombien, il s'agit de l'invariant de Runge-Lenz.
En mécanique quantique (La mécanique quantique est la branche de la physique qui a pour but d'étudier et de...), les champs présentant classiquement des orbites fermées exhibent une dégénérescence accidentelle de leurs niveaux d'énergie. Par exemple, pour le champ coulombien, alors que la théorie (Le mot théorie vient du mot grec theorein, qui signifie « contempler, observer,...) générale prévoit des niveau E_n,l, on obtient des niveau E_n ne dépendant que d'un seul nombre quantique (Un nombre quantique est, en mécanique quantique, un élément d'un jeu de nombres permettant de...). L'origine est une symétrie additionnelle du champ coulombien vis-à-vis des rotations de l'espace à 4 dimensions (Dans le sens commun, la notion de dimension renvoie à la taille ; les dimensions d'une pièce...) (groupe O(4))^[8].
Soit P la projection (La projection cartographique est un ensemble de techniques permettant de représenter la surface de...) de O sur la tangente à la trajectoire de M. La trajectoire de P est appelée la podaire de O. L'inverse de la podaire donne, à une rotation près, ce que l'on appelle l'hodographe. Réciproquement, l'antipodaire de l'inverse de la podaire redonne la trajectoire. Ainsi, l'orbite (En mécanique céleste, une orbite est la trajectoire que dessine dans l'espace un corps...) de l'espace des phases (L'espace des phases est un espace abstrait dont les coordonnées sont les variables dynamiques du...), dont la projection sur (O, x, y) est la trajectoire et dont la projection sur l'espace des vitesses (O, Vx, Vy) est l'hodographe, est donc très particulier. Newton accordant une attention toute particulière aux podaires et antipodaires. À cette époque, tout le monde (Le mot monde peut désigner :) savait que l'inverse d'un cercle (Un cercle est une courbe plane fermée constituée des points situés à égale...) était un cercle et l'antipodaire d'un cercle une ellipse. À une trajectoire elliptique de Kepler correspondait donc un hodographe circulaire. D'une manière ou d'une autre, les lois de Kepler ont été démontrées via cet hodographe circulaire. Plusieurs scientifiques pourraient être à l'origine de cette découverte : Newton dans ses brouillons perdus, comme il l'affirme en août 1684 à Halley, Hermann (1678 - 1733) dont on voit la démonstration (En mathématiques, une démonstration permet d'établir une proposition à partir...) dans la troisième édition des Principia, etc.

Notes et références

↑ Certaines forces ont un caractère "central" sans dériver d'une énergie potentielle : par exemple la force de tension (La tension est une force d'extension.) du fil dans le pendule simple (En physique, le pendule simple est une masse ponctuelle fixée à l'extrémité...).
↑ Fondamentalement, le fait que le moment cinétique soit constant vient de la symétrie centrale SO(3), voir théorème de Noether.
↑ C'est empiriquement ce que fait un cadran solaire (Un cadran solaire est un instrument silencieux et immobile qui indique le temps solaire par le...) analemmatique.
↑ Cette énergie potentiel ne dépend que de r car la force est centrale, et tend souvent vers 0 à l'infini.
↑ Cela exclut tout potentiel attractif qui ne tend pas vers une constante à l'infini.
↑ Voir Landau et Lifchitz, Physique théorique T1: Mécanique, 5^ème édition Française, Ellipses-Marketing, 1994.
↑ On a alors dégénerescence du mouvement, voir Landau, op. cit., paragraphe 52.
↑ Voir Landau et Lifchitz, Physique théorique T3: Mécanique quantique, Mir, Moscou (), 1988.

Cet article vous a plu ? Partagez-le sur les réseaux sociaux avec vos amis !

Actualités

...

Il y a 9 heures | Vie et Terre

Le lien entre diversité génétique et adaptation par sélection naturelle

...

Il y a 13 heures | Astrophysique

Concentration d'une multitude de trous noirs

...

Il y a 1 jour | Vie et Terre

Le réseau écologique sombre, un nouveau concept pour lutter contre la pollution lumineuse

...

Il y a 1 jour | Vie et Terre

Vidéo: Les oiseaux marins détoxifient le mercure ingéré dans leur alimentation

...

Il y a 1 jour | Vie et Terre

L'invasion des perruches

...

Il y a 1 jour | Physique

Nouvelles perspectives sur le mécanisme de la fission nucléaire

...

Il y a 2 jours | Vie et Terre

Comment les cyanobactéries "caméléons" ont acquis la capacité de changer de couleur

...

Il y a 2 jours | Physique

Le rôle surprenant de l'eau dans le séchage du bois

...

Il y a 2 jours | Vie et Terre

Pollution aquatique: explorer la piste du lipidome chez les crustacés d'eau douce

...

Il y a 2 jours | Autres sujets

Des chaussures qui font courir un peu plus vite ?

Voir aussi

Nouvelles perspectives sur le mécanisme de la fission nucléaire

Le rôle surprenant de l'eau dans le séchage du bois

Déplacer un objet macroscopique grâce à un système quantique

Une intrication peut en cacher une autre !

Page générée en 0.178 seconde(s) - site hébergé chez Amen
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
Ce site est édité par Techno-Science.net - A propos - Informations légales
Partenaire: HD-Numérique