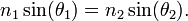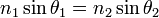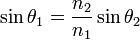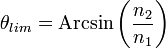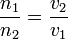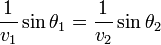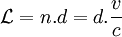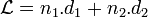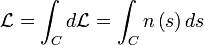Réfraction - Définition
En physique des ondes — notamment en optique, acoustique et sismologie — le phénomène de réfraction est la déviation d'une onde lorsque la vitesse de celle-ci change entre deux milieux. Typiquement, cela se produit à l'interface entre deux milieux, ou lors d'un changement d'impédance du milieu.
On peut représenter une telle onde par deux approches :
- par son front d'onde : c'est la ligne que décrit une vague dans l'eau (optique ondulatoire et sismologie) ;
- par un rayon : c'est la direction de propagation de l'onde, perpendiculaire au front d'onde (optique géométrique).
Les deux modèles sont équivalents dans le cas de la réfraction, cependant on préfèrera le premier pour expliquer le phénomène, et le second pour le quantifier.
Description

La lumière est déviée lorsqu'elle passe d'un milieu transparent à un autre (par exemple : de l'air à l'eau, ou le contraire…). C'est ce phénomène qu'on observe lorsque l'on regarde une paille dans un verre : celle-ci paraît brisée. Cette fracture apparente est à l'origine du mot réfraction.
La lumière est dite " réfractée " et la propriété qui caractérise les différents milieux transparents est la " réfringence ", qui se traduit par une valeur numérique : l’ " indice de réfraction ".
Approche géométrique : Loi de Snell-Descartes
Seule la seconde loi de Snell-Descartes concerne la réfraction.
Chaque milieu transparent est caractérisé par son indice de réfraction noté ni . On appelle dioptre la surface séparant les deux milieux.
Les lois de la réfraction, énoncées par Snell et Descartes, permettent de rendre compte quantitativement du phénomène. Pour la réfraction, les lois de Snell-Descartes précisent que :
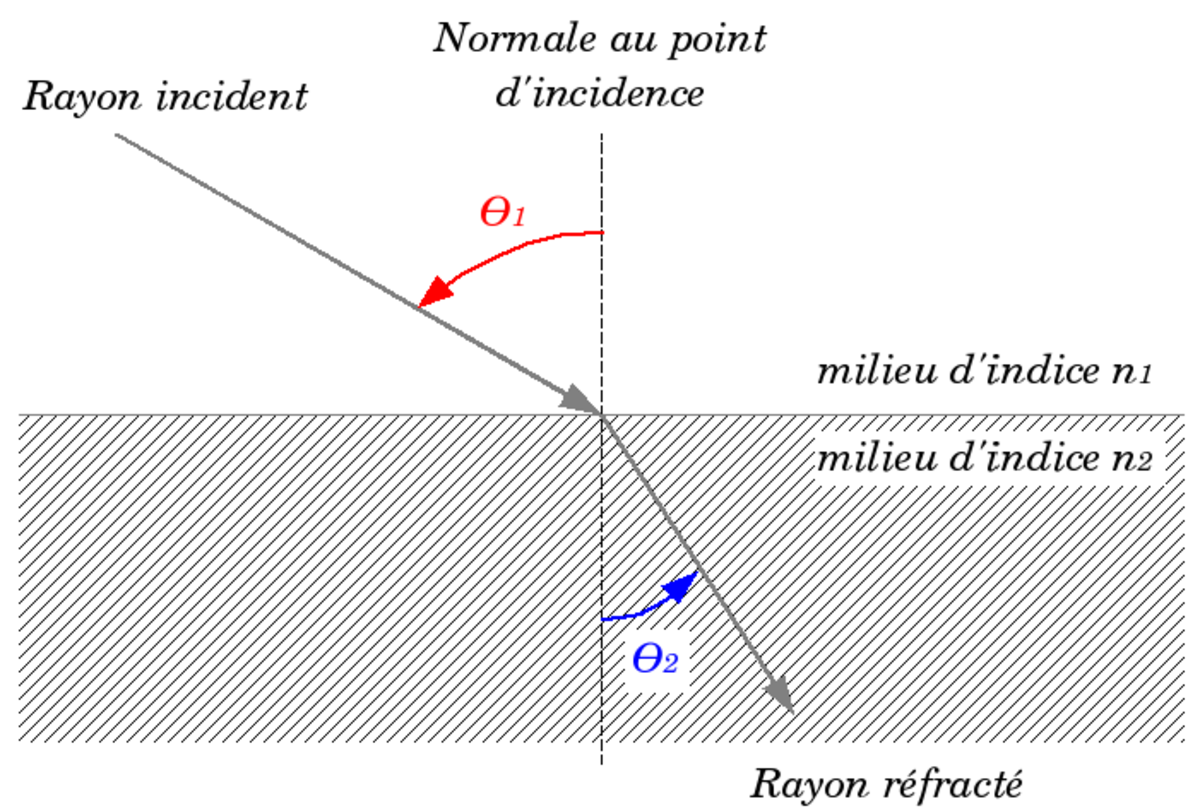
- Le rayon réfracté se situe dans le plan d'incidence (défini par le rayon incident et la normale au dioptre au mouvement d'incidence), rayon incident et rayon réfracté étant de part et d'autre de la normale ;
- Les angles d'incidence et de réfraction (θ1) et (θ2), mesurés par rapport à la normale sont tels que :
|
|
On peut alors remarquer que :
- Plus l'indice de réfraction n2 est grand, plus le rayon réfracté s'approche de la normale, et vice versa ;
- Lorsque l'indice de réfraction n2 est plus petit que n1 (par exemple : du verre à l'air), on peut dépasser une incidence dite " angle critique " au delà de laquelle il y a réflexion totale.
Interprétation de l'expérience du " crayon brisé "
L'explication de l'expérience du crayon brisé repose sur deux points importants : les lois de Snell-Descartes, et la propriété de stigmatisme approché du dioptre plan permise par l'œil, qui n'intercepte qu'un fin pinceau de lumière réfractée.
On constate alors que, les rayons étant réfractés en s'écartant de la normale, puisque l'indice de l'air est inférieur à l'indice de l'eau, la lumière qui arrive dans l'œil de l'observateur semble provenir d'un point plus élevé.
Le schéma ci-contre illustre pour un point de l'extrémité du crayon. Il faudrait faire ainsi pour chacun des points pour avoir l'image (au sens du stigmatisme approché) du crayon. (L'effet d'un dioptre est aussi de donner une image déformée).
On peut énoncer certaines remarques :
- L'image de l'extrémité du crayon n'est pas à la verticale de celle du crayon lui-même (contrairement à certaines schématisations rapides) ;
- L'image de l'extrémité du crayon dépend de la position de l'observateur (conséquence immédiate du non stigmatisme du dioptre).
Angle limite de réfraction
Si n1 > n2 (par exemple passage de l'eau vers l'air), alors d'après la loi de Snell-Descartes :
donc :
Pour des valeurs de sin(θ2) proches de 1, c'est-à-dire pour des incidences rasantes (rayon incident proche de la surface), la loi de Snell-Descartes donne une valeur de sin(θ1) supérieure à 1. On sort en effet de son domaine de validité : cela correspond à des situations où il n'y a pas de réfraction mais uniquement de la réflexion, on parle de " réflexion totale ".
L'angle limite [1] de réfraction est donc :
Cette propriété est mise à profit dans certains systèmes réflecteurs (prisme à réflexion totale) et les fibres optiques.
Construction de Descartes
La relation de Snell-Descartes peut être traduite géométriquement. Ceci permet une construction géométrique simple (dite de Descartes) du rayon réfracté.
Cette construction repose sur le tracé des " cercles des indices ". On trace les deux cercles de rayon ρ1 = n1 et ρ2 = n2 centrés sur le point d'incidence (I). Le rayon incident (provenant du milieu 1) est prolongé dans le milieu 2 et coupe le cercle 1 en un point A dont la projection H est telle que, par construction, IH = n1sini.
Pour satisfaire la relation de Snell-Descartes, le rayon réfracté doit couper le cercle 2 en un point B ayant même projection. Il suffit donc de prolonger la droite (AH) jusqu'à son intersection avec le cercle 2.
Approche ondulatoire : Principe de Huygens-Fresnel
La célérité de la lumière n'est pas la même dans les deux milieux. Ce changement de valeur suffit à interpréter le changement de direction de l'onde. C'est Christiaan Huygens qui, le premier, a donné un modèle, en associant la propagation de la lumière à la propagation d'un front d'onde.
Le principe de Huygens-Fresnel
Le principe de Huygens-Fresnel stipule qu'à une interface, tous les points atteints par une onde venant d'un premier milieu réémettent une onde dans le second milieu. On peut alors interpréter la réfraction comme la déviation du front d'onde liée à la vitesse plus faible (ou plus rapide) de ces ondes réémises.
Huygens — s'opposant ainsi à Newton — considérait que la lumière était une onde, se propageant de proche en proche dans les milieux transparents. Il imaginait le front d'onde comme la superposition d'ondelettes, de sorte qu'au passage d'un dioptre, la célérité étant différente de part et d'autre, la taille des ondelettes était changée d'autant et le front dévié en conséquence. Le rapport des indices des milieux apparaît alors simplement comme le rapport des célérités :
On peut également utiliser ce même principe pour rendre compte de la réflexion (il suffit en effet de considérer la partie des ondelettes se déployant dans le premier milieu) et de la diffraction.
Construction de Huygens du rayon réfracté
Cette interprétation permet également une construction géométrique. Celle-ci est semblable à celle de Descartes, mais elle s'appuie sur la comparaison des célérités.
Les rayons à tracer sont alors en 1/n1 et 1/n2 et le raisonnement géométrique repose sur l'intersection commune des plans d'onde (point B), qui, par nature doivent être tangents aux ondelettes.
L'ondelette la plus grande correspond sur la figure à la position du front d'onde s'il n'y avait pas de dioptre (ici n2 > n1), tandis que le cercle le plus petit correspond donc au front de l'onde diffractée.
Le rayon réfracté est donc bien selon (IC) (I étant le point d'incidence).
Approche du " moindre parcours " : principe de Fermat
Un aspect particulièrement étonnant est la possibilité d'interpréter également ces lois de Snell-Descartes en terme de moindre parcours, et plus précisément en terme de moindre temps.
C'est Fermat qui a introduit cette interprétation, source tout à la fois pour lui de questionnements fondamentaux sur la " raison " de ce moindre parcours, et d'une approche théorique très puissante dite de moindre action.
Énoncé du principe de Fermat :
- " La lumière se propage d'un point à un autre sur des trajectoires telles que la durée du parcours soit stationnaire. "
Là encore, une analogie " mécanique " peut aider à comprendre pourquoi durée de parcours et trajectoire brisée sont intimement liées.
Considérons maintenant un athlète devant partir d'un point de la plage et rejoindre le plus vite possible une bouée située dans l'eau. Là encore, l'athlète court plus vite sur la plage qu'il ne progresse dans l'eau. En conséquence, il convient donc de ne pas aller en ligne droite vers la bouée, mais de rallonger la distance parcourue sur le sable (et diminuer celle à parcourir dans l'eau). Mais évidemment, il ne faut pas non plus trop rallonger sur le sable…
On peut alors chercher quel est le chemin qui correspond au minimum de temps. C'est un chemin tel que le point d'arrivée au bord de l'eau n'est ni l'intersection avec la ligne droite, ni le cas où la distance dans l'eau est la plus faible (en nageant perpendiculairement à la rive) mais un point entre les deux, et qui est tel que :
On retrouve l'expression de la loi de la réfraction.
Chemin optique
Lorsqu'un rayon parcourt une distance d dans un milieu d'indice n, on appelle chemin optique, et on note L, le produit de la distance et de l'indice :
Si un rayon change de milieu et parcourt une distance d1 dans un milieu d'indice n1 et une distance d2 dans un milieu d'indice n2, alors le chemin optique parcouru est :
On remarque alors que le chemin que parcourt un rayon pour aller d'un point à un autre correspond toujours à un extrémum de L (minimum ou parfois maximum) : ligne droite dans un milieu donné, et réfraction suivant la loi de Snell-Descartes lorsqu'il change de milieu. C'est ce que l'on appelle un principe de moindre action.
Notez qu'il s'agit là d'une constatation, d'une conséquence, et non d'une cause. Le rayon lumineux n'a pas de stratégie, il ne décide pas d'emprunter tel ou tel chemin, et le point d'arrivée n'est pas donné à l'avance ! Mais ce principe est très puissant et peut être généralisé à beaucoup d'approches de la physique. En optique, il permet de calculer le trajet dans un milieu d'indice variable.
Milieux d'indice variable
On a jusqu'ici considéré des milieux homogènes et isotropes, dans lesquels la vitesse de la lumière était la même partout et dans toutes les directions. Mais il existe des milieux dans lesquels la vitesse de la lumière, donc l'indice de réfraction, varie de manière continue, par exemple l'air.
Si le sol est chaud, alors la température de l'air diminue lorsque l'on s'élève en altitude. La densité de l'air varie, et la vitesse de la lumière, donc l'indice, aussi (gradient d'indice) ; c'est ainsi que le bitume par temps très chaud déforme les images ou fait apparaître d'imaginaires flaques d'eau reflétant le ciel (concavité vers le haut du trajet lumineux) et qu'on peut apercevoir une oasis dans le désert bien qu'elle soit derrière une dune (concavité vers le bas dans ce cas), mais le terme de " mirage " s'applique aussi à l'effet du soleil sur l'imagination du voyageur.
Une autre expérience commune consiste à prendre un aquarium rempli d'eau et mettre du sel au fond : la concentration de sel est plus importante au fond qu'en surface, et l'indice de réfraction varie en fonction de cette concentration ; un rayon laser passant dans un aquarium contenant un peu de fluorescéine peut alors donner (??) courbe (et non plus une ligne droite).
Enfin, dans les fibres optiques, on fait volontairement varier l'indice de réfraction en fonction de la distance par rapport au centre de la fibre ; dans ce cas la variation d'indice sert à " piéger " le rayon lumineux qui ondule et suit la fibre plutôt que de se réfléchir sur les bords.
Dans ces milieux, l'indice n dépend donc du point considéré, n est une fonction de la position (x,y,z) (Voir la fonction gradient).
Chemin optique total
Le trajet du rayon lumineux est une courbe C dans le milieu. Considérons un petit trajet du point s au point s+ds sur lequel l'indice peut être considéré comme constant (s est l'abscisse curviligne sur C, c'est-à-dire la distance parcourue en suivant la courbe depuis le point de départ). Le chemin optique est localement :
le chemin optique total est donc :
D'après le principe de moindre action, le trajet suivi par le rayon lumineux correspond à celui qui a la valeur L minimale. Ceci permet de calculer la trajectoire du rayon.
Réfraction des ondes mécaniques
De façon générale, et donc en mécanique, la propagation suit les mêmes lois fondamentales, en particulier le fait que la célérité ne dépend que du milieu : son élasticité et son inertie. Les phénomènes de réflexion, réfraction, diffraction et interférences existent donc également pour ces ondes. Suivant le nombre de dimensions spatiales offertes par le milieu à la propagation, tout ou partie de ces phénomènes sont visibles.
Ainsi pour une propagation unidimensionnelle (une onde le long d'une corde par exemple) il est facile d'observer la réflexion, et possible d'expérimenter la transmission (avec réflexion partielle) entre deux cordes de masses linéiques différentes. Pour les ondes à la surface de l'eau, les phénomènes de réflexion, réfraction et diffraction sont faciles à observer. Quant aux ondes acoustiques qui nous entourent, leur propagation en trois dimensions jusqu'à notre oreille est bien souvent le fruit de tous ces phénomènes à la fois.
Ondes à la surface de l'eau
Les équations régissant les ondes dans l'eau ne sont pas linéaires. La célérité des ondes de surface dépend de la profondeur du liquide, de la vitesse du courant et de leur amplitude. En particulier la célérité est plus faible si la profondeur est plus faible. Ceci permet d'avoir une première interprétation du fait que les crêtes des vagues deviennent presque parallèles à la plage lorsqu'elles se rapprochent du rivage : la partie de la crête en eau plus profonde se propage plus vite que la partie en eau peu profonde et la crête tourne vers la plage.
Ce changement de célérité est donc précisément la cause du changement de direction de propagation d'une onde plane comme l'explique le principe de Huygens évoqué ci-dessus.
L'observation de ce phénomène peut-être réalisée sur une " cuve à ondes " [2]: un bac plat contient une faible hauteur d'eau (de l'ordre du centimètre). Sur une partie du fond du bac, on place une plaque qui provoque donc une brusque variation de la profondeur. Une onde plane (provoquée par la vibration d'une barre qui affleure l'eau) est alors déviée au passage de ce dioptre.
Réfraction des ondes sonores
Les ondes sonores subissent aussi une telle déviation. Dans l'atmosphère la vitesse du son varie avec la pression et la température(donc l'altitude), l'humidité et la vitesse du vent. Le phénomène de variation de la température avec l'altitude, appelé gradient de température, a pour effet d'incurver les rayons sonores vers le haut en temps normal, c’est-à-dire lorsque la température diminue avec l'altitude, et vers le bas lors d'une inversion de température. C'est pour cette raison que le son remonte les pentes, phénomène souvent audible en montagne.
De la même façon lorsque la vitesse du vent augmente avec l'altitude les rayons sonores sont réfractés vers le bas dans la direction du vent, et vers le haut dans la direction opposée au vent. C'est pour cela que le vent " porte le son ". C'est la variation du vent avec l'altitude (le gradient de vent) qui est importante et non la vitesse du vent elle même (bien plus faible que la vitesse du son).
Réfraction des ondes sismiques
La vitesse de propagation des ondes sismiques dépend de la densité, donc de la profondeur et de sa composition. Il se produit donc :
- une réfraction à la transition entre deux couches géologiques, notamment entre le manteau et le noyau ;
- dans le manteau, une déviation : c'est un milieu à indices variables.
Réfraction des ondes radio
Comme un rayon lumineux est dévié lorsqu'il passe d'un milieu d'indice de réfraction n1 à un autre d'indice n2, une onde radio peut subir un changement de direction dépendant à la fois de sa fréquence et de la variation de l'indice de réfraction. Ce phénomène est particulièrement important dans le cas de la propagation ionosphèrique, la réflexion que subit une onde décamétrique dans l'ionosphère est en fait une suite continue de réfractions. Il est possible de reproduire avec une onde radio dont la longueur d'onde est de quelques centimètres à quelques décimètres le phénomène observé avec une lentille ou un prisme en optique classique.
Observations optiques
- La Corse vue de Nice par phénomène optique de réfraction (explications scientifiques)