Moteur à allumage commandé - Définition

Combustion

Généralités

La combustion du mélange air-essence dans un moteur à combustion interne est une transformation chimique, une oxydation exothermique vive du carburant et du dioxygène. L'octane est généralement utilisé comme molécule permettant de décrire une combustion de ce type. L'équation générale en tout point de l'espace de la combustion est alors fournie par la formule suivante :

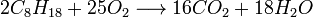
Pour être plus précis dans l'estimation de la réaction réelle, on prend les nombres molaires réels de l'analyse chimique du carburant. Le rapport théorique massique idéal air/essence pour le moteur à combustion interne est de 14,7:1, soit 14,7 g d'air pour 1 g de carburant. On parle alors de mélange stœchiométrique.

Il est important de préciser que cette équation suppose que le fluide est homogène en tout point de l'espace, ce qui n'est pas le cas dans la pratique. Il est difficile de modéliser intégralement la réaction de combustion qui se déroule dans la chambre, puisqu'il s'agit d'une combustion intermittente, i.e. qui dépend du temps, de la température et de la turbulence du phénomène. Une analyse informatique découpant le problème en périodes d'une microseconde est néanmoins capable de tenir compte de la température et du temps, mais ne peut rendre compte du phénomène de turbulence car le fluide s'en trouve modifié en tout point de l'espace.

Auto-inflammation

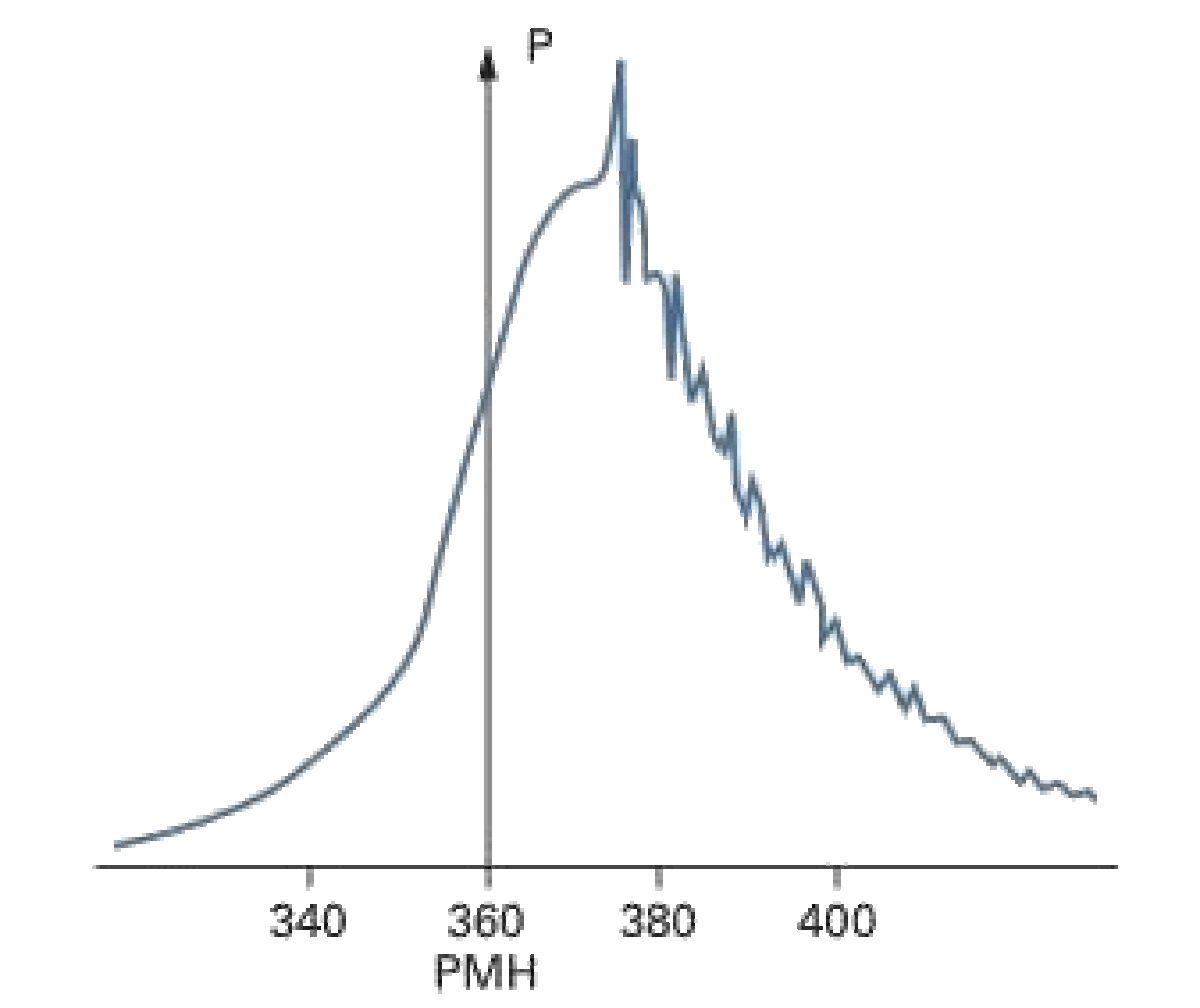
Comme le point d'auto-inflammation de l'essence – c'est-à-dire la température à laquelle l'essence s'enflamme spontanément sans l'apport d'une étincelle – est supérieur à la température de vaporisation et qu'il s'agit d'un liquide volatil, l'essence peut être aisément injectée à l'air pour former un « mélange pratiquement homogène, constant en qualité et en quantité pour un régime donné ». Pour réaliser la combustion, le mélange doit atteindre sa température d'inflammation, proche de 380 °C. Les pressions dans le mélange atteignent des niveaux supérieurs à 30 bars.

Un délai d'auto-inflammation, c'est-à-dire la durée durant laquelle les conditions de combustion sont optimales avant d'atteindre l'auto-inflammation, est généralement prédéfini. Il est important que le point mort haut ou PMH soit atteint durant ce délai, engendrant dans le cas contraire un phénomène de cliquetis. Une étude sur une machine à compression rapide permet d'obtenir le délai τ en fonction de la pression P, de la température T, et de constantes A, n et B dépendant de la composition de l'essence.

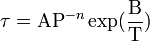
Lors d'un phénomène de cliquetis, le mélange comprimé et chauffé par rayonnement peut s'enflammer sans avoir été atteint par le front de flamme, provoquant une combustion beaucoup plus rapide qu'à la normale. Ce phénomène a pour conséquence des pics de pression dans la chambre, synonyme de bruit et de contraintes élevées dans le moteur. Le cliquetis est principalement dû à l'avance à l'allumage.

Contrôle des gaz d'échappement

Polluants émis

Lorsque la réaction du mélange air-essence est totale, les produits de combustion sont uniquement de l'eau et du dioxyde de carbone (CO). En pratique la combustion n'étant jamais complète, de nombreux hydrocarbures sont émis : des hydrocarbures partiellement brûlés tels que les aldéhydes, les cétones, les acides carboxyliques, les monoxydes de carbone (CO), mais également des produits de craquage thermique comme la suie, l'acétylène ou l'éthylène. Des polluants particulièrement nocifs pour la santé sont également émis, dont les plus connus sont les oxydes d'azotes (NO_x). Suite à une exposition au rayonnement solaire, des oxydants (peroxydes organiques, ozone, etc.) se forment après la sortie du pot d'échappement.

Même si les produits de la combustion de l'essence sont nombreux, l'eau, le dioxyde de carbone et l'azote sont largement majoritaires. Ces gaz ne sont pas dangereux – sauf l'azote lorsqu'il est oxydé en NO_x – mais le CO₂ est particulièrement gênant en raison de sa contribution au phénomène d'effet de serre.

Traitement des gaz d'échappement

Afin de diminuer les émissions de polluants, un pot catalytique est placé en sortie d'échappement du moteur. Comme son nom l'indique, il s'agit d'un catalyseur ayant pour but de traiter chimiquement les gaz d'échappement afin de les rendre moins nocifs. Deux types de catalyseurs existent et ont des rôles différents. Les catalyseurs d'oxydation, qui facilitent l'oxydation des monoxydes de carbone et des hydrocarbures, et nécessitent, de ce fait, un excès d'air pour fonctionner, ce qui induit un mélange pauvre ou implique l'insufflation d'air secondaire ; les catalyseurs de réduction facilitent, quant à eux, la réduction des oxydes d'azotes par déficit d'air.

L'ajout en série de ces deux types de catalyseurs se nomme « catalyseur à double lit ». Il permet de traiter efficacement l'ensemble des polluants émis par le moteur à allumage commandé. Les catalyseurs à double lit présentent l'inconvénient d'être onéreux, en raison d'un fonctionnement en mélange riche et de l'ajout d'un dispositif d'insufflation d'air secondaire. Une solution à ce problème réside dans l'utilisation d'un catalyseur à trois voies, régulé en boucle fermée en fonction de la richesse du mélange.

Modélisation

Les choix technologiques utilisés pour la conception du moteur à allumage commandé, tels que l'injection directe et les charges stratifiées ou homogènes, influent de façon significative sur la loi de combustion du mélange. Certains modèles se basent sur des lois empiriques, permettant d'établir facilement des relations de combustion, mais ne sont pas très exploitables par la suite, tandis que d'autres modèles font appel à des connaissances physiques de combustion. L'objectif de la modélisation est de définir la fraction brûlée de carburant en fonction de paramètres physiques (expérimentaux ou théoriques). Certains logiciels informatiques, tel que « Thermoptim », permettent de réaliser une modélisation assez réaliste.

Loi de dégagement d'énergie

L'une des premières modélisations de la combustion consiste à considérer les lois empiriques de dégagement de chaleur, en supposant le gaz homogène dans toute la chambre de combustion. Le premier principe de la thermodynamique établit que l'énergie interne d'un gaz est la somme du travail W et de la chaleur Q échangés. En considérant le temps, on peut donc aisément établir la relation suivante de dégagement d'énergie, où C_v est la capacité calorifique à volume constant, P la pression et V le volume de la chambre :

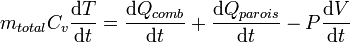
Une courbe de Wiebe – voir illustration ci-contre – permet de formaliser le taux de dégagement d'énergie par la fraction de carburant brûlée x_b en fonction de l'angle de rotation du vilebrequin θ, de l'angle de début d'allumage θ_all, de la durée de combustion Δθ_comb, ainsi que de paramètres a_v et m_v sur lesquels il est possible de jouer suivant les lois de combustion.

La valeur a_v désigne le pourcentage de masse de carburant brûlée par rapport à la masse introduite. Lorsque 99,9 % du carburant introduit est brûlé, a_v = 6,908. Plus la valeur de a_v est importante, plus la combustion est rapide et le pic de combustion important. La valeur de m_v influence quant à elle le dégagement de chaleur. En effet, lorsque m_v augmente, le pic de combustion est décalé et la combustion tardive. La loi de dégagement d'énergie est définie par deux indices : le CA50, angle du vilebrequin où 50 % de la masse est brûlée, et le HLC, hauteur de la loi de combustion. Ces indices sont déduits des valeurs empiriques de a_v et m_v.

Front de flamme

Généralités

Une approche plus physique de la combustion consiste à prendre en compte la propagation d'un front de flamme sphérique dans la chambre de combustion lors de l'allumage, ainsi que les phénomènes de turbulence. Le front de flamme se propage dans la chambre de combustion avec une vitesse de propagation, dénommée « vitesse de flamme laminaire » U_L dans le cas d'un mélange homogène, perpendiculaire au front de flamme. Cette vitesse dépend des propriétés du carburant ainsi que des phénomènes de diffusion de la chaleur. Une épaisseur de flamme δ, qui dépend de temps de combustion τ_comb et du coefficient de diffusion thermique d_th, est généralement définie :

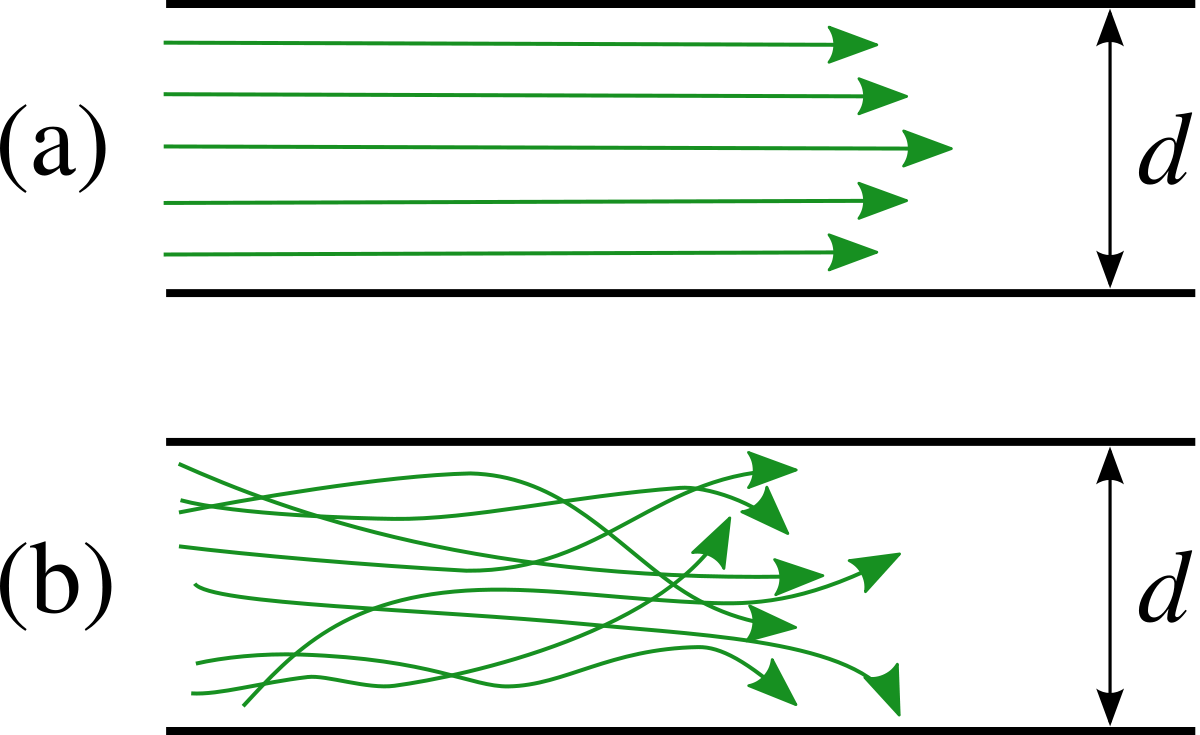
Dans le cas d'un écoulement turbulent, i.e. non laminaire, la vitesse U_T fluctue selon le champ turbulent, défini par le nombre de Reynolds Re (a fortiori de la viscosité ν) et la longueur de la turbulence l :

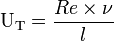
La combustion des gaz frais lors de la propagation du front de flamme est alors donnée par la formule suivante, définissant la masse de gaz brûlée en fonction de la surface du front A, de la masse volumique des gaz frais ρ et d'une masse imbrûlée de gaz χ entraînée par la flamme :

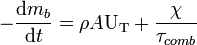
Modèle de McCuiston et Lavoie

Le modèle de propagation du front de flamme développée par McCuiston et Lavoie considère que la propagation du front dans la chambre est définie par deux temps caractéristiques : un temps lié à la combustion et un temps lié à l'entraînement des gaz frais dans la zone de combustion. Lorsque l'étincelle surgit de la bougie d'allumage, elle enflamme le mélange. Dès lors, une masse m_e de gaz frais est entraînée dans la zone de combustion selon une vitesse u_e, et est enflammée. Le présent modèle pose l'hypothèse que la distribution des fractions brûlées des masses entraînées est exponentielle :

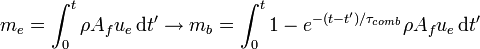
avec A_f, la surface du front de flamme et ρ, masse volumique des gaz frais.