Vecteur - Définition

Utilisations des vecteurs

Les exemples cités dans cet article sont relativement simples et didactiques. D'autres cas, plus généraux sont présentés dans les articles théorème spectral et algèbre linéaire.

Mathématiques

Représentation graphique d'un point dans le plan complexe. Les coordonnées cartésiennes correspondent à celle d'un point dans le repère de centre zéro et de base les nombres un et l'unité imaginaire.

Une vaste partie des mathématiques utilise les vecteurs, en algèbre, en géométrie ou en analyse.

Un exemple archétypal en algèbre est la résolution d'un système d'équations linéaires. Un exemple de trois équations à trois inconnues correspond à la recherche des vecteurs de dimension trois, antécédents d'une application linéaire d'un vecteur donné. Le plan euclidien peut aussi être représenté par le plan complexe. La base canonique est composée de deux vecteurs l'unité des réels et l'unité imaginaire.

Les vecteurs offrent un outil efficace pour la résolution de nombreux problèmes de géométrie. Ils sont utilisés pour la détermination de propriétés de parallélisme ou d'orthogonalité de droites, plan ou segments. À travers l'utilisation des coordonnées barycentriques, les vecteurs forment un outil adapté pour caractériser le centre d'une figure géométrique et permettent une démonstration simple du théorème de Leibniz, du théorème de Ceva comme de nombreux résultats sur la géométrie du triangles. Le produit scalaire, qui s'exprime particulièrement simplement dans une base orthonormée, offre de nombreuses possibilités. Il permet, par exemple, de mesurer la distance d'un point à une droite ou à un plan. Une telle base permet d'exprimer aussi simplement des transformations géométriques comme la projection orthogonale sur un plan ou une droite.

L'analyse n'est pas en reste. L'espace vectoriel R ², copie du plan euclidien est le cadre naturel de représentation du graphe d'une fonction. Les vecteurs permettent par exemple de déterminer la droite perpendiculaire à une courbe en vue de déterminer les foyers d'une conique. La représentation graphique offre une solution pour déterminer une approximation d'une racine d'une équation dans le cas où une résolution par une méthode algébrique n'est pas connue.

Physique

La trajectoire des planètes se modélise dans un langage vectoriel. Les travaux d'Isaac Newton sur cette question sont à l'origine du mot vecteur.

En présence d'un champ magnétique, des petites boussoles s'orientent, indiquant la direction et le sens des vecteurs du champ.

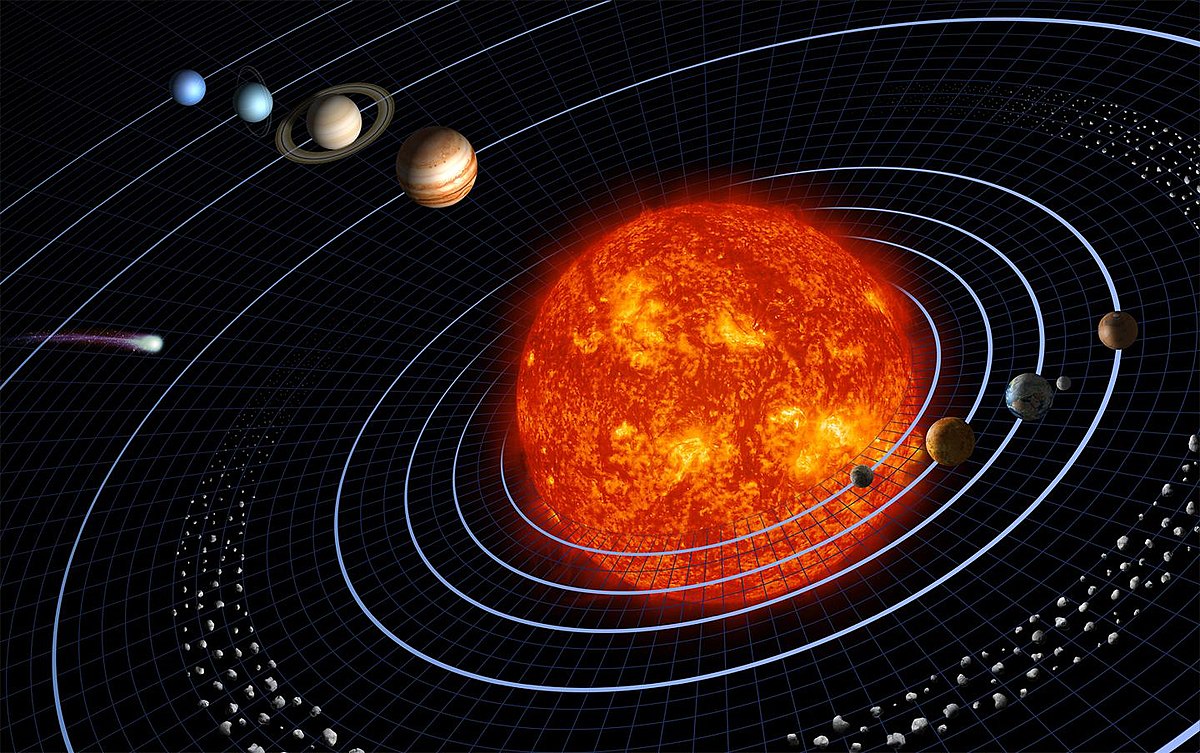
La physique est à l'origine du terme de vecteur, elle utilise toujours largement ce concept. La raison historique provient du fait qu'en physique classique l'espace qui nous entoure est bien modélisé comme espace affine (géométrie euclidienne) de dimension trois avec le temps (absolu) comme paramètre d'évolution. En physique, une addition de vecteurs ne peut avoir de sens que si leurs coordonnées respectives ont la même dimension.

La position d'un point est décrite par des coordonnées dans un repère, mais sa vitesse et son accélération sont des vecteurs. Pour établir la mécanique du point, c'est-à-dire l'étude des mouvements d'un point matériel, les vecteurs sont indispensables. La position d'un point se modélise par ses trois coordonnées (qui sont des nombres réels) dont chacune est une fonction du temps ; on peut aussi la décrire par le vecteur position allant de l'origine du repère au point : les composantes du vecteur sont alors identifiables aux coordonnées du point. Le vecteur vitesse est égal à la dérivée du vecteur position (c'est-à-dire : les composantes du vecteur vitesse sont les dérivées de celles du vecteur position), et c'est encore un vecteur. Il en est de même pour l'accélération, correspondant à la dérivée seconde.

Dans un référentiel galiléen, l'accélération d'un point est proportionnelle à la force qui lui est appliquée. Une force est équivalente à un vecteur. La trajectoire d'une planète est connue par la force qui lui est appliquée à chaque instant. Cette force est la conséquence de la gravitation, essentiellement due au Soleil. Ce phénomène est décrit par la donnée du champ gravitationnel. Ce champ associe un vecteur proportionnel à la force de la gravitation à chaque point de l'espace.

Cette modélisation s'accommode plus difficilement de la relativité restreinte du fait que les changements de référentiels n'y dépendent pas linéairement de la vitesse, et elle ne concerne pas la relativité générale qui n'utilise pas d'espace euclidien (sauf pour des approximations). En physique quantique les coordonnées ne peuvent être celles d'une particule qu'en tenant compte du principe d'incertitude, et les forces sont dues à des échanges de particules.