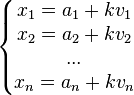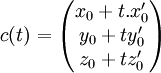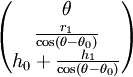Droite (mathématiques) - Définition
Pour les Anciens, la droite, en mathématiques et surtout en géométrie, était un objet allant de soi, si évident que l'on négligeait de préciser de quoi l'on parlait. L'un des premiers à formaliser la notion de droite fut le grec Euclide dans ses Éléments. Avec le développement du calcul algébrique et du calcul vectoriel, d'autres définitions vinrent s'ajouter. Mais c'est la naissance des géométries non euclidiennes qui a conduit à la découverte de nouveaux types de droites, et, par là-même, nous a forcés à éclaircir et approfondir ce concept.
Vision naïve
" La ligne droite est le plus court chemin pour aller d'un point à un autre ".
Cette définition simple suffit à bon nombre d'entre nous. Elle permet par exemple au jardinier de tracer ses lignes de semis : en tendant une corde entre deux piquets, il matérialise une ligne tirée au cordeau. C'est à un procédé analogue que recourt le bricoleur pour tracer une ligne de 5 mètres : il enduit une corde de craie, la tend entre deux points fixes puis, utilisant l'élasticité naturelle de cette corde, il l'éloigne du sol et la lâche soudainement. La corde reprend alors brutalement sa position initiale en déposant sur le sol une ligne de craie.
Voir aussi les définitions d'une demi-droite et d'un segment.
L'approche d'Euclide
Définition formelle
Dans ses éléments, Euclide définit les objets relevant de la géométrie (point, droite, plan, angle) et leur affecte un certain nombre de propriétés (postulats). À l'aide de ces éléments de base, il essaie de construire, par des démonstrations rigoureuses, l'ensemble des autres propriétés.
Pour Euclide :
- une ligne est une longueur sans largeur;
- et une ligne droite est une ligne également placée entre ses points.
Il part d'une droite finie qu'il définit comme un segment. Il a besoin d'un postulat pour la prolonger au-delà de ses extrémités, d'un autre pour en prouver l'existence (Par deux points distincts passe une droite) et d'un autre appelé le cinquième postulat d'Euclide pour traiter des positions relatives des droites ( Si une droite coupe deux autres droites, de telle façon que la somme des angles intérieurs du même côté soit plus petite que deux droits, ces droites, prolongées à l'infini, se rencontreront du côté où les angles sont plus petits que deux droits.) dont plusieurs versions équivalentes peuvent être données.
Applications
L'approche d'Euclide est féconde, elle permet de démontrer de nombreux théorèmes considérés comme élémentaire au regard des mathématiques au sens moderne du terme. On peut citer le théorème de Thalès, le théorème de Pythagore ou encore le problème de Napoléon.
Approche algébrique
Motivations
La définition axiomatique d'Euclide apparait trop pauvre pour résoudre plusieurs familles de problèmes. On peut citer historiquement ceux associés à la construction à la règle et au compas, par exemple la trisection de l'angle, la duplication du cube ou encore la construction d'un polygone régulier. Une approche algèbre est utilisée pour palier cette faiblesse. A l'aide de la notion de polynôme cyclotomique, Gauss réalise une percée majeure dans ce domaine en 1801 qu'il publie dans son livre Disquisitiones arithmeticae.
Les progrès de la physique engendrent une nouvelle branche des mathématiques, initialement appelée calcul infinitésimal et maintenant calcul différentiel. Elle obtient comme premier succès la compréhension de la mécanique céleste. Une fois encore, la modélisation d'Euclide est insuffisante pour formaliser convenablement ce domaine.
Géométrie vectorielle
Une nouvelle construction est alors proposée, elle se fonde sur des structures algébriques. Les groupes abéliens et les corps sont utilisées pour définir un espace vectoriel puis un espace affine.
En géométrie vectorielle, une droite est un sous-espace vectoriel de dimension 1.
Si v est un vecteur non nul, la droite vectorielle engendrée par v est l'ensemble des vecteurs w pour lesquels il existe un scalaire (un réel pour un espace vectoriel sur R) k tel que w = kv. On dit alors que les vecteurs v et w sont colinéaires.
Géométrie affine
En géométrie affine, une droite est un sous-espace affine de dimension 1. Si A est un point et v un vecteur non nul, la droite affine engendrée par A et v est l'ensemble des points M pour lesquels il existe un scalaire k tel que
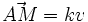
On peut aussi définir la droite passant par les points distincts A et B comme l'ensemble des barycentres des points A et B.
Applications
La notion de droite est alors largement généralisée. L'espace vectoriel peut être de cardinal fini comme pour les codes linéaires utilisés dans la théorie de l'information, ou en arithmétique. Une droite est alors un ensemble fini de points discrets. L'espace vectoriel peut être une extension de corps comme dans le cadre de la théorie de Galois, l'ensemble des nombres rationnels dans le corps des réels possède les propriétés géométrique d'une droite.
En analyse, et particulièrement en analyse fonctionnelle une droite est un ensemble de fonctions. Par exemple les primitives d'une fonction continue réelle de la variable réelle forment une droite.
Logique et géométrie
Motivation
L'approche algébrique permet d'enrichir très largement la géométrie et offre des réponses satisfaisantes à bon nombre de problèmes. En revanche une vielle conjecture reste ouverte : comment démontrer le cinquième postulat d'Euclide. Proclos l'exprime de la manière suivante: Dans un plan, par un point distinct d'une droite d, il existe une unique droite parallèle à d.
Déjà, les grecs savaient qu'une sphère semble pouvoir définir une géométrie, les droites seraient alors les grands cercles de la sphère. En revanche, la connexion entre une sphère et la définition d'une géométrie reste à cette époque or de portée.
Rôle de Hilbert
David Hilbert apporte un élément de réponse. La construction d'Euclide n'est pas entièrement rigoureuse. Il manque en effet, quinze axiomes pour bâtir les fondements d'un système logique à même de supporter la géométrie euclidienne. Une telle formalisation existe, on parle par exemple d'axiomes de Hilbert.
La réponse à la question que pose le cinquième postulat est donc de l'ordre de la logique. La base axiomatique d'Euclide constituée des quatre premiers postulats est trop faible pour garantir le cinquième.
Si l'approche de Hilbert permet de résoudre cette question, elle est peu opérationnelle pour bâtir la théorie de la géométrie euclidienne. On utilise en général la base axiomatique de Peano pour construire l'ensemble des entiers naturels puis les différentes structures algébriques utilisées. L'intérêt des travaux de Hilbert sur cette question est donc surtout de l'ordre de la logique et peu géométrique.
Géométries non euclidiennes
Bien avant de comprendre la dimension logique de la problématique et dans le courant du XIXe, sont nées d'autres géométries dans lesquelles la droite n'avait plus les mêmes propriétés que dans la géométrie euclidienne : les géométries non euclidiennes.
En géométrie projective, des droites parallèles se coupent en un point impropre et par deux points ne passe qu'une seule droite.
En géométrie hyperbolique, par un point donné, non situé sur une droite donnée, il passe au moins deux droites qui ne coupent pas la droite donnée.
En géométrie elliptique, deux droites sont toujours sécantes. Un exemple classique de géométrie elliptique est la géométrie sur une sphère où le plus court chemin pour aller d'un point à un autre est une partie d'un grand cercle. Une droite est alors définie comme un grand cercle. Deux droites distinctes se coupent alors en deux points diamétralement opposés qui n'en forment qu'un pour cette géométrie. On retrouve la propriété : par deux points distincts passe une seule droite.
De plus on peut aussi définir une droite comme un cercle de rayon infini.
Cette définition est incompatible avec celle issue de l'algèbre linéaire. Dans ce contexte, on parle en général de géodésique pour éviter une confusion.
Géométrie analytique
Si l'espace vectoriel est muni d'une base, ou l'espace affine d'un repère, la droite peut être caractérisée par des équations.
Espace affine de dimension 2
Une droite affine est l'ensemble des points M de coordonnées (x ; y) tels que
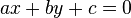
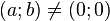
Dans cette famille de droites, on rencontre
- les droites d'équation y = mx associées à des fonctions linéaires de R dans R
- les droites d'équation y = mx + p associées à des fonctions affines de R dans R
- les droites d'équation x = p parallèles à l'axe des ordonnées
m représente la pente de la droite.
Faisceau de droites
Espace affine de dimension n
En dimension n, la droite passant par
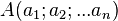
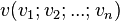
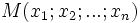
Ce système d'équations s'appelle un système d'équations paramétrées de la droite.
Cas particulier de l'espace (dimension 3), en :
- Coordonnées cartésiennes :
- Coordonnées polaires :