Relativité d'échelle - Définition

La théorie de la relativité d'échelle, développée par le physicien français Laurent Nottale, est une tentative visant à généraliser la théorie de la relativité générale. Pour cela, elle abandonne l'hypothèse classique de la différentiabilité de l'espace-temps, qui devient fractal. Un objet est alors caractérisé par un état " d'échelle " (assimilable à la résolution des instruments de mesure utilisés pour le décrire) qui ne peut être défini que relativement à un référentiel, à l'image des états de position et de mouvement.

La relativité d'échelle reste une théorie marginale et contestée.

Une généralisation de la relativité "générale"

L'idée moderne de la relativité remonte à Galilée, avec son fameux exposé sur les systèmes du monde, où il décrit le mouvement " qui est comme rien ", c'est-à-dire que le mouvement en tant que tel n'existe pas pour celui qui partage le même référentiel. La généralisation proposée par la relativité d'échelle est particulièrement naturelle lorsque l'on s'attache à décrire l'évolution de l'idée de relativité en fonction des propriétés du concept le plus fondamental de la physique : l'espace-temps.

Dans la relativité " galiléenne ", l'espace-temps est

1. continu
2. " lisse " (i.e. différentiable, et même infiniment différentiable - nous y reviendrons),
3. et " droit ", c'est-à-dire euclidien (i.e. Dans un espace où les droites parallèles ne se rejoignent jamais).

Il est alors possible de voir le travail d'Einstein comme la tentative de se soustraire de l'hypothèse de l'espace-temps euclidien ; les raisons qui l'ont amené là sont diverses, mais peuvent néanmoins se ramener à ça. Dans la relativité générale, l'espace-temps n'est pas supposé euclidien partout. En d'autres termes, l'espace-temps euclidien est un cas particulier (conforme à notre expérience ordinaire, certes, mais un cas particulier quand même) d'un espace plus général qui lui est courbe (et plus précisément riemannien). Et c'est précisément le but de la physique fondamentale que d'essayer de s'affranchir des conditions particulières pour atteindre les lois de la nature les plus générales.

Si l'on regarde l'équation d'Einstein aujourd'hui (cette équation représente en fait 16 équations différentielles du deuxième ordre couplées), on trouve des dérivées secondes. Implicitement, les coordonnées d'espace-temps sont donc considérées comme au moins deux fois différentiables.

En fait, Nottale n'est pas le premier à supposer les coordonnées d'espace-temps comme non différentiables: il suffit d'interpréter les équations dans le cadre des distributions.

Alors, toute la force de la relativité d'échelle résiderait précisément ici : elle consisterait à supprimer encore une hypothèse sur l'espace-temps, celle de la différentiabilité. L'espace-temps resterait continu. Cependant, il ne serait plus seulement courbe, mais aussi non différentiable, autrement dit fractal (conséquence du théorème de Lebesgue). C'est la force majeure de cette théorie face aux autres théories du tout : elle fait la seule hypothèse d'en supprimer une justement, et ce sur l'objet le plus fondamental de la physique : l'espace-temps. La relativité d'échelle est supposée englober donc par définition la relativité générale, puisqu'elle est supposée en être une généralisation. Ainsi, l'espace-temps courbe (riemannien) deviendrait lui aussi un cas particulier d'un espace-temps encore plus général.

Pour aller plus loin, il serait possible d'imaginer un espace-temps discontinu, mais il semble que ce ne soit pas (ou pas encore ?) utile pour comprendre les problèmes physiques auxquels nous sommes confrontés.

Justification conceptuelle

Un problème théorique que la relativité restreinte d'Einstein essayait de résoudre était l'apparition d'une constante, , dans les équations de Maxwell décrivant la propagation des ondes_électromagnétiques, dont la lumière. Le problème posé par cette constante ayant la dimension d'une vitesse est qu'elle semblait indépendante de la vitesse de l'observateur, et par conséquent n'obéissait pas à la loi additive de composition des vitesses v = v₁ + v₂.

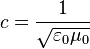
De la même façon, l'équation_de_Schrödinger fait apparaître une constante à partir de laquelle on peut dériver une distance fondamentale, la longueur de Planck , qui apparaît indépendante de la résolution à laquelle on l'observe, contrairement aux autres quantitiés assimilables à des longueurs.

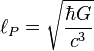
Tout comme l'existence d'une vitesse absolue c requiert l'écriture d'une loi de composition de vitesses qui laisse cette vitesse invariante (la Transformation_de_Lorentz), l'existence d'une longueur apparemment absolue suggère qu'il est nécessaire d'écrire les changements d'échelle d'une façon qui préserve cette longueur. La relativité d'échelle est principalement l'étude des conséquences d'une telle transformation.

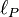
Calculs fondamentaux : exposé simplifié

En relativité générale, la composition des vitesses ne se réduit pas à une simple addition. Par exemple, vue d'une gare, la vitesse d'une balle dans un train n'est pas la somme de la vitesse du train et de la vitesse de la balle vue du train. Le calcul correct fait intervenir une composition des vitesse un peu plus compliqué mais calculable par la transformation de Lorentz, qui introduit une vitesse limite (celle de la lumière), pour laquelle v " + " c = c.

Avec la relativité d'échelle, la même chose se produit avec la composition des niveaux de " zoom ", qui ne se réduit pas à une simple addition (en échelle logarithmique). Autrement dit : si on passe d'une mesure d'un objet en centimètre à une mesure en millimètres par une multiplication par 10 (1 ordre de grandeur), et de la même mesure en millimètres à une mesure en micromètre par une multiplication par 1000 (3 ordres de grandeur), on ne passe pas de la mesure en centimètre à celle en micromètre par une multiplication par 10x1000 = 10 000 (1+3 = 4 ordres de grandeur). En supposant que la transformation de Lorentz se généralisait à la composition des échelles, Nottale a annoncé que cela impliquerait naturellement des tailles limites.

• une limite inférieure dans l'espace (on ne pourrait plus parler d’infiniment petit), qu'on peut identifier à la longueur de Planck
• une limite supérieure dans l'espace (on ne pourrait plus évoquer non plus d’infiniment grand), L, qui est la taille de l'Univers.
• une limite inférieure dans le temps, le mur de Planck.

Dans cette théorie, toutes ces limites sont aussi solides que le "mur de la vitesse de la lumière", vouloir parler d'un objet "au-delà" n'a pas plus de sens que parler d'un objet " plus rapide que c ". Notamment, regarder plus "tôt" dans le temps que le mur de Planck n'a pas non plus la moindre signification : le " big bang " est inaccessible.

Il est bien sûr possible de tenter un "zoom" supplémentaire, mais cela conduit à voir exactement la même chose (exactement comme se mettre dans un train encore plus rapide ne change pas la vitesse de la lumière observée).

"Assez loin" des échelles limites, on resterait dans le domaine " non-relativiste d'échelle ", où les lois classiques de composition des échelles s'appliquent : si un objet en mm est 10 fois plus gros que le même en cm, et si l'objet est 100 fois plus gros en cm qu'en mètre, alors il est, à une approximation impossible à prendre en défaut, 1000 fois plus gros en mm qu'en mètre. Selon le cas, c'est la mécanique quantique ou la relativité générale qui s'applique. Par contre, ces deux théories doivent devenir de plus en plus fausses au fur et à mesure qu'on se rapproche des échelles limites, les écarts prévisibles sont calculables, et c'est un point qui permettra de valider (ou au contraire infirmer) la théorie de la relativité d'échelle.

Conséquences

• L'espace aurait une nature fractale, (d’après Nottale, de dimension deux vers les petites échelles, ce qui lui fera par boutade considérer le monde physique comme similaire à un gros économiseur d'écran). Concrétement, cela signifie qu'un objet mesuré en millimètre est un peu différent du même objet mesuré en mètres (mais cf. infra).

• La relativité d'échelle explique la quantification et l'apparition de structures à différentes échelles (en dépit de la continuité de l'espace-temps), et ce, sans supposer une fluctuation initale ou une "force" spécifique. On retrouve cela en astronomie (astéroïdes, planètes et soleils ; systèmes solaires ; galaxies ; amas ; super-amas) et en physique des particules.

• la relativité d'échelle explique la conservation de la charge électrique comme liée à la symétrie d'échelle, et quantifiée en raison de l'existence de l'échelle limite de Planck.

• la densité d'énergie du vide dépend de la résolution, en 1/r⁶.

• Relativité générale et mécanique quantique, théories jusque-là incompatibles bien que donnant l’une comme l’autre des résultats valides, coexistent dans ce cadre unique et commun.

En effet, une des conséquences les plus étonnantes de cette théorie est qu’il existe des trajectoires qui varient indéfiniment suivant les changements d’échelles (il n’existe donc aucune échelle où ces trajectoires peuvent se ramener à une droite, comme c’est le cas en physique classique, autrement dit ces trajectoires sont des fractales). Ce résultat a deux conséquences importantes :

• Les mouvements apparemment aléatoires des particules de la physique quantique ne seraient en réalité que des mouvements suivant de telles trajectoires fractales (d’ou une possible unification de la physique quantique et de la relativité). Ce qui expliquerait aussi pourquoi le fait d’observer ces particules influe sur leur comportement, puisque une observation suppose forcément une échelle d’observation.

• Vu que le concept de dérivées mathématiques s’appuie justement sur le fait qu’une portion infiniment petite de courbe peut être assimilée à un segment de droite, l’existence de trajectoires fractales remet en cause l'application de ce concept à la physique réelle. Ainsi, aux échelles quantiques, les trajectoires des particules ne seraient pas différentiables, ce qui explique l’impossibilité de leur associer une vitesse au sens classique.

La mécanique quantique

Le plus remarquable, c'est que l'application des lois de la relativité d'échelle implique la quantification.

La mécanique quantique n'est ainsi pas abolie, elle apparait comme un simple cas particulier.

Cas des hautes énergies

Cependant, la relativité d'échelle implique que la mécanique quantique "standard" devient fausse aux très hautes énergies (supérieure à 100 GeV), car elle ne prend pas en compte les effets relativistes d'échelles qui deviennent sensible à ce niveau. En fait, la relativité d'échelle dans sa forme actuelle ne tient pas compte des modifications à faire dans le cas des hautes énergies. Par exemple, elle établit une correspondance entre les lois de Newton et l'équation de Schrödinger, mais en ce qui concerne les équations macroscopiques de la relativité restreinte et les équations de la mécanique quantique tenant compte des effets relativistes, Laurent Nottale y travaille encore.

À ce titre, on peut contester l'expression "généraliser la relativité générale" puisque la théorie n'est même pas encore accordée avec la relativité restreinte !

Autres branches de la science : une "mécanique quantique généralisée"

Laurent Nottale prétend appliquer le principe général de la relativité d'échelle à n'importe quel objet de science. Par exemple, il suggère une application à la biologie : aux grandes échelle de temps, un système chaotique finit par se comporter comme un système quantique, ce qui implique

• une hiérarchie d'organisation (dans l'espace des échelles) ; on observe ainsi des individus et des espèces, alors même que le répertoire génétique apparait (presque) continu.
• une structure fractale des arbres évolutifs (quantification dans le temps)
• des implications en morphogénèse et auto-organisation (dans l'espace et le temps)

Cette application innatendue a plutôt tendance à discréditer la thèse de Laurent Nottale. En effet, les lois mathématiques qu'il prétend trouver dans l'évolution de l'homme sont contestées par les paléontologues, qui pensent tout simplement que l'équipe de Nottale n'a choisi que les événements confirmant sa thèse et pire, considèrent qu'il s'agit d'un truquage en faveur de l'actuelle offensive néo-créationniste.

Nottale a par ailleurs proposé d'appliquer la relativité d'échelle à l'astrophysique.^[1] Il propose en particulier d'employer une "équation de Schrödinger généralisée" pour expliquer les positions des planètes. Contrairement à la loi de Titius-Bode, la loi qu'il obtient attribue plusieurs positions à la ceinture d'astéroïdes (Nottale assurant que les positions représentent bien la répartition massique). Autre caractéristique intéressante, sa loi prévoit l'existence possible de vulcanoïdes à 0,05 UA ou 0,18 UA du Soleil, quoique la distance la plus faible est peu probable aux yeux de Nottale (peu de chances pour un objet d'exister si près du Soleil). Son collègue G. Schumacher a donc participé aux recherches de vulcanoïdes, en vain. Mais comme le fait remarquer Nottale, puisque Einstein a parfaitement expliqué l'orbite de Mercure et que la relativité d'échelle reprend la relativité générale, l'objet doit nécessairement être 1000 fois moins massif que la Terre, donc peu aisé à détecter. On peut aussi noter que Nottale avait exagéré en qualifiant un objet si léger de planète (cela semblait un peu osé à l'époque, il est certain que la nouvelle définition ne donne aucune chance à un objet si léger d'obtenir ce titre).

Critiques de la relativité d'échelle

Certains estiment que la relativité d'échelle ne mérite même pas d'être appelée théorie, mais qu'elle n'est qu'un tas de semblants d'idées et de mots savants vidés de leur sens, et un jeu d'illusions pour briller auprès de personnes qui ne connaissent pas la physique de manière suffisamment approfondie, ou qui la connaissent mais ne font pas attention aux détails de ce que Nottale avance et/ou ceux-ci n'éveillent pas leur esprit critique (comme il a l'art de faire des séminaires superficiels cachant ses faiblesses devant ceux qui pourraient les détecter).

Les constestataires de la relativité d'échelle estiment donc qu'elle ne mérite pas plus d'attention que tant d'autres théories "révolutionnaires" absurdes, de gens qui pour beaucoup n'ont jamais étudié sérieusement la physique à la hauteur de ce qui serait nécessaire pour cela. Et ils regrettent que les médias ait eu le malheur de prendre ces divagations au sérieux.

Ils lui reprochent notamment

1. la fausse découverte de la non-différentiabilité, généralement englobée pour les champs usuels dans les calculs différentiels via la théorie des distributions, et monnaie courante en théorie quantique des champs; de sorte que celle de l'espace-temps (voire des notions plus radicales encore comme la disparition des points) est une évidence dès qu'on veut envisager une gravitation quantique.
2. l'invocation d'irrégularités de l'espace-temps dont les conséquences découleraient par la magie des dimensions fractales, sans souci de préciser la forme de ces irrégularités ni les lois qui les déterminent; cette notion n'étant au fond qu'un cas limite de courbure, de telles lois seraient finalement redondantes et donc en conflit avec l'équation d'Einstein de la relativité générale aux échelles macroscopiques où les effets quantiques sont absents.
3. la vacuité de sens du principe de relativité d'échelle à moins bien sûr de contredire l'évidence de définissabilité physique absolue des étalons de mesure.
4. l'invocation d'un groupe de dilatations "de Lorentz" dont une aberration parmi d'autres serait d'être, logiquement, différentiable, en contradiction, selon eux, avec l'hypothèse initiale de non-différentiabilité de l'espace-temps.
5. une prétention à inclure la mécanique quantique, alors que le principe de superposition quantique d'états engendre des effets fondamentalement originaux comme la violation des inégalités de Bell, dont il est évident qu'aucune théorie locale (respectant la relativité restreinte) et de type classique sur le plan métaphysique (donc, sans superposition quantique d'états) comme la RE, ne pourra jamais les reproduire.
6. une prétention à traiter simultanément des problèmes qui, selon eux, n'ont rien à voir entre eux : des problèmes d'astronomie dont rien n'indique l'influence fondamentale de lois inconnues comme celui de la formation de systèmes planétaires, et la physique des particules.

D’autres, de différentes spécialités scientifiques, adoptent une position plus nuancée voire favorable. Ils considèrent que le nombre d’articles publiés selon les règles de la communauté scientifique (et également dans la revue française de vulgarisation scientifique Pour la Science), est suffisamment important pour que le développement de cette théorie puisse être pris au sérieux.

(Cf. voir le lien externe critique)

voir aussi

• métaphysique :
  • relativité
• physique :
  • relativité générale et relativité restreinte
  • mécanique quantique
  • cosmologie
  • big bang
  • astronomie
  • exoplanètes
  • loi de Titius-Bode
• mathématiques :
  • fractal
  • théorie du chaos
  • différentielle et dérivée
  • lagrangien et hamiltonien
• Pseudo-science