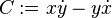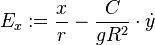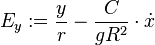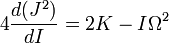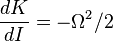Histoire du mouvement keplerien - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Avant Kepler - Le grand débat de la loi en 1/r^2 - La réception de la théorie de Kepler - Quelques démonstrations du mouvement keplerien

Introduction

La description du mouvement des planètes par Johannes Kepler à partir des tables établies par son maître Tycho Brahe est un tournant dans l'histoire des sciences qui prit naissance au début du XVII^e siècle. Malgré le retentissant procès de Galilée (qui doit abjurer sa conception copernicienne de l'univers le 21 juin 1632), le philosophe et mathématicien René Descartes verra, quelques années plus tard, le triomphe de sa méthode, d'après laquelle les sciences de la Nature reposent sur la méthode expérimentale.

Environ cinquante ans plus tard, la théorie sera écrite dans les Principia par Isaac Newton de fin 1684 à 1687, sous l'impulsion de son commanditaire et ami Edmond Halley. Ainsi naquit la mécanique céleste, ainsi que la mécanique rationnelle.

Le XVIII^e sera le siècle où l'on n'aura de cesse de clarifier cette théorie.

Avant Kepler

ébauche :

Ptolémée et l'équant

Copernic (1543) et la "révolution copernicienne" (cf Koyré)

Tycho Brahe, Uraniborg, et son "équivalence des systèmes"

Le grand débat de la loi en 1/r^2

ébauche :

Newton : les mesures de Richer et Picard (Guyane), de Halley (Sainte-Hélène), de Flamsteed (observatoire de Greenwich, les comètes)

Wallis, Hooke (1679), Halley-Wren-Hooke et le pari.

La réception de la théorie de Kepler

ébauche :

Galilée et les orbites circulaires, et les satellites médicéens.

Horrocks et le centre de "masse" ; Wallis et le centre de "gravité " du système Terre-Lune.

Quelques démonstrations du mouvement keplerien

Depuis la découverte des trois lois de kepler sur le mouvement des planètes, il y a de nombreuses démonstrations relatives au mouvement keplerien dont les plus anciennes virent le jour au XVII^e siècle. En voici quelques-unes.

Newton (1684)

1/. La première, celle de Newton en novembre 1684, est géométrique, le temps étant évalué par l'aire balayée (2ème loi de Kepler) : l'analyse en est faite dans l'Exégèse des Principia.

Hermann (1710)

2/. La plus simple (1710 & 1713) est celle de Jakob Hermann (1678-1733), élève de Jacques Bernoulli (1654-1705) : il écrit à Jean Bernoulli (1667-1748) : on remarque que l'hodographe est un cercle (notion de vecteur excentricité) : en calculant le produit scalaire e.r, on trouve l'ellipse et son péricentre. L'analyse est faite dans Invariant de Runge Lenz.

Laplace la reprendra dans son traité de « Mécanique Céleste ».

Que cela est vite dit dans notre langage moderne ! En réalité, la démonstration géométrique est la remarque classique sur le rôle des podaires dans le cas de champs centraux. Danjon remarque (avec Hamilton) que l'antipodaire de l'inverse d'un cercle est une conique : cela était enseigné encore au baccalauréat des années 1960 (Cf. LEBOSSÉ & EMERY, cours de mathématiques élémentaires).

Quant à Hermann, c'est un tour_de_force :

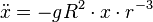
Il possède trois intégrales premières en coordonnées cartésiennes tirées de $\ddot{x} = -gR^2\cdot x \cdot r^{-3}$ et idem en y.

$C := x\dot{y} -y\dot{x}$
$E_x := \frac{x}{r} - \frac{C}{gR^2}\cdot \dot{y}$
$E_y := \frac{y}{r} - \frac{C}{gR^2}\cdot \dot{x}$

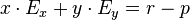
Éliminer la vitesse : on trouve $x \cdot E_x +y\cdot E_y = r- p$ : c'est une ellipse (Cf. conique, Kepler). Mais comment a-t-il trouvé les deux intégrales premières du vecteur excentricité ? par un raisonnement analytico-géométrique horriblement compliqué ! On sait aujourd'hui le faire par la théorie de la représentation linéaire des groupes (Moser et SO(4) : 1968). On trouvera sur ce sujet un article de Guichardet dans la Gazette des mathématiciens (été 2008).

Transmutation de la force par Newton

3/. La plus surprenante est celle de la Transmutation de la force (Newton, retrouvée par Goursat (1889)).

Keill (1708)

4/. La classique : Newton-Keill (en 1708) - Bernoulli (1719)

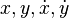
Le problème est plan, si la force est centrale. Le plan de phase est donc ( $x,y,\dot{x} , \dot{y}$ ). Les deux équations du PFD (principe fondamental de la dynamique) sont :

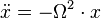
$\ddot{x} = - \Omega^2 \cdot x$

et la même en y. [Évidemment $Ω$ dépend de r!]. Cette notation est évidemment très réminiscente de celle de Hooke. Mais elle n'a rien à voir, sinon que la symétrie est centrale.

Choisir trois fonctions invariantes par rotation :

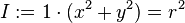
$I := 1 \cdot (x^2+ y^2) = r^2$ , strictement positif,
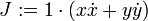
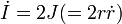
$J := 1 \cdot (x\dot{x} + y\dot{y})$ , de sorte que $\dot I = 2J (= 2r\dot{r})$ ,
$\ K := {v^2}/{2}$ , énergie cinétique.

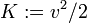
Remarquer cette particularité : r² est choisie comme variable, et non r. Et comme J est non-nulle, I va jouer le rôle d'une échelle de temps au moins sur une demi-période, du périgée à l'apogée.

Démontrer que le problème se réduit au système différentiel (S) :

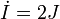
$\dot{I} = 2J$
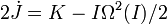
$2\dot{J} = K -I \Omega^2(I)/2$ (théorème du viriel !)
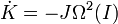
$\dot{K} = - J \Omega^2(I)$ (loi de Newton!)

Keill utilise alors l'échelle de temps I ; le système se réduit à :

$4\frac{d(J^2)}{dI} = 2K - I \Omega^2$
$\frac {dK}{dI} = - \Omega^2/2$

En éliminant Omega² (et quelle que soit sa valeur ! donc c'est vrai pour toute force centrale !)

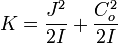
$K = \frac{J^2}{2I} + \frac{C_o^2}{2I}$ .

C'est un vrai tour de force : au début du XVIIIème, on vient de réécrire :

Emmy Noether connaissait-elle cette démonstration due à l'invariance par rotation ?

Puis, l'invariance temporelle donne la conservation de l'énergie :

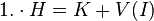
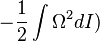
$1.\cdot H = K + V(I)$ , où V(I) est l'énergie potentielle relative à la force centrale (= $-\frac{1}{2}\int \Omega^2 dI)$

Ces deux ensembles de surfaces feuillettent l'espace (I, J, K) et leur intersection donne l'orbite du mouvement dans cet espace.

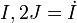
Éliminer K conduit à travailler dans le demi-plan ( $I, 2J = \dot{I}$ ), c'est-à-dire dans un plan de phase presque usuel (on joue avec r² plutôt qu'avec r) :

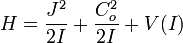
$H = \frac{J^2}{2I} + \frac{C_o^2}{2I} + V(I)$ ,

ce qui est l'équation de Leibniz (1689), mais en notation I = r². (Remarquer que tout résulte de cette circonstance, non évidente du temps où les vecteurs n'existaient pas) :

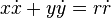
$x \dot{x} + y \dot{y} = r \dot{r}$ )

et pour finir, dt = dI/2J donne le mouvement sur cette orbite de phase et la primitive de 2J(I) donne l'action S(I) du problème.

Évidemment, actuellement, nous repasserions immédiatement en coordonnées (r et r'). Il n'empêche que voilà décrite la solution de Keill qui témoigne d'une virtuosité tombée dans l'oubli de l'Histoire. La suite est très classique et correspond à différents paramétrages dans le cas de Kepler. L'équation de Leibniz se réécrit dans ce cas :

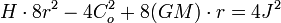
$H \cdot 8r^2 -4C_o^2 + 8(GM) \cdot r = 4J^2$

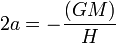
qui est une conique en J et r, ellipse si H est négatif de grand axe $2a = - \frac{(GM)}{H}$ :

Il est usuel alors de paramétrer via l'« anomalie excentrique » :

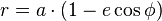
$r = a \cdot(1- e \cos{\phi})$ ,

et « miraculeusement » :

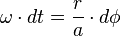
$\omega \cdot dt = \frac{r}{a} \cdot d\phi$ ,

qui s'intègre en donnant la fameuse équation de Kepler. En contrepartie l'équation en thêta est légèrement plus compliquée à intégrer (primitive de $\frac{1}{r}$ ) d'où :

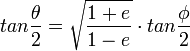
$tan \frac{\theta}{2} = \sqrt{\frac{1+e}{1-e}} \cdot tan \frac{\phi}{2}$ .

Clairaut (1741)

5/. La méthode de Clairaut (1741), reprise par Binet consiste à écrire l'équation de Leibniz à l'aide de u := 1/r :

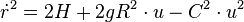
$\dot{r}^2 = 2H + 2gR^2 \cdot u - C^2 \cdot u^2$

et cette fois le paramétrage adéquat est :

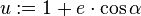
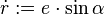
$u := 1+e\cdot \cos \alpha$ et $\dot{r}: = e\cdot \sin \alpha$

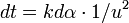
ce qui conduit au « miraculeux » $d θ = d α$ ! la trajectoire est donc une ellipse. Mais la deuxième intégration conduit à $dt = k d\alpha \cdot 1/u^2$ plus difficile à intégrer (mais tout à fait faisable !)

Lagrange (1778)

6/. La méthode de Lagrange est originale (1778) et n'utilise que la linéarité de F = m.a !

Partant de l'équation radiale de Leibniz (1689) :

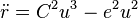
$\ddot{r} = C^2 u^3 - e^2u^2$

il pose comme nouvelle variable z = C²-r et trouve :

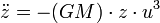
$\ddot{z} = -(GM) \cdot z \cdot u^3$ ,

identique aux deux équations de départ en x & y : donc il obtient z & x & y linéairement liés, ce qui est la définition d'une ellipse (Cf. conique, discussion). CQFD

Laplace (1798)

7/. Laplace, sans citer Lagrange, calcule, en force brutale, sans aucune intégrale première, l'équation en I = x² + y² du troisième ordre issue du système de Keill : d'où il tire

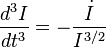
$\frac{d^3I}{dt^3} = - \frac{\dot I}{I^{3/2}}$

Laplace en tire cette fois quatre équations linéaires identiques : d/dt(r^3.Z") = - Z', avec Z = r, x, y, cste. D'où r = a x + by + c.cste : c'est une conique !

Hamilton (1846) et autres

8/. Soit une ellipse ; le foyer F et sa polaire, la directrice (D). Soit P le point courant de l'ellipse et PH sa projection sur la polaire. Le théorème de Newton-Hamilton donne immédiatement la force centrale F ~ r/PH^3 soit ~ 1/r².e³.

9/. Hamilton démontre aussi que pour toute mouvement sur une ellipse de paramètre Po, on obtient |a/\v|.Po = C^3/r^3. Donc si le mouvement est central de foyer F, |a/\v| = a.C/r d'où a ~ 1/r².

10/. Hamilton est aussi le promoteur du renouveau de la méthode de l'hodographe circulaire que Feynman reprendra à son compte dans ses « lectures on Physics »

11/. Hamilton va inspirer le Théorème de Siacci et puis Minkovski qui donnera beaucoup de propriétés des ovales : ceci donne encore une autre démonstration.

Goursat et régularisation dite de Levi-Civita

12/. Goursat (1889), Bohlin (1911), AKN {Arnold & Kozlov, Neishtadt} reprennent la méthode z→ sqrt(z) = U (complexe) et le changement d'échelle de temps (dit de Levi-Civita ou de Sundman) dt/dT = 4 |z| : quelques lignes de calcul donnent via le théorème de l'énergie cinétique :

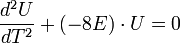
|dU/dT|² = 8 GM + 8 E |U|² ; soit par dérivation ${d^2U \over dT^2} +(-8E)\cdot U = 0$ , avec E négatif.

Donc U décrit une ellipse de Hooke et z =sqrt(U) l'ellipse de Kepler.

On aura reconnu en T(t), l'anomalie excentrique. Ce n'est donc qu'une des méthodes précédentes : mais cette méthode a des prolongements plus importants (Cf. théorème de Bertrand). Voir aussi plus bas.

Note : cette transformation du problème de Kepler en problème de Hooke est assez stupéfiante. Saari (p. 141) s'y attarde un peu plus qu'Arnold (BHHH) ; peut-être est-ce justifié ; voici :

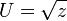
Le problème de régularisation se pose s'il y a collision, c'est-à-dire, C très voisin de zéro. Saari dit : la collision entraîne un changement brutal de 2Pi . Afin de garder la particule sur la droite sans singularité, il "suffit de penser" à garder l'arc -moitié ; soit de changer de jauge (de fonction inconnue): $\ U = \sqrt z$ et de variable (transmutation d'échelle de temps) dT = dt/r(t)(ATTENTION au facteur 4!)

La conservation de l'énergie s'écrit 2|U'|²-1 = Eo.r

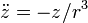
et l'équation du mouvement : $\ddot z = -z/r^3$ devient :

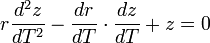
$r \frac{d^2z}{dT^2} - \frac{dr}{dT}\cdot \frac{dz}{dT} +z = 0$ ,

équation LINEAIRE sans le r^3 ! Elle conduit à :

U" -U/r [2|U'|²-1] =0

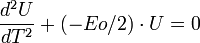
soit $\frac{d^2U}{dT^2}+ (-Eo/2)\cdot U = 0$ (équation de Hooke).

Le gros avantage de cette solution est qu'elle est stable-numérique : les solutions restent sur la même iso-énergie.

Kustaanheimo (1924-1997) et Stiefel (1909-1978) en 1964 utilisèrent enfin les quaternions pour transformer le problème de Kepler dans R^3 en celui de Hooke dans R^3, via R^4 ! (congrès d'Oberwolfach): ils leur a suffi de prendre la quatrième coordonnées x4 = cste : alors le quaternion U se déplaçait sur la sphère ; ceci mit en exergue la symétrie SO(4) et mieux SO(4,2) qui correspondait à la version spinorielle du problème de Kepler (liée à la solution en coordonnées paraboliques) et mettait en avant le vecteur excentricité. Immédiatement, le traitement des perturbations fut amélioré (Stiefel et Scheifel, 1971), mais aussi la quantification (méthode dite de Pauli (SO(4)), et surtout la quantification lagrangienne SO(4,2), aux orbitales "paraboliques" de Kleinert (1967-1998)(cf Kleinert 2006).

Saari donne des raisons topologiques à l'obstruction du passage de R^2 à R^3 et la nécessité de passer à R^4 (les quaternions) : la relation U^2 = z, ne pouvait se régulariser sur la sphère à cause du célèbre théorème du hérisson de Brouwer-Poincaré. Mais si on ne peut "peigner" S2 , on peut peigner S3 (et même S7 : octonions), ce qui avec les trois vecteurs tangents donne la fameuse matrice 4-4 de la transformation K-S : rappelons que le maître de Stiefel était Hopf lui-même qui dressa la carte de S3 vers S2 : il n'y a pas de hasard, la formation, cela sert ! (cf Oliver (2004)).

- Introduction - Avant Kepler - Le grand débat de la loi en 1/r^2 - La réception de la théorie de Kepler - Quelques démonstrations du mouvement keplerien

Le télescope James Webb, poussé à ses limites, découvre ces structures incroyablement anciennes 🔭

Le rôle surprenant de la grossesse contre la grippe A 🦠

Découverte d'une nouvelle espèce éteinte grâce à... un accélérateur de particules ⚛️

Une avancée prometteuse pour le déploiement des batteries sodium-ion 🔋

Voici comment et pourquoi le risque de cancer augmente... puis diminue avec l'âge 🧬

Le Soleil bientôt en "zone de combat": une période de turbulences extrêmes ☀️

Les rhumatismes plus douloureux par temps humide: vrai ou faux ? 🌧️

Ce nouveau type de moteur repousse les limites du vol supersonique ✈️

Poster sur les réseaux sociaux peut nuire à votre santé mentale 🧠

Une super-Terre entre Mars et Jupiter ? 🌎

Découverte impressionnante d'un fossile de crocodile géant 🐊

Cet accident en laboratoire pourrait transformer drastiquement la mémoire numérique ⚡

Un virage technologique révèle l'impact du diabète gestationnel 🩺

Insolite: ces loups butinent des fleurs ! Des grands carnivores pollinisateurs ? 🌼

Ce fin gilet robotisé soulage les tâches répétitives 🦾

Les équations d'Einstein invalidées ? 👀

Ce tatouage électronique se connecte à votre cerveau 🧠

Cette IA de Google prédit la météo mieux que jamais, et sur 15 jours ! 🌦️

Des plats au bœuf... sans bœuf ? 🥩

Ce moteur de recherche d'un nouveau genre bouscule nos habitudes 🔍

Pourquoi les cheveux bouclent-ils en fonction de la météo ? 🌦️

Découverte: d'autres univers plus propices à la vie que le notre 👽

Ces sons urbains qui minent notre santé mentale 🚗

La testostérone impacte-t-elle vraiment le désir sexuel des hommes ? 🔥

Des microalgues éliminent les métaux lourds: voici comment 🧪

Et voici un qubit mécanique ! 🖥️

Les lentilles de contact sont-elles vraiment sans danger ? 👁️

Dans la course à l'IA générative, Google lance son générateur de vidéos 🎥

Une zone oubliée du cerveau permet aux paralysés de marcher à nouveau 🧠

Cette astuce quotidienne ajoute 11 ans à votre vie 🕒

Révolutions, migrations des européens... les éruptions volcaniques ont influencé l'histoire 🌋

Soit l'énergie noire n'est pas constante, soit une seconde force inconnue est à l'œuvre... 🌀

Voici pourquoi l'alcool peut rendre agressif 🥂

Expérience inédite: ce laser projette une ombre visible 💥

Ce plat millénaire réduit significativement la graisse corporelle 🍽️

Les scientifiques trompés ? La Voie Lactée n'est PAS comme les autres galaxies 🔭

Pourquoi ce que pensent les autres de nous nous fait tant ruminer ? 🧠

De la vie découverte sur un échantillon de l'astéroïde Ryugu (oups) 👽

Des anomalies incompréhensibles de températures détectées simultanément presque partout sur Terre 🌡️

Cette planète, trop jeune pour exister, bouscule les lois de l'astronomie 🪐

Une montagne d'or découverte en Chine ⛏️

Cette simulation de l'Univers est totalement vertigineuse 🌀

Une pilule pourrait-elle imiter les bienfaits du yoga ? 🧘

Nous serions-nous trompés sur l'origine de l'écriture alphabétique ? ✍️

Voici pourquoi votre enfant triche et ce que cela révèle 🧠

Le Sahara verdit, et cela pourrait bien (re)changer notre climat 🌱

Neuralink: un bras robotique contrôlé par la pensée 🦾

Ces fossiles humains à grands crânes seraient-ils une espèce jusqu'alors inconnue ? 💀

L'étonnant impact du froid sur notre sommeil ❄️

Une base cachée de missiles nucléaires repérée par erreur sous la calotte glacière ☢️

Page générée en 0.210 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise