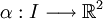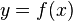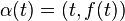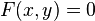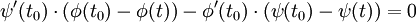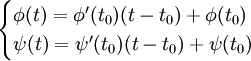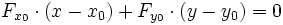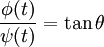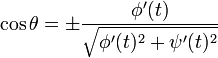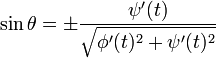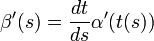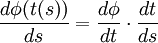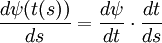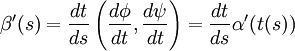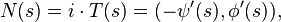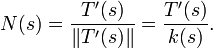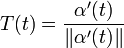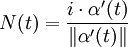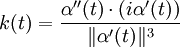Courbe plane - Définition
En géométrie, une courbe plane est une courbe qui est entièrement contenue dans un (unique) plan, et qui est identifiable à une fonction continue :
où I est un intervalle de l'ensemble

L'image d'une courbe est aussi appelée support de la courbe. Parfois, on utilise aussi l'expression courbe pour indiquer le support d'une courbe. Une courbe sur un espace euclidien de dimension supérieure à 2 est dite plane si son support est contenu dans un plan lui-même contenu dans l'espace euclidien dans lequel elle est définie.
Une courbe plane est dite simple si elle ne se recoupe pas, autrement dit, si
-
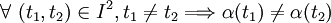
Représentations
Représentation par une forme cartésienne explicite
Une manière de représenter une courbe plane est l'équation :
telle qu'à chaque point x corresponde un point y, et de façon à ce que chaque point du plan xy : (x,y) représente le support de la courbe. Une courbe de ce type est également nommée graphique en référence au graphique d'une fonction réelle ; en effet, la représentation peut aussi s'écrire :
c'est-à-dire comme fonction d'une variable indépendante. Cette représentation a de nombreuses limites géométriques, du fait que très souvent, une courbe a une description très complexe sous cette forme, qui n'est donc pas adaptée à l'étude des propriétés géométriques.
Représentation par une forme cartésienne implicite
Une courbe peut également être représentée sous la forme :
c'est-à-dire comme fonction de deux variables indépendantes. Cette représentation est, selon certains points de vue, meilleure que la représentation explicite ; cependant, on peut rencontrer des problèmes quand il faut expliciter l'une des deux variables en fonction de l'autre : souvent, c'est très compliqué, quand ce n'est pas impossible.
Représentation paramétrée
La meilleure représentation est sans aucun doute la représentation paramétrée, du type :
-
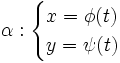
où
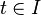
La condition de continuité ne suffit pas pour représenter et étudier les courbes vues comme objets filiformes à une dimension avec les caractéristiques de régularité voulues. La condition supplémentaire est que la courbe plane soit différentiable sur I.
Une courbe plane paramétrée α(t) = (φ(t),ψ(t)) est dite différentiable en tout point si les fonctions φ(t) et ψ(t) ont des dérivées continues en tout point.
On dit qu'une courbe plane paramétrée est régulière en un point t0 (ou que t0 est un point régulier pour cette courbe) si
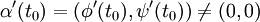
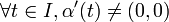
Un point t0 tel que α'(t0) = (0,0) est appelé point singulier pour la courbe.
Tangente
La régularité de la courbe permet de définir la droite tangente à la courbe. Soient α(t) une courbe différentiable et P0 = α(t0) un point régulier. On peut définir la tangente à la courbe en ce point comme étant la droite passant par P0 et parallèle au vecteur α'(t0) = (φ'(t0),ψ'(t0)).
La tangente a une équation cartésienne au point t0 :
et pour équations paramétrées :
Dans le cas d'une courbe représentée explicitement par une équation y = f(x), la tangente au point (x0,y0) est donnée par la relation :
-
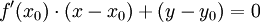
Dans le cas d'une courbe représentée par une équation implicite F(x,y) = 0, la tangente au point (x0,y0) est donnée par la relation :
où
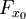
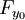
Normale
La régularité de la courbe permet de définir la droite normale à la courbe au point t0, d'équation cartésienne :
-
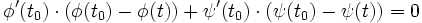
Cette équation devient, avec les mêmes notations que dans le paragraphe précédent :
- Pour une représentation explicite :
-
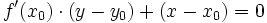
- Pour une représentation implicite :
-
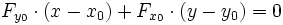
Cosinus directeurs
D'après la définition même de la dérivée, on obtient :
ce qui, d'un point de vue géométrique, représente la pente de la droite tangente à la courbe, autrement dit la tangente (au sens trigonométrique du terme) de l'angle que cette tangente forme avec l'axe horizontal (l'axe des 'x'). De cette relation, on peut extraire les cosinus directeurs de la tangente à la courbe :
Reparamétrage
Soient
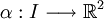
telle que pour tout
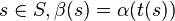
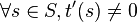
On vérifie alors le théorème suivant : si
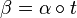
- Démonstration
- Si α(t) = (φ(t),ψ(t)) alors β(s) = (φ(t(s)),ψ(t(s))) et d'après les théorèmes de dérivation des fonctions composées, on a :
- et ainsi on obtient :
Longueur d'une courbe
Longueur d'un arc paramétré
Soient α(t) = (φ(t),ψ(t)) une courbe différentiable sur I, et
![[a,b]\subseteq I](https://static.techno-science.net/illustration/Definitions/autres/0/0c821dc116e0e2afe7e0856071a2479e_c8bdcb6b5aa0f01abde4fd9839edc669.png)
-
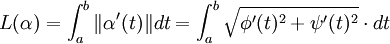
Si de plus β(s) est un reparamétrage de la courbe, alors :
-
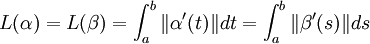
Longueur et forme cartésienne explicite
Si la courbe est représentée sous forme cartésienne explicite y = f(x) alors, comme
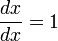
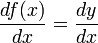
-
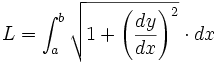
Paramétrage avec les coordonnées polaires planes
Une forme de paramétrage qui revêt une importance notable dans l'étude des mathématiques, de la géométrie et dans de nombreux domaines d'application des mathématiques, est celle des coordonnées polaires planes. Étant donnée une courbe paramétrée en coordonnées polaires par la forme cartésienne r = r(θ), avec c ≤ θ ≤ d, et par la forme paramétrée :
-
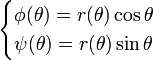
Alors ses dérivées sont :
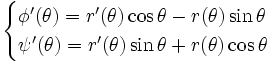
et donc la longueur de l'arc est :
-
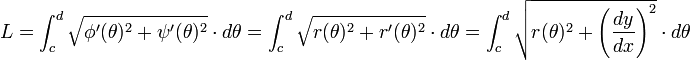
Abscisse curviligne
On définit l'abscisse curviligne ou paramètre longueur d'arc comme étant le reparamétrage particulier obtenu en fixant la borne inférieure d'intégration a, de façon à ce que l'intégrale
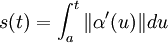
étant donné que
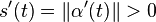
On démontre ensuite que le vecteur tangent est unitaire :
-
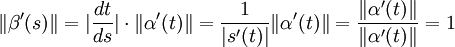
Courbure
Soit β(s) une courbe paramétrée selon l'abscisse curviligne et β'(s) son vecteur tangent unitaire. Considérons la fonction
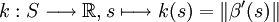
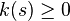
Si la courbe est représentée explicitement, sa courbure est :
-
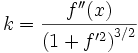
En revanche, pour une courbe représentée par une équation implicite, la courbure est évaluée par :
-
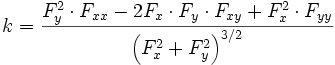
Formules de Frenet
Une courbe (suffisamment régulière) de l'espace possède, en tous ses points, un système de référence, dit trièdre de Frenet, donné par un triplet de vecteurs tangent, normal e binormal. Une telle courbe est plane si et seulement si le vecteur binormal est toujours nul.
Soit β(s) = (φ(s),ψ(s)) une courbe paramétrée selon l'abscisse curviligne. Le vecteur unitaire tangent est déterminé par :
- T(s) = β'(s) = (φ'(s),ψ'(s)).
Le vecteur unitaire normal est déterminé par :
où i est le nombre complexe tel que i2 = − 1. Grâce à la définition de la courbure, on peut donner une autre forme au vecteur unitaire normal :
On démontre que le vecteur T' est orthogonal à T et donc parallèle à N.
Finalement, les formules di Frenet et la courbure pour une courbe plane, quel que soit son paramétrage α(t) = (φ(t),ψ(t)), sont :
Exemples de courbes planes
Courbes planes classiques
- La droite
- Le cercle
- Le cercle unité
- les cissoïdes :
- La cissoïde de Dioclès
- La cissoïde de Sluze
- Les coniques :
- l'ellipse
- la parabole
- l'hyperbole
- les courbes cycloïdales :
- la cycloïde
- l'épicycloïde
- l'hypocycloïde
- la cardioïde
- la néphroïde
- l'astroïde
- la deltoïde
- Les courbes isochrones :
- L'isochrone de Huygens
- L'isochrone de Leibniz
- L'isochrone paracentrique
- L'isochrone de Varignon
- les lemniscates :
- Le lemniscate de Bernoulli
- Le lemniscate de Gerono
- Le lemniscate de Booth
- Les spirales :
- La spirale d'Archimède
- La spirale hyperbolique
- La spirale logarithmique
- La spirale de Fermat
- La spirale de Nielsen
- La spirale de Cotes
- La spirale de Galilée
- la sinusoïde
- l'exponentielle
- l' atriphtaloïde
- la chaînette
- Le folium de Descartes
- l' hélice
- les conchoïdes
- le limaçon de Pascal
- La lituus
- Les pétales de rose
- La strophoïde
- La superellipse
- la tractrice
- La trisectrice de Maclaurin
- la courbe du chien
- les courbes enveloppes
- les courbes développantes
Constructions
- La courbe du dragon
- Le flocon de Koch
- Les courbes de Bézier
- Les splines
Courbes analytiques
- Courbe fermée
- Courbe rectifiable
- Courbe de Jordan
- Courbe de Peano
- Courbe de Sierpinski
Courbes algébriques
Une courbe algébrique est une variété algébrique de dimension 1, généralement exprimée sous la forme d'un polynôme de degré divers. Des exemples incluent :
- Les droites projectives
- Les courbes quadriques, autre nom des coniques, de degré 2
- Les courbes cubiques, de degré 3
- La cubique d'Agnesi
- Les courbes quartiques, de degré 4
- La courbe de Klein
- Les courbes quintiques, de degré 5
- La quintique de l'Hospital
- Les courbes sextiques, de degré 6
- Les courbes elliptiques
- Les courbes hyperelliptiques
- Les courbes modulaires
- Les courbes de Fermat