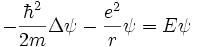Atome d'hydrogène - Définition
- Pour consulter l'article plus général, voir atome.
L'atome d'hydrogène est l'atome le plus simple qui existe : il n'est composé que d'un proton et d'un électron. C'est le premier élément de la classification périodique.
Comprendre la théorie quantique de cet atome fut très important car il est le modèle sous-jacent de la théorie des atomes à N électrons; cela a aussi permis de valider successivement les théories de la physique quantique au fur et à mesure des progrès accomplis : d'abord l'ancienne théorie des quanta (cf. atome de Bohr), puis la mécanique quantique non relativiste (de Schrodinger), la mécanique quantique relativiste de Dirac, et enfin la théorie quantique des champs.
L'article ici présente les résultats de la théorie de Schrodinger : on considère donc acquis les résultats établis dans l'article atome de Bohr.
La théorie montre que, aux niveaux d'énergie En, sont associées 2n² orbitales. Ces orbitales sont décrites d'abord en détail pour la couche K (n=1, niveau dit fondamental); puis pour les couches L, M, voir orbitale de l'atome d'hydrogène
Note d'histoire : la période 1913-1925
L'étude du spectre de l'atome d'hydrogène avait déjà été effectuée de façon empirique par Balmer (1825-1898) au 19ème siècle.La mise en évidence de régularités dans le spectre - inexplicable par la théorie classique - fut longtemps une énigme.
- Puis la théorie de l'atome de Bohr(1913) ne pût pas expliquer le cas du moment cinétique nul. Par ailleurs, elle introduit une hypothèse ad hoc (quantification des orbites permises) inconciliable avec la théorie classique.*Surtout, on ne pouvait pas expliquer la spectroscopie des autres éléments, même de l'hélium, élément avec seulement DEUX électrons, bien que très vite, Bohr put expliquer la spectroscopie des ions He+ et Li++.
On savait qu'il existait, en spectroscopie, deux "sortes" d'hélium, mais l'énigme restait entière, et ne relevait pas du tout de l'astuce de l' hydrogène de Pickering ( cf atome de Bohr).
- L'apport de Sommerfeld en introduisant la théorie des ellipses de Rutherford permit bien d'introduire la notion de moment cinétique orbital, mais fut une impasse (provisoire).
- L'effet Zeeman, puis la théorie du moment cinétique quantique de Pauli venait contredire la théorie de Bohr. On ne pouvait pas expliquer la structure du spectre de l'atome d'hydrogène pour les raies très voisines, c’est-à-dire la structure fine.
- Pauli dès 1924 comprend la notion de spin de l'électron et introduit son incompréhensible principe d'exclusion de Pauli qui ne deviendra un théorème que dans la théorie quantique relativiste ;
- Grâce à ce principe et à l'Aufbau-ensatz (hypothèse de remplissage), la classification périodique commence à recevoir un statut plus "théorique".
Erwin Schrodinger publia une équation en janvier 1926 :
l'équation de Schrodinger
|
L'observable position
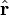
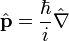
Cette théorie avait pour fondement la notion mathématique des opérateurs linéaires dits observables (ie opérateur hermitien, complet) dans un espace vectoriel abstrait, muni de la structure d'espace de Hilbert;
de ce fait la théorie fut autrefois appelée : mécanique des matrices, inventée dès 1925 par Heisenberg et utilisée brillamment par Pauli pour trouver le spectre de l'hydrogène, dès 1925. Mais cette théorie de Pauli était trop en avance sur son temps.
- Schrodinger, dès 1926, montra que la théorie d'Heisenberg se réduisait à la sienne, et que sa théorie donnait, gràce à sa fameuse fonction d'onde Ψ(r,t),(encore imcomprise en 1926), TOUT sur l'état stationnaire de l'électron "autour du noyau", SANS TRAJECTOIRE (mais ceci ne fut compris qu'en 1929/1930 gràce à Born, Jordan et Von Neumann, puis Dirac).
- On se doit de noter ici l'absence de deux Grands Physiciens : Einstein et Bohr. Leur correspondance de 1926 à 1935 montrent qu'ils auraient tellement voulu que cette théorie soit pleinement compréhensible !
- Ceci étant, la Théorie de Pauli de l'atome d'hydrogène était pourtant vraiment la plus profonde, et cela est maintenant reconnu par tous les récents ouvrages (environ depuis 1964).
_Complètement acquise au XXIème siècle, via l'invariant de Runge Lenz quantique, la théorie de Pauli est ENFIN en pleine lumière, après plus de quatre-vingt ans! C'est dire que le progrès de l'interdisciplinarité (ici théorie mathématique de l'intégrabilité et symétrie en chimie) est lent.
Ainsi, Schrodinger pût donc déduire en 1926 le spectre de l'hydrogène à partir des valeurs propres de l'opérateur linéaire
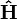
- ses valeurs propres redonnaient exactement les valeurs de l'énergie trouvées dans l'ancienne théorie de l'atome de Bohr (1913),
mais il obtînt bien plus :
- les fonctions d'onde de chaque valeur propre, c’est-à-dire la probabilité de trouver l'électron à telle ou telle position en régime stationnaire.(cf orbitale de l'atome d'hydrogène).
Ceci dit, résoudre l'équation précédente est un effort mathématique très difficile pour tout physicien non rompu à la pratique des équations aux dérivées partielles. Mais plus encore, la disparition de la notion de trajectoire et le concept d'électronde remplaçant celui d'un électron fut TRÈS difficile à admettre (cf mécanique quantique).C'est CELA qui explique la "réticence" d'Einstein. Et c'est une heureuse chance que l'équation pour l'atome d'hydrogène fût intégrable !
État fondamental
En fait dans le cas de l'atome d'hydrogène, on peut trouver la solution de l'état fondamental (c'est-à-dire de plus basse énergie) rigoureusement, en s'aidant uniquement du principe d'incertitude d'Heisenberg. C'est une façon très élégante de procéder, sans beaucoup de mathématiques.
En effet, très vite, (en 1929), Werner Heisenberg fait comprendre un des points clefs de la mécanique quantique : Les grandeurs physiques ne sont plus des fonctions
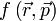
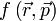
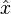
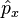
|
Alors, dans le cas d'égalité stricte - on dit que l'inégalité a été saturée à sa limite - la saturation des inégalités d'Heisenberg donne un moyen rigoureux de calculer la fonction d'onde,Ψ1s(x,y,z), de l'état fondamental de l'atome d'hydrogène.
Ce problème de valeur propre et de vecteur propre est donc résolu, dans l'article Saturation des inégalités d'Heisenberg, pour la plus basse énergie (cf. atome de Bohr) ; et cela donne:
|
|
N' étant la constante, réelle, dite de normalisation de la probabilité.
Vérification
On va se contenter ici de vérifier que ceci est vrai en insérant directement cette solution dans l'équation de Schrodinger.
Premièrement, dans cette équation, la variable temps se sépare immédiatement :
dans ce cas dit stationnaire, cela amène à trouver les valeurs propres de l'opérateur linéaire H dans l'espace L2 des fonctions des trois variables ƒ(x, y, z) à valeur complexe, de carré sommable :
-
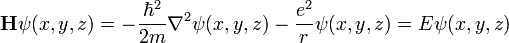
Or, dans ce cas, cette fonction uniquement de r a pour Laplacien, la valeur usuelle
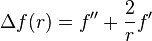
De plus, on se sert évidemment des unités atomiques, qui a été introduit à cet usage. Cela revient à faire
![[ \hbar = m = e^2 = 1]](https://static.techno-science.net/illustration/Definitions/autres/2/22cdd9d7aee4dde71b88888fa61fbd4b_a378cfff09031d9e8ecfa8a43f96d48f.png)
- ƒ = ƒ, ƒ' = - ƒ ;
donc il s'agit de vérifier si :
- -1/2·(ƒ + 2/r·(-ƒ)) + 1/r·ƒ = -1/2·ƒ
qui est vrai.
Densité de probabilité de présence
0n en déduit aussitôt la probabilité dp de trouver l'électron à une distance du noyau comprise entre r et r+dr : elle est donnée par dp = P(r)·dr :
-
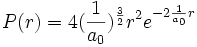
Sur le graphique de la densité de probabilité, la distance au noyau est donnée en multiple du premier rayon de Bohr, on voit immédiatement que la probabilité est maximale au premier rayon de Bohr :
- Le graphique va bientôt être réctifié. - (en particulier, il faut enlever ce malencontreux 4 qui perturbe la lecture, merci d'avance). (il est mieux représenté dans atome)
Orbitale 1s
Cette solution s'appelle en chimie l'orbitale 1s.
On pourra vérifier le théorème du viriel :
- moyenne de 1/r = 1/a0
et le théorème d'Ehrenfest :
- moyenne de 1/r² = 2/a²
La moyenne de r n'est pas a, mais (3/2)·a ; [de manière générale, l'inverse de la moyenne n'est pas la moyenne de l'inverse ].
Et la moyenne de r² vaut : 3a², donc la variance de r vaut (3-9/4)·a² = 0,75·a² ; soit un écart-type = 0,866·a², ce qui est très grand.
L'électronde est dite délocalisée dans un espace, qui malgré tout reste de volume fini, au sens physique : au bout de 3a, la probabilité de détecter l'électronde est très faible (on parle d'orbitale sphérique), typiquement en chimie quantique, on convient formellement de tracer la méridienne de la surface qui englobe en gros 98 % de chance d'y trouver l'électron :
- ici r = 3/2 + 1,732 ~ 3,2·a. Ceci est très conventionnel.
Note : espace des impulsions
L'opérateur impulsion a évidemment une moyenne nulle (symétrie sphérique), mais l'opérateur P² vaut 2m·Ec, dont la valeur moyenne est par le théorème du viriel
- <P²> = -2m·Ec, soit en unités atomiques +2·1/2 = 1.
Donc la variance de P vaut
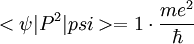
On retrouve bien (heureusement!) ce dont on était parti dans l'article Saturation des inégalités d'Heisenberg.
Mais on peut aller un peu plus loin [ ne jamais perdre de vue que l'espace des impulsions joue un rôle égal à celui des positions, bien qu'il soit moins étudié en chimie] :
Remarque : représentation dite des impulsions
- La transformée de Fourier de
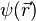
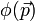
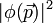
- En fait ce n'est pas une particule, ce n'est pas une onde, c'est une entité nouvelle, la " particlonde ", qui ne satisfait plus les équations de la mécanique classique (dans la version dite d'Hamilton), ni l'équation des ondes de l'optique, ni l'équation de la diffusion, mais cette drôle d'équation, l'équation de Schrodinger qui ne se laisse appréhender concrètement que dans la vision lagrangienne de Dirac et Feynman(on parle d'intégrale de chemins ( et parfois l'équation de Schrodinger est appelée équation de cheminement)). Si bien que l'énergie cinétique n'est pas du tout négligeable, puisqu'égale à 50% de l'énergie potentielle en module.
Remarque : Kleinert, élève de Feynman, a réussi à donner l'interprétation du "cheminement" dans le cas de l'atome d'hydrogène, mais cela reste une prouesse. En ce sens , pour les chimistes, le seul vrai progrès notable depuis Hartree-Fock et Clementi a été (pour l'atome à N électrons), la notion de densité fonctionnelle de Kohn ( Nobel de chimie 1998).
Conclusion
Il faut garder en mémoire toujours ces deux aspects, le couple [Ψ(r),Φ(p)], pour bien comprendre l'aspect non statique, mais stationnaire de cette délocalisation de l'électronde. Beaucoup de livres proposent comme règle empirique : si l'électronde est localisé dans une région de l'ordre de r = a, lui donner une énergie cinétique de l'ordre de
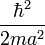
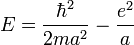
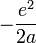
-
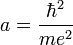
C'est une façon simple et élégante d'introduire les OdG ( ordre de grandeur)de l'atome, souvent reprise dans les bons ouvrages.
États stationnaires des couches L, M
ébauche
Les autres valeurs propres et les autres états propres sont plus difficiles à calculer.On se contentera ici de leur description. Pour la démonstration, voir Théorie de Schrodinger de l'atome d'hydrogène.
Niveaux d'énergie
Le spectre de l'hydrogène est connu avec une précision exceptionnelle ; de même en est-il pour l'ion He+, et l'ion Li++, etc. que l'on forme assez facilement par spalliation. Mais il faudra tenir compte de la variation de la masse réduite (cf. atome de Bohr, hydrogène de Pickering ) ; et bien sûr du changement de e² en Ze², Z étant la charge du noyau. Le tracé expérimental de -E(Z, n).n²/Z², corrigé de la masse réduite et de légers effets relativistes (qui varient comme Z²) est assez fascinant de platitude, alors qu'on peut aller jusqu'à des n de l'ordre de 80, et Z de l'ordre de 15.
- D'autre part, pour l'atome ou ion à N électrons, on pourra comparer les niveaux d'énergie E(N, Z,n, l,m)/Z² pour le même N : ils sont assez analogues bien que le problème soit très différent (cf. atome à N électrons).
- Enfin signalons le cas des atomes hydrogénoïdes ( les alcalins ou ions qui y correspondent : le dernier électron, surtout s'il est excité, présente un spectre très analogue à celui de l'hydrogène, car les électrons des couches inférieures de symétrie sphèrique, du fait du théorème de Gauss, écrantent la charge Z du noyau, ne laissant apparaître, surtout pour les orbitales de l= n-1, m=0, qu'une charge écrantée Z(effectif)= Z-(N-1) apparemment ponctuelle.
- Rappel : pour des Z élevés, les électrons dits de couche profonde de l'atome à N électrons, par exemple les électrons 1s, seront à des énergies très basses ( -Z².13.6 eV, soit pour Z =10, des énergies déjà 100 fois 13.6 eV ): sachant que la chimie ne porte que sur des énergie au plus de qq dizaines d'eV, il apparaît déjà clair que ces électrons ne joueront aucun rôle en chimie. Seuls les électrons de valence interviendront ; et c'est bien là l'essentiel de ce que dit la classification périodique.
Allure des orbitales
Il est extrèmement important de se représenter les orbitales
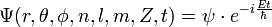
Ne pas oublier aussi que [même pour les états (ns)], l'énergie cinétique de l'électronde-délocalisé est la moitié de l'énergie électrostatique : il convient de se représenter mentalement le couple [densité électronique, phase électronique], couple qui sera si important en chimie quantique pour apparier les électrons : dans l'équation de Schrodinger sur le corps des complexes, on ne répètera jamais assez qu'il y a DEUX équations réelles couplées : l'une considère le module de psi, soit a, l'autre la phase, soit S/

|
on aura:
|
et
|
- La première équation s'appelle la conservation de la densité électronique avec un courant de probabilité .
- La deuxième équation s'appelle équation de l'eikonale de Schrodinger.
Et donc tout cela "bouge" de façon stationnaire, via des tirages au sort de probabilités stationnaires.
- Les calculs (assez ardus ?) montrent que les fonctions d'onde s'expriment en coordonnées polaires sous la forme :
|
- n est le nombre quantique principal
- l est le nombre quantique azimutal
- m est le nombre quantique magnétique
- k : = n-l+1 est le nombre de zéros de la fonction S(r)= r.R(r) et s'appelle nombre quantique radial.
les fonctions
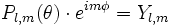
Dans ce cas, chaque fonction d'onde individuellement donnera une vision simplifiée : le courant
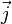
D'autre part, il n'y a pas de "gelée électronique" représentant peu ou prou l'électronde délocalisé, même s'il est éminemment utile de tracer les orbitales chimiques.
Enfin, l'équation de l'eikonale se réduit simplement à ce qu'on appelle l'équation de Schrodinger stationnaire:
|
Lors de l'hybridation des orbitales, il conviendra de reprendre ces calculs : la linéarité sur le corps des complexes produit des termes d'interférence constructive et destructive, si caractéristiques de la chimie quantique.[une orbitale hybridée est superbement représentée dans atome ]. .
Réprésentation des harmoniques sphériques
- La représentation des harmonique sphérique est excellemment faite dans ce lien.
On pourrait essayer une réprésentation(cf. White 1935), si possible de façon dynamique !
- Une fois bien saisie la forme des Ylm et leur symétrie, la deuxième chose dont on doit se souvenir est que en gros la théorie de Bohr est satisfaite via les R(r).
variance de la position
On peut rappeler plus précisément :
moyenne de 1/r = Z/n², indépendante de l, c'est la dégénérescence "accidentelle" déjà vue.
variance(1/r) = Z²/n? [
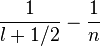
Donc la variance relative est grande pour les états s , mais pour les états de Rydberg décroît comme ~ 1/2n², soit pour n = 60, inférieure à 2.10^(-4) et les Y(n-1, m) donnent pour une "bonne combinaison", une bonne localisation en théta = 90° et en phi(t) : en gros, le paquet d'ondes qui représente l'électronde-délocalisée n'est pas si délocalisé que cela, et on retrouve assez bien l'image classique de Bohr; mais cela ne dure pas: le paquet d'ondes s'étale (sur un espace torique).
Ceci dit :
moyenne de r : 1/2Z . [3n²-l(l+1) ] : un électron s ( l=0) est beaucoup plus "loin" et plus "proche" du noyau qu'un électron de Rydberg (l = n-1).Cela n' a rien de paradoxal si l'on pense à une comète, et en mécanique quantique à la délocalisation de l'électectronde.D'ailleurs,
moyenne de r² : 1/2Z² . n²[5n²+1-3l(l+1)]
On voit donc que la variance d'un électron s est n?/4, la variance relative est 1/9 ~11% : c'est énorme, compte-tenu de la taille de r(n) = n².r(1) : Si l'on imagine cela pour toutes les planètes, il y aurait un gros grabuge dans le système solaire. Dans l'atome, il faut bien s'imaginer que si n= 3 ou n= 4, un électron s pénètre beaucoup dans les couches profondes (il correspondrait à une comète en mécanique céleste), et va donc interagir avec celles-ci : cette question devra être examinée soigneusement dans le cas de l'atome à N électrons.
Au contraire, pour un électronde de Rydberg :
variance(r) = 1/4Z² .[n²(n+2) - l²(l+1)²] soit avec l= n-1: [2n³+n] donc une variance relative en ~ 1/2n.
- Remarque : la valeur moyenne de 1/r³ se trouve astucieusement reliée à celle de 1/r² : Z/r² - l(l+1)/r³ =0, en moyenne.
- Remarque : les relations de Pasternak donnent toutes les valeurs moyennes de r^k, k entier.
Note: Couche K, rappel ===
Elle ne comprend qu'un état de symétrie sphérique, l'état fondamental, déjà amplement décrit.
Couche L
elle comprend une orbitale (2s) sphérique et 3 orbitales (2p) en "larmes d'eau": voir harmonique sphérique
- orbitales 2p : k=1
figure ici
- orbitales 2s : k=0
à symétrie sphérique figure ici
Couche M
elle comprend une orbitale (3s) sphérique, et 3 orbitales (3p) en larmes d'eau scindées une fois, et 5 orbitales (3d), l'une à symétrie de révolution la 3d(z²-3r²), et 4 en trèfle à 4 lobes : 3d(xy),3d(yz), 3d(zx) et 3d(x²-y²). Voir harmonique sphérique.
- orbitale 3d de révolution :k=0
figure ici
- orbitale 3d(xy):k=0
figure ici
les 3 autres orbitales s'en déduisent par symétrie.
- orbitale 3p :k=1
en larmes d'eau scindées une fois
figure ici
- orbitale 3s, sphérique, scindées deux fois: k=2
figure ici.
Tout ceci est aussi valable pour les espèces iso-électroniques, comme l'ion borique B3+, à condition de changer e2 en Z.e2.
Autres couches
Pour être vraiment encyclopédique, il faudrait aussi évoquer les couches de numéro n supérieur.
État stationnaire d'énergie positive
ébauche
Si l'énergie E est positive, l'état de l'électronde n'est plus lié. On parle d'état de diffusion.La représentation {p} est plus appropriée, mais les calculs utilisent vraiment cette fois la fonction hypergéométrique. Landau fait tous les calculs.
Bibliographie
- E. Hansch, A. Schawlaw & G. Series ; Le spectre de l'hydrogène atomique, Pour La Science 19 (Mai 1979) 46.
- Jean-Louis Basdevant & Jean Dalibard ; Mécanique quantique (avec CD-ROM), Editions de l'école Polytechnique (2002), ISBN 2730208194.
- Claude Cohen-Tannoudji, Bernard Diu & Franck Laloë ; Mécanique quantique, 2 volumes, Hermann (1973), ISBN 2705660747. Grand classique.
- Albert Messiah Mécanique quantique, 2 volumes, Dunod (1959). Réédité en 1995 : ISBN 2100073613. Autre grand classique.
- S.G. Karshenboim et al. (éditeurs) ; The hydrogen atom - Precision physics of simple atomic systems, Lecture Notes in Physics 570, Springer-Verlag (2001). Recueil d'articles de revue sur l' état de l'art en spectroscopie atomique, mesures de fréquences, et mesures de constantes fondamentales. Niveau troisième cycle universitaire.
- Victor Guillemin & Shlomo Sternberg ; Variations on a Theme by Kepler, Providence RI, American Mathematical Society (1990), ASIN 0821810421. Très beau livre.
- Bruno Cordani ; The Kepler Problem - Group Theoretical Aspects, Regularization and Quantization, with Application to the Study of Perturbations, Progress in Mathematical Physics 29, Birkhäuser (2003), ISBN 3-7643-6902-7.
- Stephanie F. Singer, Linear Symmetry and Predictions in Hydrogen Atom, Undergraduate Text in Mathematics, Springer-Verlag (2005), ISBN 3-978-0387-24637-6. De niveau plus simple, mais très moderne et beaucoup de références web.
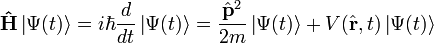
![[\hat p,\hat x] = i\hbar](https://static.techno-science.net/illustration/Definitions/autres/6/680d0305ad707a49bc0017dcc45dc25b_750ff64d3824abe8c12a3e18aa245de9.png)
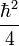
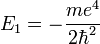
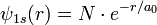
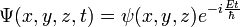
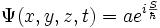
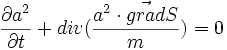
![{\partial S \over \partial t} + {1 \over 2m}(\vec{grad}S)^2 +[V(x,y,z) - {\hbar^2 \over 2m }{\Delta a \over a }] = 0](https://static.techno-science.net/illustration/Definitions/autres/7/73dfbed782e98ecd22908e114a9c7033_cfecd23b0c77eaacccc2934751e5b3be.png)
![\Psi_{n,l,m}(r,\theta,\phi,t) = R_{n,l}(r)\cdot P_{l,m}(\theta)\cdot e^{i[m\phi -{E_n t \over \hbar}]}](https://static.techno-science.net/illustration/Definitions/autres/4/41678cfa5a1b675d7823d6d57d420470_bd7919e90deababdfaf6f946b6526078.png)