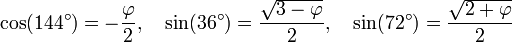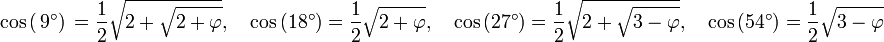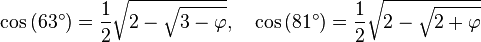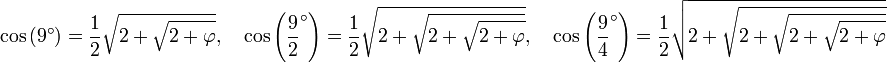Nombre d'or - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
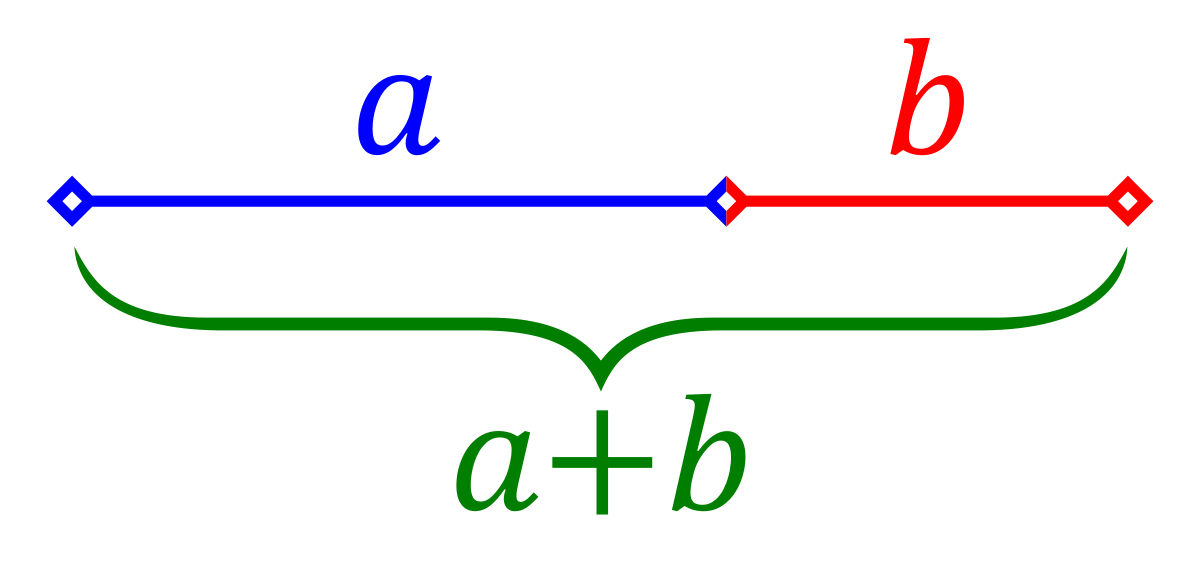
Le nombre d'or est la proportion, définie initialement en géométrie, comme l'unique rapport entre deux longueurs telles que le rapport de la somme des deux longueurs (a+b) sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b) c'est-à-dire lorsque (a+b)/a = a/b. Le découpage d'un segment en deux longueurs vérifiant cette propriété est appelé par Euclide découpage en extrême et moyenne raison. Le nombre d'or est maintenant souvent désigné par la lettre φ (phi) en l'honneur du sculpteur Phidias qui l'aurait utilisé pour concevoir le Parthénon.
Ce nombre irrationnel est l'unique solution positive de l'équation x2 = x + 1. Il vaut exactement :
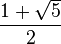
soit approximativement 1,618 033 989. Il intervient dans la construction du pentagone régulier et du rectangle d'or. Ses propriétés algébriques le lient à la suite de Fibonacci et permettent de définir une arithmétique du nombre d'or source de nombreuses démonstrations.
L'histoire de cette proportion commence à une période reculée de l'antiquité grecque. À la Renaissance, Luca Pacioli, un moine franciscain italien, la met à l'honneur dans un manuel de mathématiques et la surnomme divine proportion en l'associant à un idéal envoyé du ciel. Cette vision se développe et s'enrichit d'une dimension esthétique, principalement au cours des XIXe et XXe siècles où naissent les termes de section dorée et de nombre d'or.
Le nombre d'or se trouve parfois dans la nature ou des œuvres humaines, comme dans les étamines du tournesol ou dans certains monuments à l'exemple de ceux conçus par Le Corbusier. Il est aussi étudié comme une clé explicative du monde, particulièrement pour la beauté. Il est érigé en théorie esthétique et justifié par des arguments d'ordre scientifique ou mystique : omniprésence dans les sciences de la nature et de la vie, proportions du corps humain ou dans les arts comme la peinture, l'architecture ou la musique.
Certains artistes, tels le compositeur Xenakis ou le poète Paul Valéry ont adhéré à une partie plus ou moins vaste de cette vision, soutenue par des livres très populaires. À travers la médecine, l'archéologie ou les sciences de la nature et de la vie, la science infirme les théories de cette nature car elles sont fondées sur des généralisations abusives et des hypothèses inexactes.
Géométrie
Proportion
Le nombre d'or possède une première définition d'origine géométrique, fondée sur la notion de proportion :
Définition de la proportion d'or — Deux longueurs strictement positives a et b respectent la proportion d'or si et seulement si, le rapport de a sur b est égal au rapport de a + b sur a :
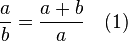
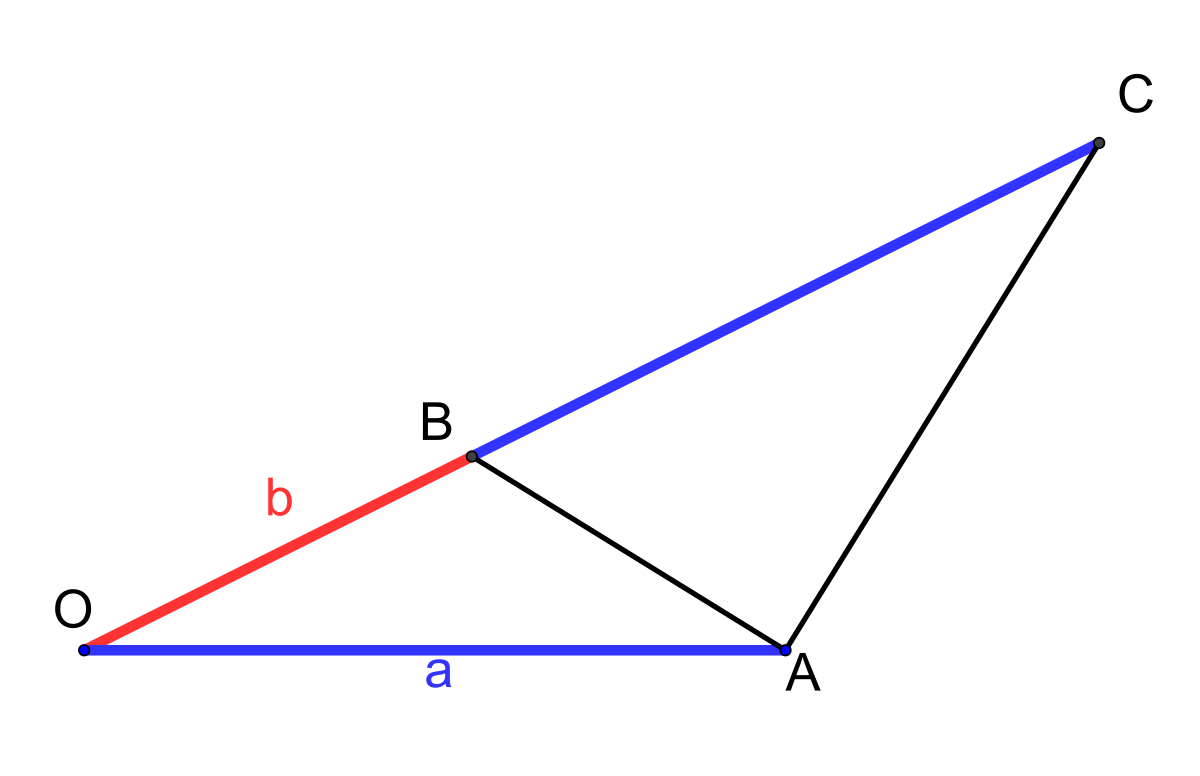
Il existe une interprétation graphique de cette définition, conséquence des propriétés des triangles semblables illustrée par la figure 1. Les segments bleus sont de longueur a et le rouge de longueur b. Dire que la proportion définie par a et b est d'or revient à dire que les triangles OAB et OCA sont semblables. Euclide exprime la proportion d'or, qu'il appelle extrême et moyenne raison, de la manière suivante : Une droite est dite coupée en extrême et moyenne raison lorsque la droite entière est au plus grand segment comme le plus grand segment est au plus petit.
Si a et b sont en proportion d'extrême et de moyenne raison, alors le rapport a / b est constant, ce qui donne une nouvelle définition du nombre d'or :
Définition du nombre d'or — Le nombre d'or est le nombre réel positif, noté φ, égal à la fraction a / b si a et b sont deux nombres en proportion d'extrême et de moyenne raison. Il est donné par la formule :
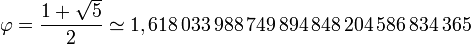
La proportion (1), définissant la proportion d'or, peut être écrite de la manière suivante, obtenue en multipliant l'égalité par a / b :
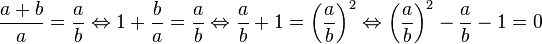
Ce qui revient à dire que φ est solution d'une équation du second degré. Cette propriété donne lieu à une troisième définition :
Définition alternative du nombre d'or — Le nombre d'or est l'unique solution positive de l'équation du second degré suivante :
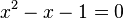
Cette équation est équivalente à celle indiquant que l'inverse de l'inconnue x est égal à x - 1 ou encore que le développement décimal de 1/x est le même que celui de x, auquel on a retranché sa partie entière.
Il existe deux modes de définition du nombre d'or, celle géométrique qui s'exprime en termes de proportion et celle algébrique qui définit le nombre comme l'unique racine positive d'une équation. Cette double approche permet de résoudre un problème d'algèbre, en l'occurrence une équation du second degré, à l'aide de méthode géométrique, on parle d'algèbre géométrique.
-
- Construction de la proportion d'extrême et de moyenne raison :
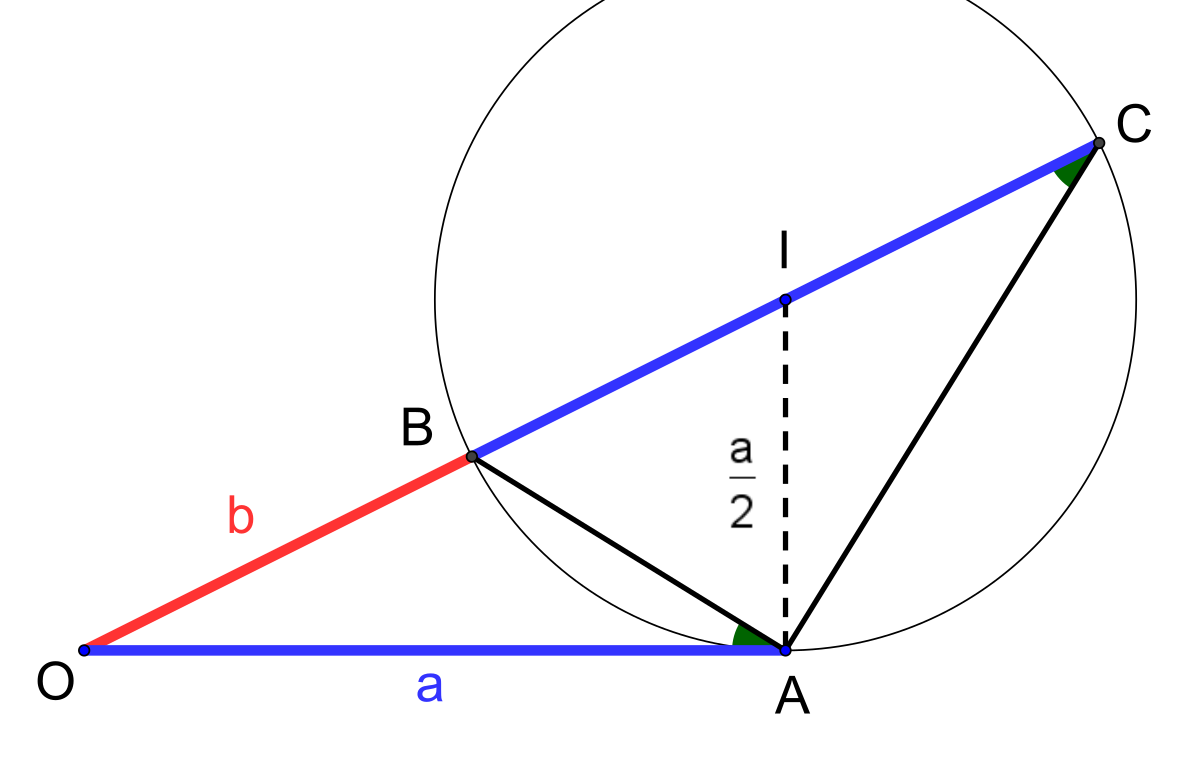
L’objectif est de construire la figure 1. Dans un premier temps, on considère deux points O et A du plan euclidien situés à une distance a l'un de l'autre. Soit I un point tel que les droites AI et OA soient perpendiculaires et tel que la distance AI soit égale à a/2. Soit γ le cercle de centre I et passant par A. Enfin les deux points B et C sont les intersections de la droite OI et du cercle γ dans l'ordre indiqué sur la figure. On définit b comme la distance séparant O de B. Par construction sa distance séparant B de C est égale à a.
Une fois la figure construite, il reste à montrer que les triangles OAB et OCA sont semblables. Pour cela, il suffit de montrer qu'ils possèdent deux angles en commun. L'angle AOB est partagé par les deux triangles, il suffit donc de montrer que l'angle BAO est égal à OCA. Comme la droite OA est tangente au cercle, ce résultat est une conséquence du théorème de l'angle inscrit. Les triangles sont bien semblables.
Deux triangles semblables sont proportionnels, ce qui montre que la base du grand triangle OC est à OA la base du petit triangle, ce que OA un côté du grand triangle est à OB le côté équivalent du petit triangle. On obtient la formule (1).
-
- Unicité de la valeur b :
Soit a une longueur strictement positive, et c un nombre réel plus petit que a tel que la proportion a/c soit d'extrême et de moyenne raison. Soit OBC trois points alignés tel que la distance OB soit égale à c et BC à a. Soit γ le cercle de diamètre BC et A le point de γ tel que la droite OA soit tangente au cercle.
Les arguments de la démonstration précédente montrent que les triangles OAB et OCA sont semblables et que la figure obtenue est celle du paragraphe précédent. En conclusion la valeur c est égale à b, calculé au paragraphe précédent. Ceci montre l'unicité de b.
-
- Détermination géométrique de φ :
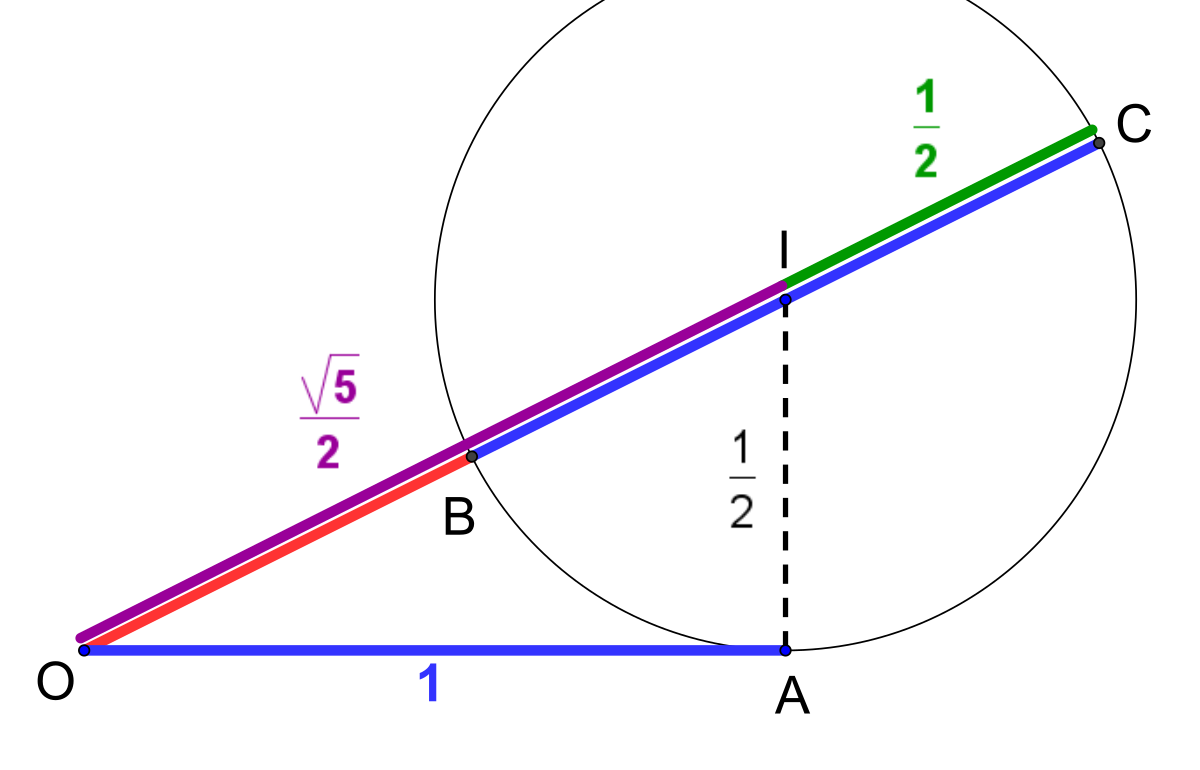
Pour calculer la valeur de φ, on peut utiliser le fait que si a et b sont en extrême et moyenne proportion, alors (a + b) / a est égal à φ. La longueur a peut être choisie quelconque, une méthode simple consiste à la choisir égale à 1. La valeur φ est alors égale à a + b ou encore à 1 + b. La longueur de OC est égale à la somme de la longueur de OB et de celle de EB, et donc à b + 1, le nombre d'or. Ici le nombre 1 représente le diamètre du cercle C de rayon 1/2, par construction.
La longueur de OC est égale à φ et aussi à la somme de la longueur de OI et de IC. Le théorème de Pythagore montre que la distance entre O et I est égale à √5/2, la longueur de la diagonale d'un rectangle de côté de longueurs 1 et 1/2. Celle de I à C est égale au rayon du cercle 1/2. La longueur OC est à la fois égale au nombre d'or φ et à 1/2.(1+√5), ce qui montre le résultat recherchée.
-
- Détermination algébrique de φ :
Une autre solution pour le calcul de φ consiste à faire usage de la troisième définition. La valeur φ est donnée par la solution positive de l'équation du second degré :
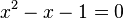
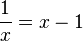
Le discriminant de l'équation du second degré est égal à 1 + 4 = 5, il existe deux solutions, une seule est positive, on en déduit :
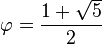
Un calcul ne faisant pas appel au discriminant est proposé en introduction dans l'article équation du second degré.
Rectangle et spirale d'or
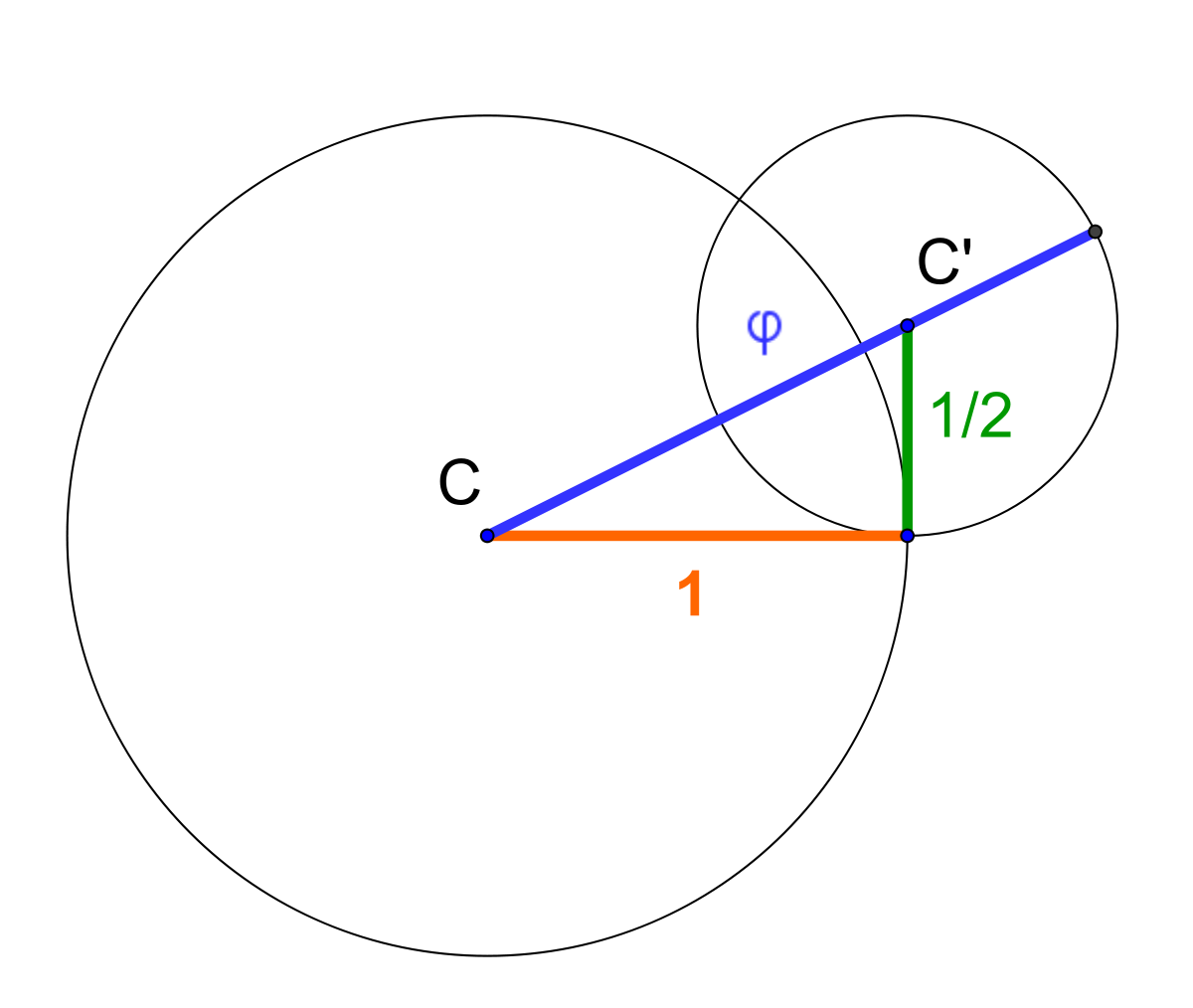
Les calculs précédents permettent, à l'aide d'une règle et d'un compas de dessiner une proportion d'extrême et de moyenne raison. La méthode est illustrée sur la figure de gauche. On dessine un cercle de centre C et de rayon 1 (en orange). Puis, de l'extrémité du rayon, on élève un segment (en vert) perpendiculaire au rayon, de longueur 1/2, et on trace le cercle de centre C' et de rayon 1/2. Le segment bleu qui a pour extrémités C et le point du cercle C' dans le prolongement de C C' est de longueur φ.
Cette méthode permet aussi de construire un rectangle d'or, c'est-à-dire un rectangle de longueur a et de largeur b tel que a et b soient en proportion d'extrême et de moyenne raison. En d'autres termes, un rectangle est dit d'or si le rapport entre la longueur et la largeur est égal au nombre d'or.
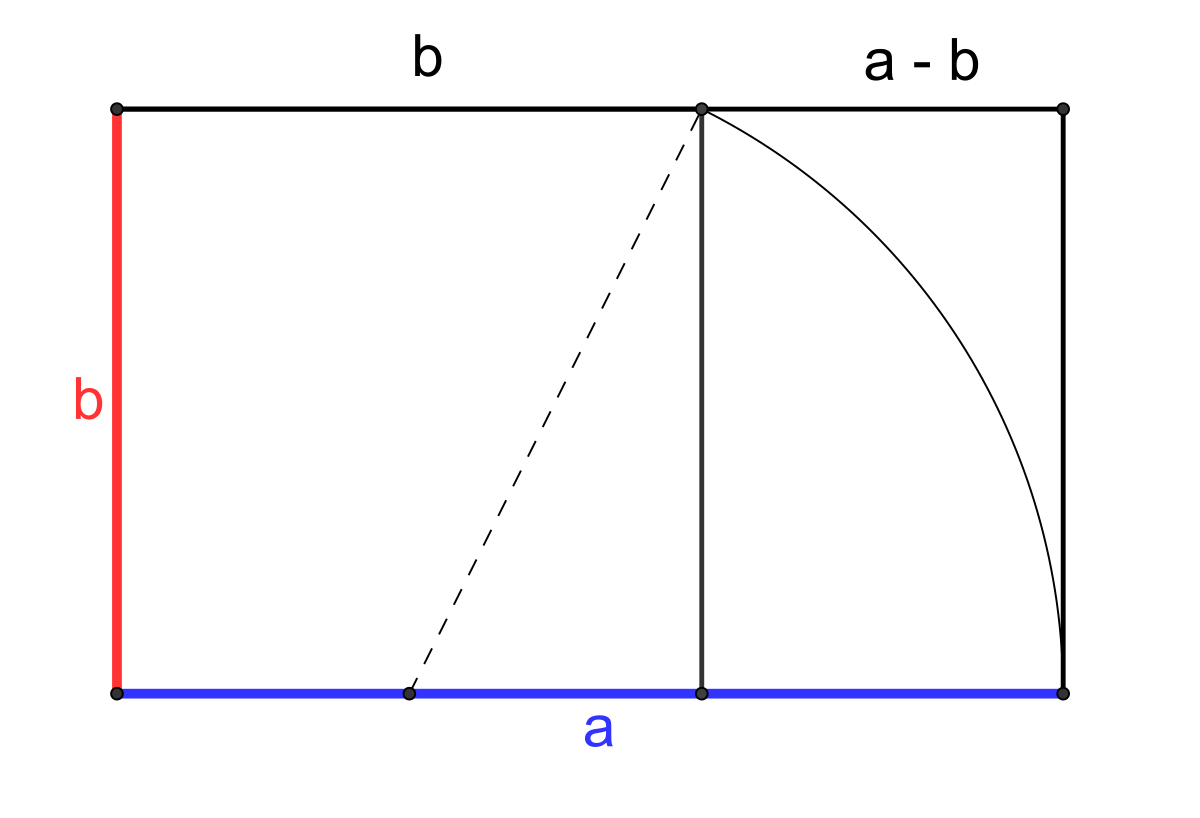
Pour tracer un rectangle d'or de longueur a et de largeur b, le plus simple est de dessiner un carré de côté b. En prenant le milieu de la base comme centre, on trace un cercle passant par les deux sommets opposés. L'intersection de la droite prolongeant la base du carré et du cercle détermine l'extrémité de la base du rectangle d'or. Il apparait comme construit par l'adjonction à un carré de côté de longueur b, d'un rectangle de côtés de longueur b et a - b, comme le montre la figure de droite. Un rapide calcul montre que ce rectangle est encore d'or :
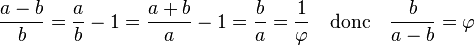
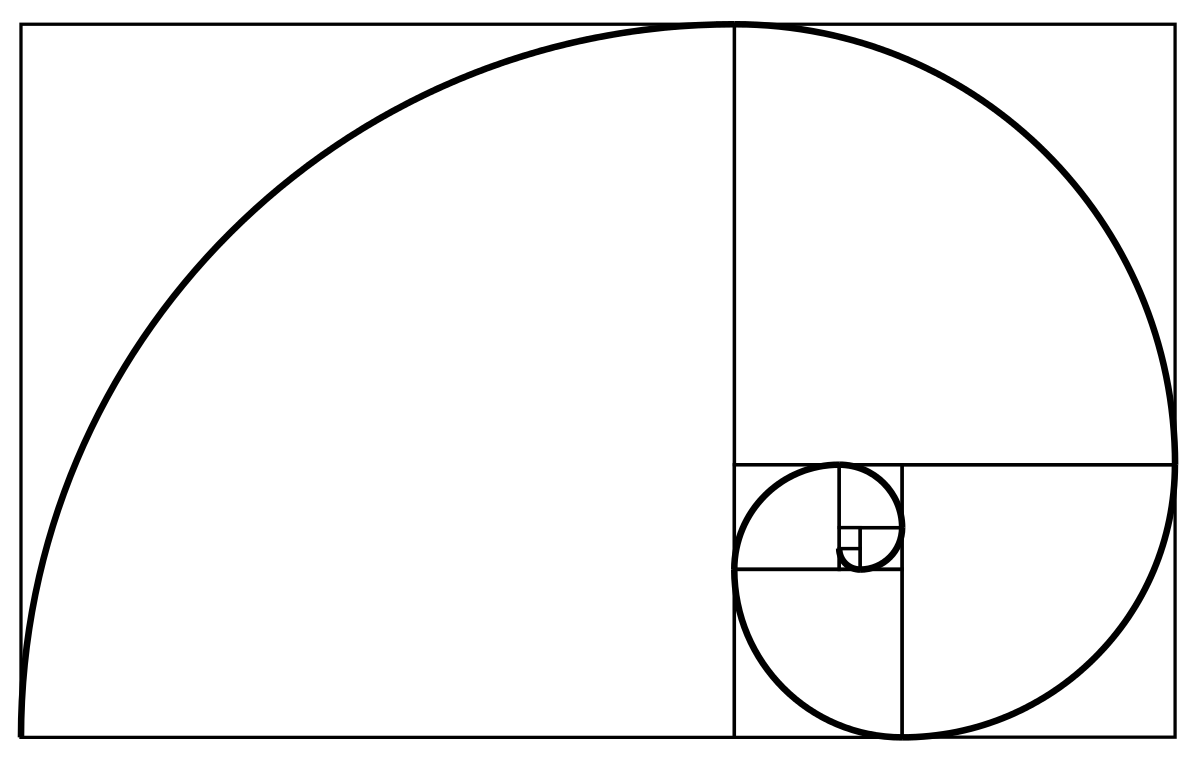
Il est possible de réitérer le processus précédent et d'intégrer un carré de côté a - b dans le rectangle d'or de côté b, a - b, comme indiqué sur la figure de gauche. Cette méthode peut être prolongée indéfiniment. Si, dans chaque carré est dessiné un quart de cercle d'extrémités deux côtés du carré, comme sur la figure, on obtient une spirale. Ce graphique est une bonne approximation d'une spirale d'or, d'équation polaire :
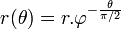
Cette spirale est un cas particulier de spirale logarithmique. Comme toute spirale de cette famille, elle possède une propriété caractéristique, si A est un point de la spirale, l'angle entre la droite passant par le centre de la spirale et A fait un angle constant avec la tangente à la spirale en A. Une telle spirale est dite équiangle.
D'autres figures se dessinent à l'aide du nombre d'or à l'instar de l'oeuf d'or.
Pentagone et pentagramme
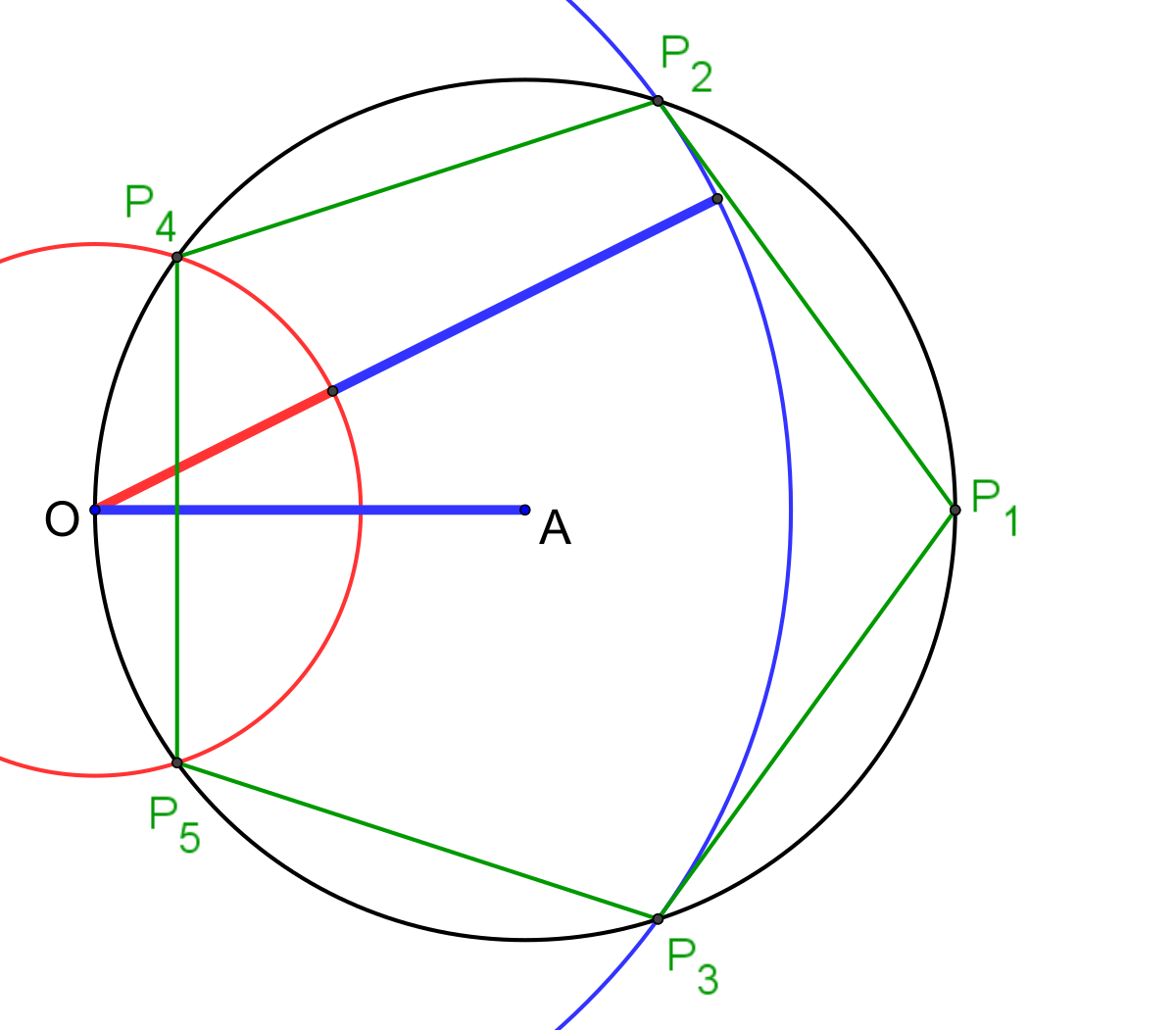
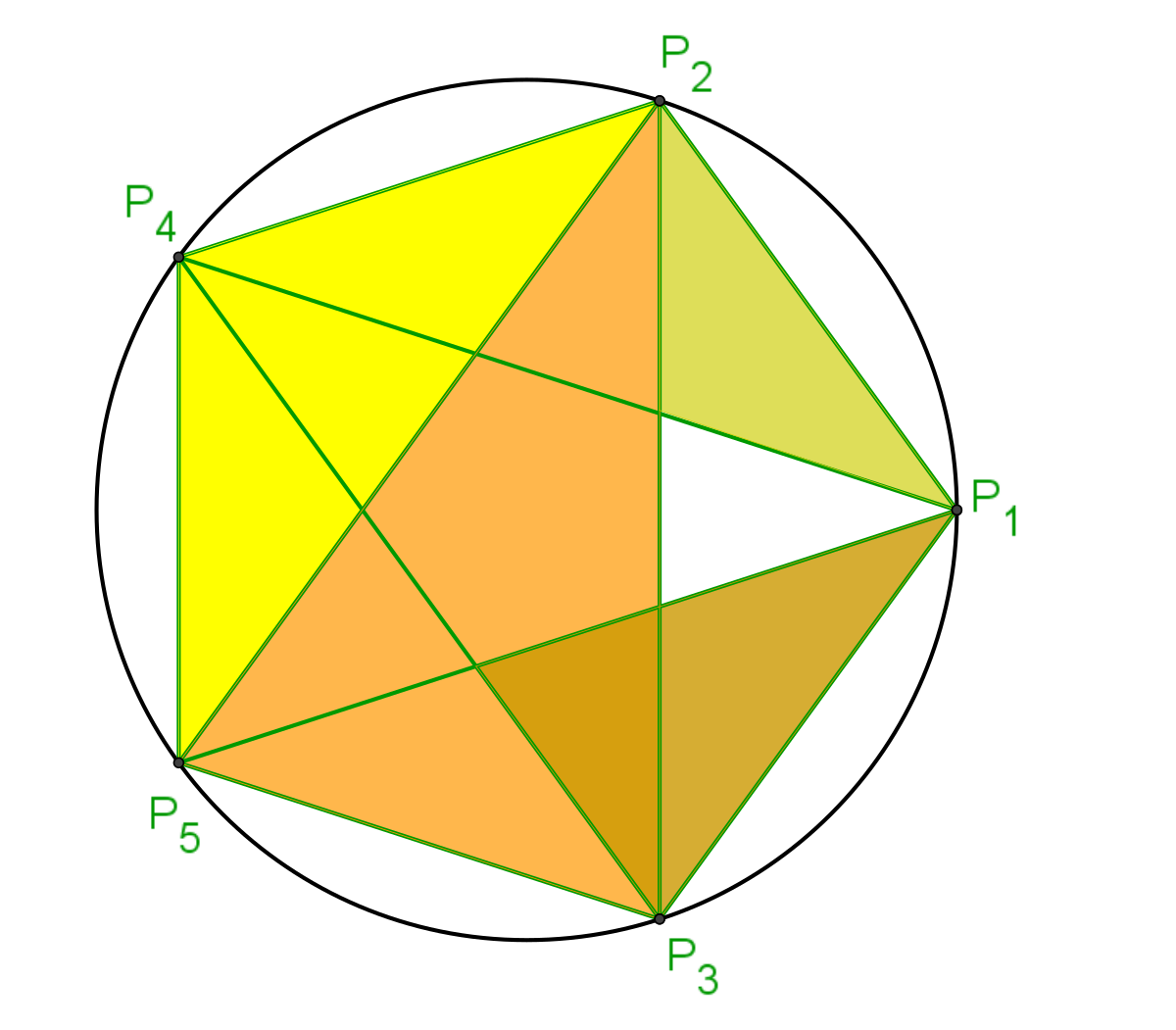
Un pentagone se construit à l'aide de la proportion d'extrême et moyenne raison. Soit un cercle de diamètre OP1 et de rayon a, illustré sur la figure de gauche. Si b est le nombre réel plus petit que a tel que a et b soit en proportion d'or, et P2, P3, P4 et P5 les intersections du cercle de diamètre OP1 avec les deux cercles de centre O et de rayon a + b et b, alors les cinq points Pi définissent un pentagone.
Le pentagramme associé, c'est-à-dire la figure composée des cinq diagonales du pentagone (cf figure de droite), contient aussi de multiples proportions d'extrêmes et moyennes raisons. Elles s'expriment simplement à l'aide de triangles isocèles dont les longueurs des côtés sont en proportion d'or. De tels triangles sont appelés triangles d'or. Il en existe de deux types différents, les jaunes ayant une base proportionnelle à a et deux côtés à b et les orange ayant une base proportionnelle à b et deux côtés à a. Les triangles foncés sont semblables aux plus clairs de même couleur, la proportion entre clair et foncé est encore d'or.
Les triangles jaunes possèdent deux angles de 36°, soit le cinquième d'un angle plat et un de 108°, soit les trois cinquièmes d'un angle plat. Un tel triangle est parfois appelé triangle d'argent. Les triangles orange possèdent deux angles de 72°, soit les deux cinquièmes d'un angle plat et un angle de 36°. Avec des triangles d'or et d'argent dont les côtés sont toujours a et b, il est possible de paver intégralement un plan euclidien de manière non périodique. Un tel pavage est dit de Penrose.
La trigonométrie permet de montrer les différentes propriétés du paragraphe, il est aussi possible d'établir ces résultats à l'aide de la géométrie.
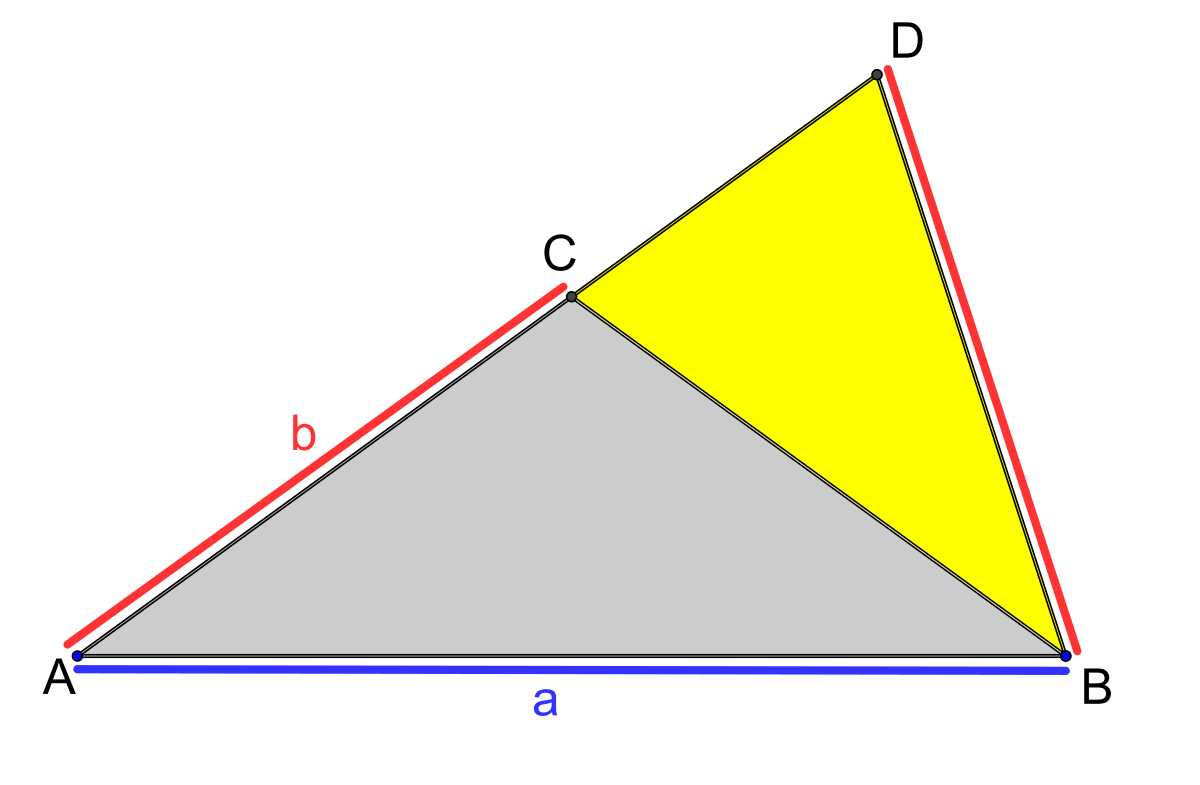
Le premier lemme est la clé des différentes preuves. Soient a et b avec a > b, deux longueurs en proportion d’extrême et de moyenne raison. Soit ABD un triangle d'or tels que A et B soient situés à une distance a l’un de l’autre et B et D à une distance b.
-
- Soit C le point du segment AD tel que la distance AC soit égale à b alors le triangle BCD est un triangle d'or et le triangle ABC est un triangle d’argent
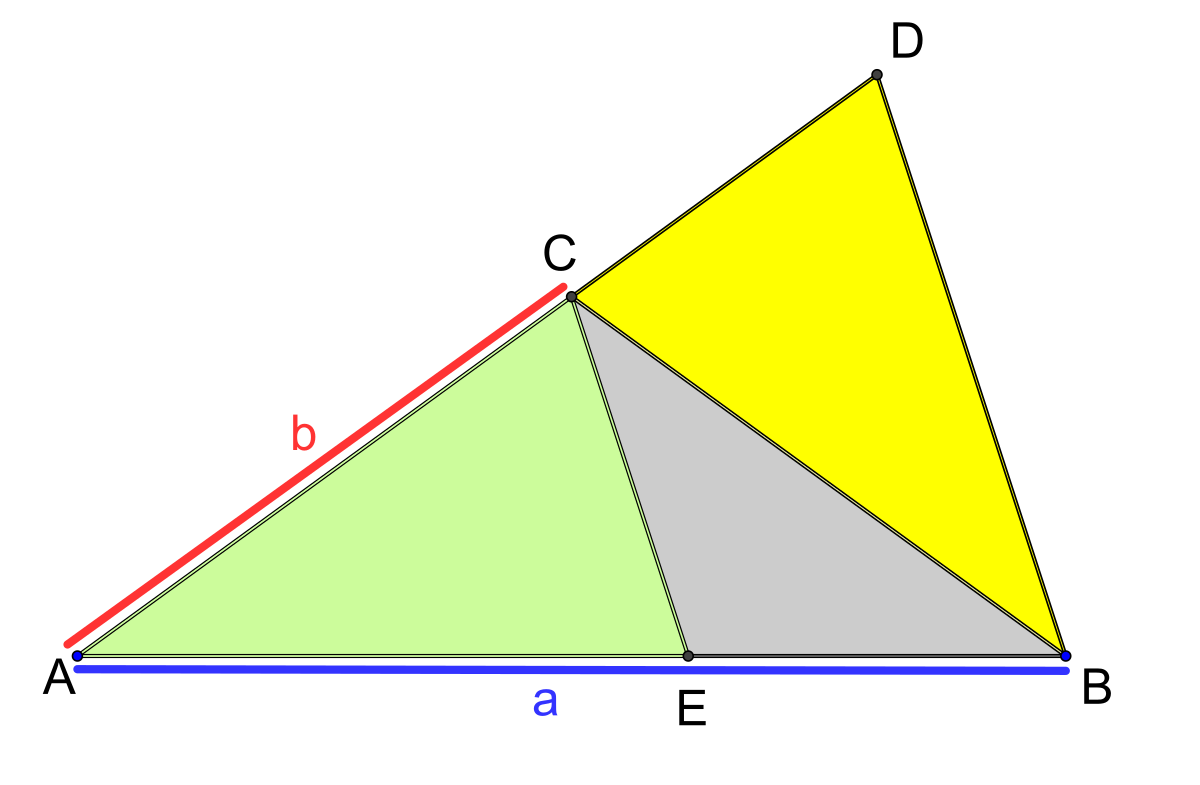
Cette proposition correspond à la figure de droite. Par construction, les distances AB et AD sont égales à a. Considérons le point E du segment AB situé à b de A et montrons que le triangle AEC (en vert) est égal à BCD (en jaune). Il suffit de montrer qu’ils disposent d’un angle et de deux côtés égaux. Les deux triangles AEC et ABD sont semblables (car tous deux isocèles de même sommet) et dans un rapport de a/b. Comme la distance entre B et D est égale à b, celle entre C et E est égale à a - b (car b/(a - b) = a/b). Or cette distance est la même que celle qui sépare C et D. Le caractère semblable des triangles ACE et ADB montre que l’angle ACE est égal à ADB. Enfin, la distance DB est égale à celle de AC. Les deux triangles disposent bien de deux côtés et d’un angle égaux, ils sont identiques. Le triangle ACE étant semblable au triangle d'or ADB, c'est un triangle d'or ainsi que le triangle BDC. Il est en proportion a/b avec le triangle initial.
Il reste à prouver que le triangle ACB est bien d'argent. Il suffit de prouver que la distance de B à C est égale à b. Or le triangle BDC étant un triangle d'or, on sait que la distance BC est égale à celle de BD et donc à b, ce qui termine la démonstration.
-
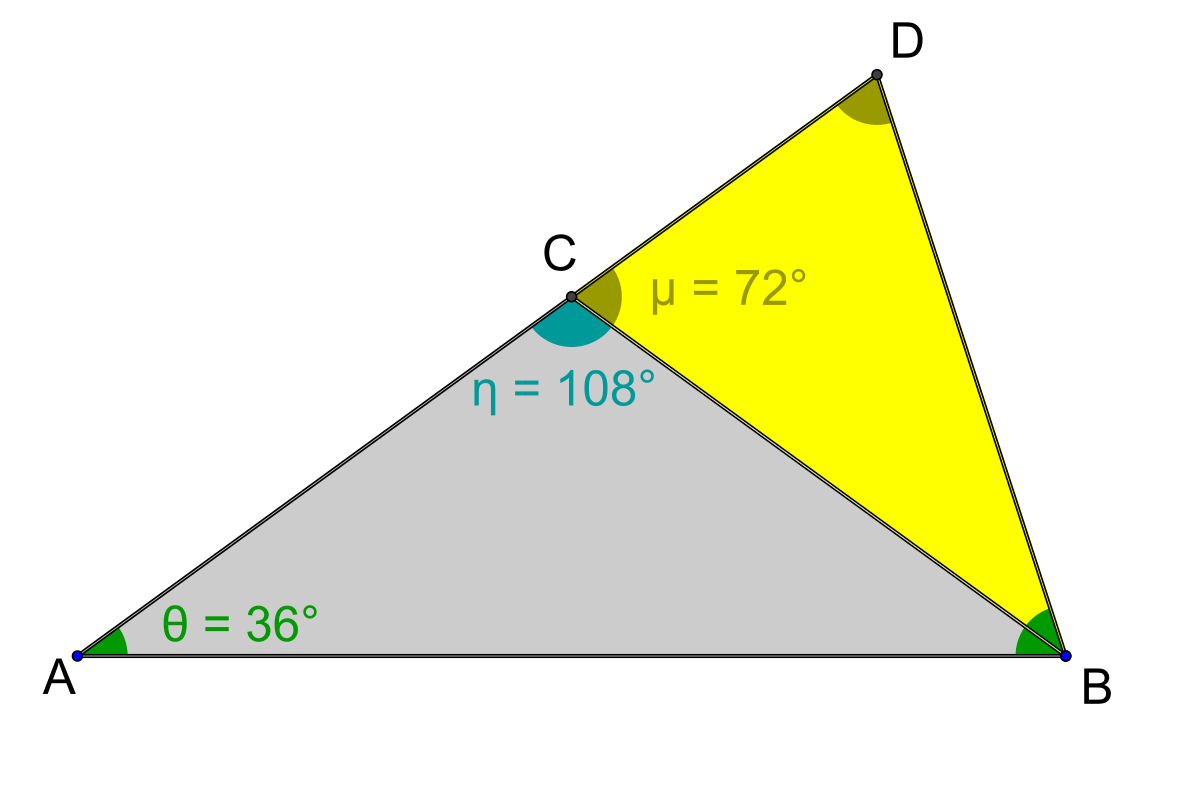
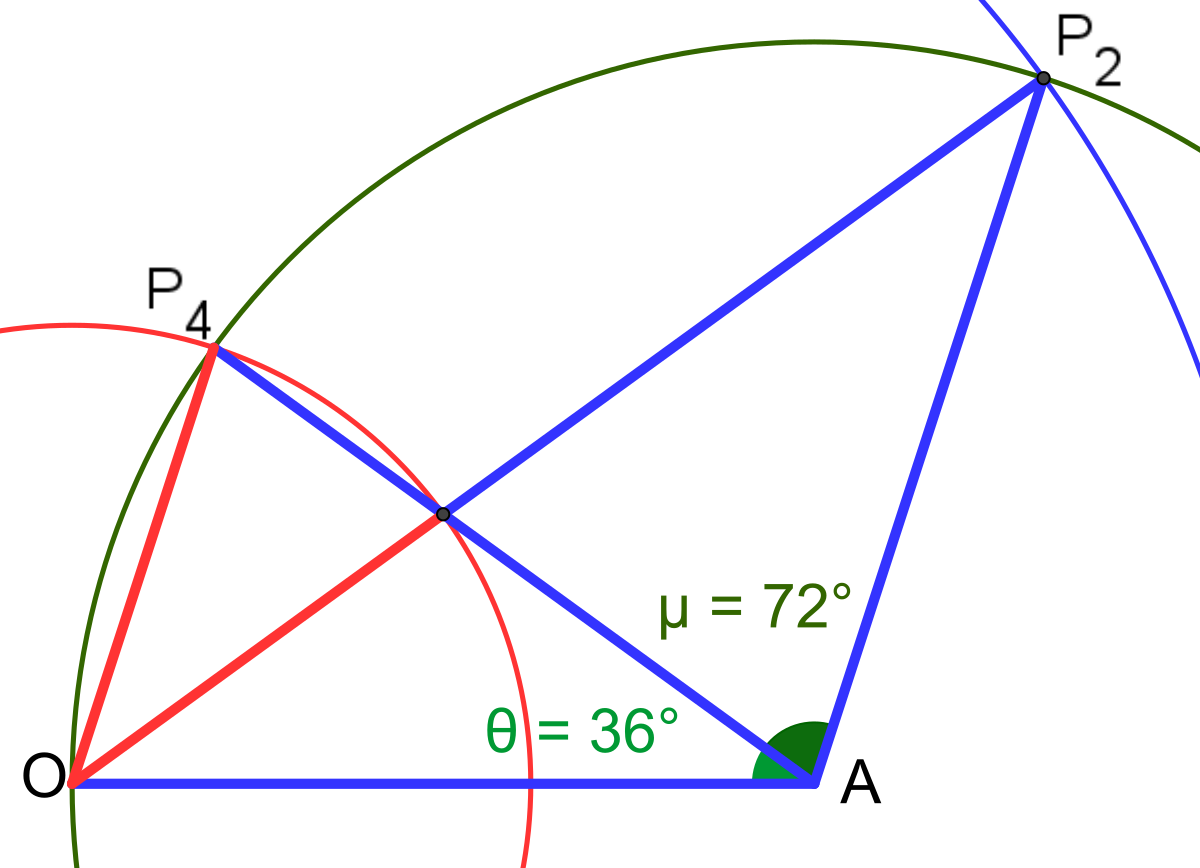
- Un triangle d'or est composé de deux angles de 72° et un de 36°, un triangle d'argent contient deux angles de 36° et un de 108° :
Le lemme précédent nous affirme que le triangle ABC est isocèle de sommet C. Donc l'angle DCB est égal au double de l'angle CAB soit avec les notations de droite : μ = 2θ. D'autre part, le triangle BCD étant aussi un triangle d'or, il est isocèle de sommet B. Ses angles sont θ, 2θ, 2θ. La somme des angles valant 180°, on a 5θ=180°, soit θ=36° Il vient alors immédiatement que μ = 2θ = 72° puis que η = 180 - μ = 108°
On remarque que θ est égal à un cinquième de demi-tour, μ à deux cinquièmes et η à trois cinquièmes.
-
- Les points P1, P2, P3, P4 et P5 de la figure 3, forment un pentagone :
La méthode utilisée ici consiste à montrer que si deux sommets sont consécutifs, alors leur angle avec le centre du cercle est de 72°.
-
- L'angle P4AP5 est de 72°:
Cette première étape est la conséquence du fait que les points P4 et P5 sont définis comme l'intersection du cercle de centre O et de rayon b avec le cercle de centre A et de rayon a. les triangles P4AO et OAP5 sont d'or, les angles P4AO et OAP5 font chacun 36°, ce qui permet de conclure.
-
- L'angle P4AP2 est de 72° :
La distance entre O et P2 est égale à a + b, celle entre O et A ainsi que celle entre A et P2 est égal à a. On en déduit que le triangle OAP2 est un triangle d'argent. L'angle OAP2 fait donc 108°. Comme l'angle P4AO fait 36°, par différence, on obtient que l'angle P4AP2 est de 108° - 36° soit 72°
-
- L'angle P2AP0 est de 72° :
L'angle OAP2 fait 108° et l'angle OAP0 est plat donc l'angle P2AP0 est égal à 180° - 108°, soit 72°.
-
- Conclusion :
Il reste encore à mesurer les angles P5AP3 et P3AP0. Pour cela, il suffit de remarquer que la droite OA est un axe de symétrie du pentagone, en conséquence l'angle P5AP3 est égal P4AP2 et P3AP0 est égal à P1AP0, ce qui termine la démonstration.
Trigonométrie
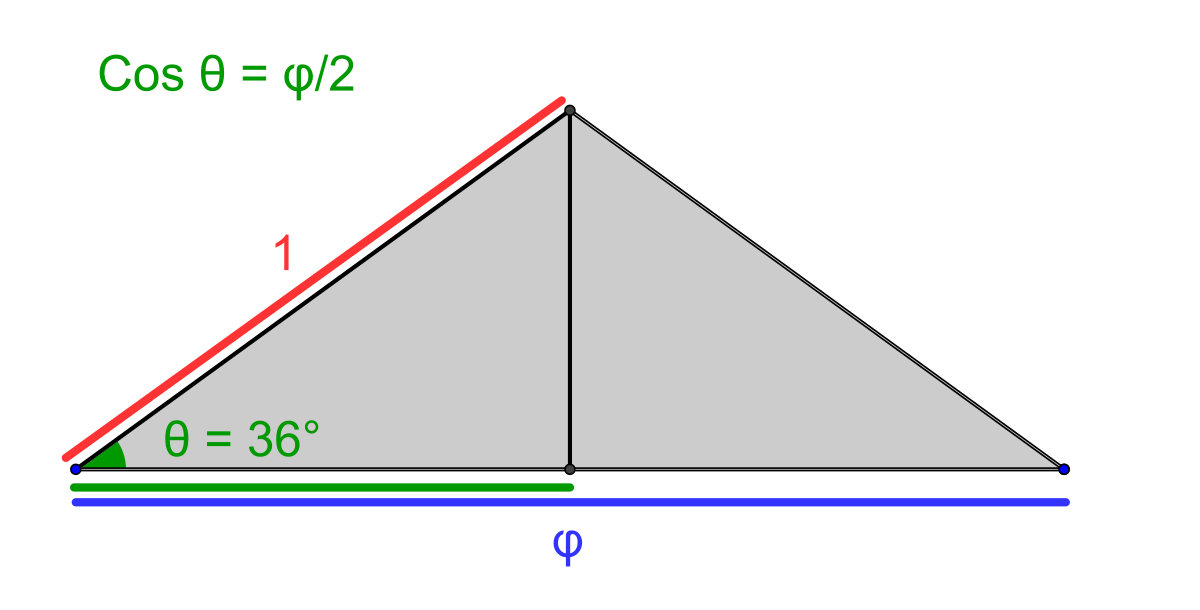
L'analyse des mesures des triangles d'argent et d'or permettent de déterminer les valeurs trigonométriques associées au pentagone. Considérons un triangle d'argent de base φ et donc de côtés adjacents de longueur 1. Ce triangle, coupé en son milieu, comme sur la figure de droite, est un triangle rectangle d'hypoténuse de longueur 1. Sa base est de longueur φ/2 car elle correspond à la demi-base du rectangle d'argent. On en déduit que le cosinus de 36° est égal à φ/2. Un raisonnement analogue s'applique au triangle d'or. Les côtés ont toujours une longueur 1, la base est en proportion d'or donc de longueur φ - 1. On en déduit que le cosinus de 72° est égal à (φ - 1)/2. À partir de ces valeurs et de différentes formules, il est possible de calculer les images par les fonctions trigonométriques des multiples ainsi que les moitiés de l'angle 36°.
Une autre manière de déterminer les différentes valeurs caractéristiques d'un pentagone consiste à utiliser le plan complexe. Les sommets sont les racines du polynôme cyclotomique X5 - 1. Sa résolution est particulièrement aisée car 5 est un nombre premier de Fermat, c'est-à-dire qu'il existe un entier n tel que 5 est égal à 2n + 1. Si p est un nombre premier, le polynôme régulier à p côtés est constructible à la règle et au compas si et seulement si, p est un nombre de Fermat. Dans ce cas, l'extraction des racines du polynôme cyclotomique s'obtient à l'aide de résolution d'équations du second degré. Ce cas est traité dans l'article Polynôme cyclotomique.
En appliquant la formule de l'angle moitié :
-
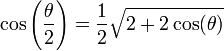
ainsi que les formules d'angle double et d'angle complémentaire, on peut déterminer le cosinus de tous les angles multiples de 9°. Certaines s'expriment à l'aide du nombre d'or :
On peut aussi déterminer le cosinus des angles de la forme
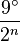
De manière générale :