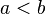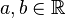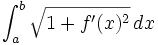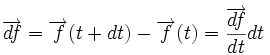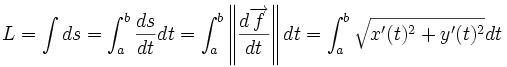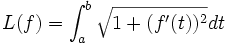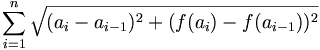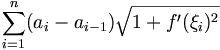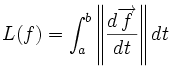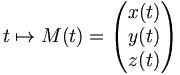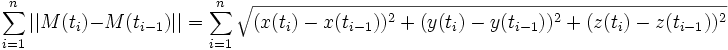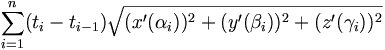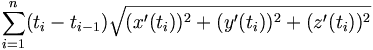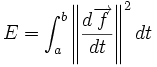Longueur d'un arc - Définition
Intuitivement, la longueur d’une courbe ou d'un arc (portion) de courbe est la longueur de ficelle qu'il faudrait dérouler pour la parcourir complètement. Cette longueur peut être obtenue si on connaît le temps de parcours et la vitesse.
Pour donner une définition générale de la longueur d'un arc, il faut commencer par formaliser la notion de distance, en général dans le cadre d'un espace euclidien. On sait alors mesurer la longueur de courbes simples : les lignes polygonales.
Les Anciens sans disposer d'un procédé de calcul explicite, se contentaient d'approcher les longueurs de courbe, en considérant des lignes polygonales joignant des points de la courbe. C'est la méthode d'exhaustion, qui avait été initiée par Eudoxe de Cnide et Archimède pour les calculs d'aires.
Ces calculs approchés de longueur peuvent servir de fondement à une définition générale permettant de dépasser la vision intuitive de la longueur. La longueur de l'arc sera la borne supérieure, si elle existe, des longueurs de telles lignes polygonales.
Lorsque la courbe est paramétrée de façon suffisamment régulière, on obtient une formule explicite pour la longueur, issue du calcul différentiel. On peut alors utiliser la notion d'abscisse curviligne qui est une sorte de longueur algébrique, tenant compte de l'orientation, et qui permet de reparamétrer la courbe de façon à s'affranchir des considérations sur la vitesse de parcours.
Présentation moderne : courbe rectifiable et longueur
Approche par la notion de vitesse
Voici une première façon d'introduire la longueur, à partir de la notion un peu floue de "longueur d'un vecteur déplacement infinitésimal". Comme historiquement le calcul infinitésimal a précédé la définition précise des notions de limite et de borne supérieure, cette première définition de la longueur relève d'une tradition différente de la suivante et peut sembler plus parlante.
On se place pour ce calcul dans le plan euclidien, rapporté à un repère orthonormal. On envisage un arc paramétré de classe
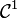
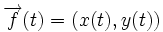
On peut parler du vecteur déplacement infinitésimal
Notons sa norme ds : c'est la longueur infinitésimale parcourue pendant l'intervalle de temps dt. Alors la longueur de l'arc est obtenue en sommant ces longueurs élémentaires
On pourra résumer cette formule en exprimant la valeur de la longueur infinitésimale sous la forme
- ds2 = dx2 + dy2
D'autres formules peuvent s'établir de la même façon (pour des courbes de l'espace euclidien à 2, 3 dimensions), avec, suivant le système de coordonnées choisi
- ds2 = dx2 + dy2 + dz2 coordonnées cartésiennes dans l'espace
- ds2 = dr2 + r2dθ2 coordonnées polaires dans le plan
- ds2 = dr2 + r2dθ2 + dz2 coordonnées cylindriques dans l'espace
- ds2 = dr2 + r2dθ2 + r2sin2θdφ coordonnées sphériques dans l'espace
-
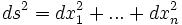
Pour donner à ces formules un sens rigoureux, il faudrait introduire les notions générales de forme quadratique et de tenseur métrique. Pour obtenir les formules usuelles, il suffit cependant de manipuler l'interprétation en termes d'éléments de longueur infinitésimaux.
Le s qui pointe son nez dans ces formules est cependant une quantité intéressante pour elle-même : l'abscisse curviligne, version algébrisée de la longueur.
Notions générales de courbe rectifiable et de longueur d'arc
Le paragraphe précédent masquant un certain nombre de difficultés et n'étant valable que pour des arcs dérivables (pour lesquels on peut parler de vecteur vitesse), on procède à une définition plus générale et plus géométrique.
Définitions
Une courbe est rectifiable si les lignes polygonales inscrites sur celle-ci sont de longueur uniformément bornée.
Si
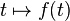
| L(P) = | ∑ | MiMi + 1 |
| i |
La courbe est dite rectifiable si la longueur L(P) est majorée par une constante C indépendante du choix des ti.
La longueur de la courbe est alors par définition le supL(P) pris sur toutes les lignes polygonales possibles.
Remarques :
- cette définition a un sens dès lors que l'espace est muni d'une norme
- la notion de courbe rectifiable, de longueur sont indépendantes du choix de paramètre ;
- la courbe donnée par la graphe de
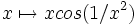
- le graphe d'une fonction numérique (y=f(x)) continûment dérivable définie sur un segment [a,b] est rectifiable avec la formule
Considérons une courbe du plan ?2, et supposons que la courbe soit le graphe d'une fonction continûment dérivable du segment [a, b] dans ?.
Soit σ=(a0, …, an) une subdivision de [a, b]. Nous pouvons lui associer la ligne polygonale de sommets : (ak, f(ak)) (k = 0,…,n). Sa longueur est la somme :
D’après le théorème des accroissements finis, pour tout i de {1, 2, ..., n}, il existe ξi dans l’intervalle ai-1, ai[ tel que
- f(ai)-f(ai-1)=f'(ξi )(ai-ai-1)
La longueur de la ligne polygonale s’écrit :
Nous reconnaissons une somme de Riemann de la fonction
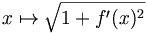
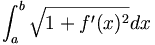
- un arc paramétré par t dans [a,b] et continûment dérivable est rectifiable avec la formule
Considérons une courbe paramétrée de ?3 définie par :
où x, y, z sont des fonctions continûment différentiables sur un segment [a, b]. Notons | | . | | la norme euclidienne de ?3. Considérons σ=(t0, …, tn) une subdivision de [a, b]. La somme
représente la longueur de la ligne polygonale dont les sommets sont les points M(ti).
D’après le théorème des accroissements finis, pour tout i dans {1, …, n}, il existe αi, βi et γi dans ]ti-1, ti[ tels que :
- x(ti)- x(ti-1)= (ti-ti-1) x’(αi)
- y(ti)- y(ti-1)= (ti-ti-1) y’(β i)
- z(ti)- z(ti-1)= (ti-ti-1) z’(γ i)
La somme est égale à :
En utilisant l’uniforme continuité sur [a, b]3, de l’application
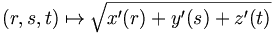
tend vers 0 lorsque le pas des subdivisions tend vers 0. Cette dernière somme est une somme de Riemann de la fonction:
-
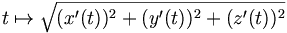
L’intégrale
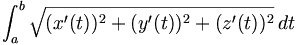
Si l'arc était lipschitzien, il serait encore rectifiable.
Calculs de longueurs classiques
La formule de calcul de la longueur faisant intervenir une intégrale de racine carrée, il est fréquent que la longueur ne puisse se calculer à l'aide de fonctions usuelles.
Ainsi un problème en apparence aussi simple que de calculer la circonférence de l'ellipse en fonction des demi-axes conduit à des intégrales qu'on ne peut pas expliciter plus avant : on parle d'ailleurs d'intégrales elliptiques (de seconde espèce en l'occurrence).
Courbes pour lesquelles le calcul est possible à l'aide des fonctions usuelles
- le segment de droite
- l'arc de cercle
- l'arc de parabole
- l'arc de chaînette
- l'arc de cycloïde, d'hypocycloïde, d'épicycloïde
- l'arc de spirale logarithmique
- ...
Continuité de la fonction longueur
Posons la question en termes flous : deux courbes " proches " ont-elles des longueurs voisines ?
Voici un exemple négatif. On prend le graphe de la fonction constante égale à 0 sur [0,1]. Celui-ci est de longueur 1. On fabrique facilement une suite de fonctions continues sur [0,1], rectifiables, qui converge uniformément vers f et dont la longueur ne converge pas vers 1.
Par exemple : f1 est une fonction triangle avec des pentes 1 sur [0,1/2] et -1 sur [1/2,1]. Puis f2 est une fonction formée de deux triangles, avec des pentes 1 sur [0,1/4], -1 sur [1/4,1/2], 1 sur [1/2,3/4], -1 sur [3/4,1], et ainsi de suite (4,8,16 triangles, ...). Chacune des fonctions fn a un graphe de longueur

Pour obtenir des résultats de continuité pour l'application " longueur ", il ne faut donc pas travailler avec la norme de la convergence uniforme. Il faudrait plutôt une norme du type de celles des espaces de Sobolev.
L'histoire du calcul des longueurs d'arc
Pendant une très longue période de l'histoire des mathématiques, la notion de longueur d'arc a paru parfaitement inaccessible au calcul. La possibilité de définir une telle longueur a même souvent été mise en doute, comme ce fut le cas pour les limites.
Méthode d'exhaustion
Les premiers calculs concernant les longueurs d'arc furent donc des calculs approchés, suivant la méthode d'exhaustion. Divers géomètres, avec une virtuosité de plus en plus grande, s'ingénièrent à inscrire sur les courbes remarquables des lignes polygonales, avec un découpage de plus en plus fin. Ils obtenaient ainsi une valeur approchée de plus en plus précise pour la longueur. La même méthode servait à effectuer des calculs approchés pour les aires.
Au XVIIe siècle, la méthode d'exhaustion permit la rectification, par des procédés géométriques, de plusieurs courbes transcendantes : la spirale logarithmique par Torricelli en 1645 (attribué par certains à John Wallis dans les années 1650), la cycloïde par Christopher Wren en 1658, et la caténoïde par Gottfried Leibniz en 1691.
En 1659 eut lieu la rectification de la première courbe algébrique non triviale, la parabole semi-cubique (ou parabole de Neile, du nom de son découvreur).
Premiers pas en calcul infinitésimal
Avant même le plein avènement du calcul infinitésimal, les premières fondations pour obtenir la formule intégrale donnant la longueur d'arc furent jetées indépendamment par Hendrik van Heuraet et Pierre de Fermat.
En 1659 van Heuraet publia une construction par laquelle la longueur d'arc pouvait s'interpréter comme l'aire sous une courbe - donc effectivement une intégrale - et appliqua cela au cas de la parabole. En 1660, Fermat publia une théorie plus générale, englobant ce résultat, dans De linearum curvarum cum lineis rectis comparatione dissertatio geometrica.
Problèmes de minimum
Plus court chemin entre deux points
Il est bien connu qu'en géométrie euclidienne, la ligne droite est le plus court chemin entre deux points.
- si on prend la définition générale d'arc rectifiable, la propriété est immédiate
En effet la longueur de l'arc est supérieure à celle de la ligne droite joignant origine et extrémité de l'arc (qui est une ligne polygonale particulière). Toutes les autres lignes polygonales sont d'ailleurs de plus grande longueur par l'inégalité triangulaire.
- si on utilise comme expression de la longueur l'intégrale de la norme du vecteur dérivé :
On appelle A et B les extrémités de l'arc et on compare la longueur de l'arc avec celle de l'arc obtenu par projection orthogonale sur (A,B). Comme la projection orthogonale diminue les normes, notre arc est plus long qu'un arc tracé sur une droite et reliant A à B, lui même plus long que l'arc [A,B].
Longueur et énergie
Dans de nombreux problèmes de minimisation, on peut essayer d'utiliser l'énergie de l'arc
qui a l'avantage de ne pas faire intervenir de racine carrée.
En outre énergie et longueur ne sont pas sans lien : lorsque l'arc admet une paramétrage normal (à vitesse uniforme 1), longueur et énergie sont égales. La courbe d'énergie minimale entre deux points est encore la droite, parcourue à vitesse uniforme.
Cette énergie représente une "énergie élastique de déformation". On la fait intervenir par exemple dans l'inégalité isopérimétrique ou la recherche de géodésiques.
Autres problèmes de minimisation
- Inégalité isopérimétrique : le cercle est la courbe fermée de plus petite longueur enserrant un domaine d'aire donnée.
- les splines minimisent l'énergie entre deux points avec vecteurs vitesses initiales donnés.
- la recherche de plus courts chemins dans un espace courbe, ou géodésiques, fait intervenir un cadre beaucoup plus général : la géométrie riemannienne. On donne ci-dessous l'expression de la longueur dans ce cadre.
- la brachistochrone minimise le temps de parcours entre deux points, pour des particules soumises à une accélération constante (pesanteur). Ceci permet de faire un parallèle entre présence de ce champ d'accélération et recherche de plus court chemin dansun espace courbe (cf relativité générale).
Les deux derniers problèmes demandent de faire appel aux techniques du calcul des variations.
Généralisation : longueur d'un arc dans une variété riemannienne
Supposons que M est une variété riemannienne et que γ: [a, b] → M est une courbe continuement dérivable sur M, alors on peut définir la longueur et l'énergie de cette courbe par :
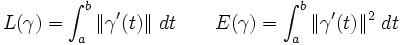
où
La recherche de plus courts chemins, qu'il faut envisager sous deux aspects : local et global, relève alors du calcul de géodésiques.
Définition
La longueur de la représentation graphique d'une fonction pourrait s'apparenter au périmètre d'un objet géometrique tel qu'un cercle, un triangle. Ici on pousse le concept plus loin en généralisant à toutes les fonctions.
La longueur de la représentation graphique de
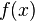
![\displaystyle [ a ; b ]](https://static.techno-science.net/illustration/Definitions/autres/9/98671949dc395183d9e562841c324456_630387f599fd12a85b33ac979bef7fcb.png)