Samedi 3 Mai 2025
Rechercher 🔍

Groupe des classes d'idéaux - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Histoire et origine du groupe des classes d'idéaux - Exemples de groupes des classes d'idéaux - Développement technique - Démonstrations - Principe de la méthode - Connexions avec la théorie des corps de classes

Démonstrations

Décors

Le cas illustré est celui où K = Q [√17]. La figure représente KR. Ici r1 est égal à 2 et r2 à 0. Les points gris sont les images de l'anneau des entiers par Σ. Ils sont tous combinaisons linéaires à coefficients entiers des images de 1 et ω = 1/2(1 + √17). La zone bleue est celle contenant les points d'image inférieure à 4 par NR.

Ici Q désigne le corps des nombres rationnels, K une extension finie de Q de degré d et C le corps des nombres complexes. L'anneau étudié, noté OK est la fermeture intégrale de K, c'est-à-dire l'ensemble des entiers algébriques contenu dans K. C'est un anneau de Dedekind et tout idéal se décompose de manière unique en un produit d'idéaux premiers. Ce résultat s'obtient en adjoignant des idéaux alors appelés fractionnaires, pour obtenir une structure de groupe. Ces propriétés sont analysées dans l'article détaillé.

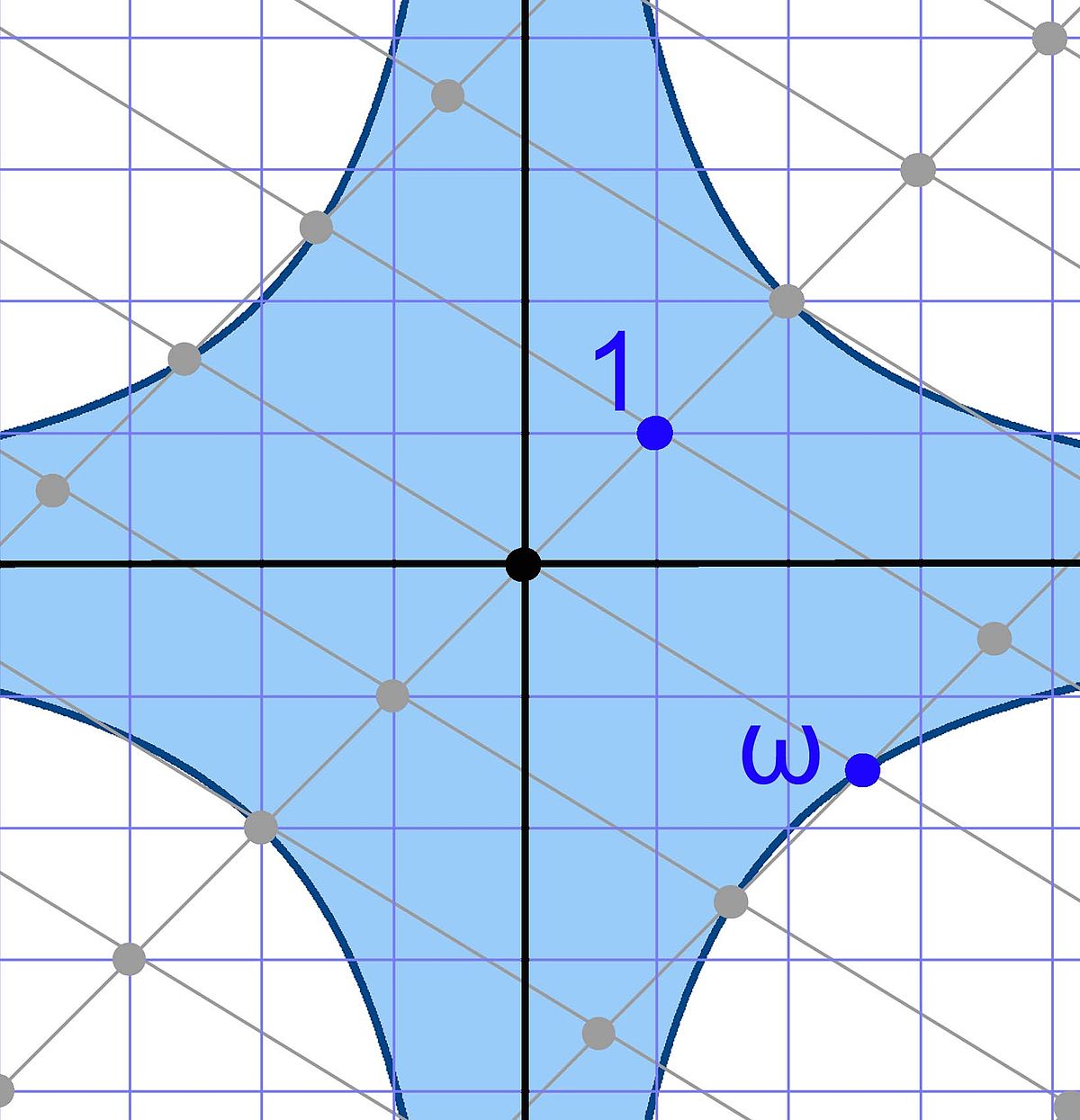
K admet un élément primitif noté ici ζ, c'est-à-dire un nombre tel que tout élément de K s'exprime comme combinaison linéaire des puissance de ζ, à coefficients dans Q. Son polynôme minimal P(X) est par définition irréductible. Dans ce contexte, K est le corps de rupture de ζ, ce qui signifie que l'on peut considérer K comme le quotient de l'anneau des polynômes Q[X] par l'idéal maximal engendré par P(X). L'élément ζ est alors exactement égal à la classe de X dans K. Le polynôme P(X) n'admet pas de racine multiple car il est irréductible (cf corps parfait). Considéré comme un polynôme à valeurs dans C, P(X) admet d différentes racines si d est la dimension de K, ou encore le degré de P(X). Il existe d plongements de K dans C, le terme plongement désigne ici un morphisme de corps, nécessairement injectif. Chaque plongement associe à ζ une racine du polynôme P(X). Si, par exemple le polynôme P(X) est égal à X3 - 2, alors les différentes images possibles de ζ sont 21/3, j.21/3 et jc.21/3, ici j désigne la racine cubique de l'unité à composante imaginaire strictement positive et l'indice c, appliqué à un nombre complexe, son conjugué. On note σ1, ..., σd les d différents plongements de K dans C.

Il est déjà possible de remarquer que ces plongements ne sont pas tous de même nature. Si l'image de ζ est réelle, alors le plongement est à valeur dans R. Si elle est complexe alors il existe un autre plongement qui associe à ζ le complexe conjugué. La nature de ses plongements modifie le comportement de la norme, si le plongement est à valeurs complexes, on se retrouve dans une configuration analogue au premier cas étudié dans le paragraphe Principe de la méthode. S'il est à valeurs réelles, c'est le deuxième cas.

Comme, pour chaque plongement à valeurs complexes l'application conjuguée est aussi un plongement, le nombre de plongements complexes est paire. On note r1 le nombre de plongements réels et 2.r2 le nombre de plongements complexes. On ordonne l'indexation des plongements de la manière suivante : si i varie entre 1 et r1, le plongement est réel, puis, le plongement d'indice r1 + j si j varie de 1 à r2 possède comme conjugué r1 + r2 + j.

L'ensemble KR désigne l'espace vectoriel Rr1 x Cr2 et Σ le morphisme de Q algèbre suivant :

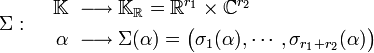
\Sigma : \quad \begin{align}\mathbb K \ & \longrightarrow \mathbb K_{\mathbb R} = \mathbb R^{r_1} \times \mathbb C^{r_2} \\ \alpha \ & \longrightarrow \Sigma(\alpha)= \big(\sigma_1(\alpha),\cdots ,\sigma_{r_1 + r_2}(\alpha)\big) \end{align}

On définit de même une fonction NR de KR à valeur dans R par :

\mathcal N_{\mathbb R} : \quad \begin{align}\mathbb K_{\mathbb R} \ & \longrightarrow \mathbb R \\ x \ & \longrightarrow \mathcal N_{\mathbb R}(x)= |x_1|\cdot \; \cdots \; \cdot |x_{r_1}|\cdot |x_{r_1 +1}|^2\cdot \;\cdots \; \cdot |x_{r_1 + r_2}|^2 \end{align} \quad \text{avec}\quad x =(x_1,\cdots,x_{r_1 + r_2})

La norme NR correspond à la moyenne géométrique des différentes valeurs absolues ou modules si la coordonnée est complexe.

Si NK désigne la fonction qui à un élément α de K associe sa norme relative élément de Q, on obtient le diagramme commutatif :

\begin{matrix} & \mathbb K & \xrightarrow{\Sigma} & \mathbb K_{\mathbb R} \\ \mathcal N_{\mathbb K /\mathbb Q} & \downarrow & & \downarrow & \mathcal N_{\mathbb R} \\ & \mathbb Q & \xrightarrow{|\cdot |} & \mathbb R \end{matrix}

En effet, la norme arithmétique d'un élément de K est égale au coefficient constant de son polynôme minimal, autrement dit au produit de toutes le racines de son polynôme minimal, s'il est considéré comme à valeurs complexes. On munit KR de la norme géométrique suivante :

\|\cdot\| : \quad \begin{align}\mathbb K_{\mathbb R} \ & \longrightarrow \mathbb R_+ \\ x \ & \longrightarrow \|x\|= |x_1| + \cdots + |x_{r_1}| + 2|x_{r_1 +1}|+\cdots +2|x_{r_1 + r_2}| \end{align}

Le rôle du coefficient 2 apparaît clair dans le cas des entiers quadratiques, le domaine fondamental d'un idéal y est égal à son discriminant si l'anneau est totalement réel (les éléments du groupe de Galois sont à valeur dans R) et à la moitié du discriminant sinon. Le coefficient 2 permet ici d'obtenir une relation simple entre le volume fondamental et le discriminant d'un idéal.

Le discriminant d'une forme bilinéaire dans un Z-module sur un anneau correspond au déterminant d'une matrice qui la représente. Comme les endomorphismes inversibles ont un déterminant aussi inversible et donc égal à +/-1, un changement de base ne modifie pas le discriminant. Ce terme est aussi appliqué à un anneau d'entiers algébriques ou à un idéal de l'anneau. La forme bilinéaire associé donne pour valeur du couple (a, b) la trace de l'application linéaire qui à x associe a.b.x, elle porte le nom de forme trace.

Lemmes techniques

  • La majoration suivante est toujours vérifiée :
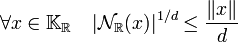
\forall x \in \mathbb K_{\mathbb R}\quad |\mathcal N_{\mathbb R}(x)|^{1/d}\le \frac{\|x\|}d

Ce lemme signifie simplement que la moyenne géométrique est plus petite que la moyenne arithmétique.

Soit δ une longueur, c'est-à-dire un nombre réel positif :

  • Le volume V d'une boule de KR de rayon δ est donné par la formule suivante :
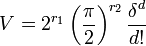
V = 2^{r_1}\left(\frac{\pi}2 \right)^{r_2} \frac {\delta^d}{d!}

Considérons l'image de OK dans KR, c'est un Z module. Son volume fondamental est la mesure de l'aire composée par l'ensemble des vecteurs de coordonnées toutes prises dans l'intervalle [0, 1[ si la base choisie est une base du module. Comme tout isomorphisme de Z module possède un déterminant inversible dans Z, l'isomorphisme possède un déterminant égal à +/- 1. Ainsi le volume fondamental est indépendant du choix de la base du module. Ce volume correspond à celui de KR/ Σ(OK). Pour cette raison, on le note Vol (KR/ Σ(OK)). Le troisième lemme technique concerne un volume de cette nature :

  • Soit M un idéal de OK, l'égalité suivante est vérifiée :
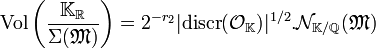
\text{Vol}\left(\frac {\mathbb K_{\mathbb R}}{\Sigma (\mathfrak M)}\right) = 2^{-r_2}|\text{discr}(\mathcal O_{\mathbb K})|^{1/2}.\mathcal N_{\mathbb K/\mathbb Q}(\mathfrak M)

La fonction Σ est celle définie au paragraphe précédent.

  • La majoration suivante est toujours vérifiée :
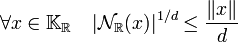
\forall x \in \mathbb K_{\mathbb R}\quad |\mathcal N_{\mathbb R}(x)|^{1/d}\le \frac{\|x\|}d
Convex Function.svg

Cette propriété est une conséquence de la convexité de la fonction exponentielle. Si ai désigne la valeur absolue ou le module de xi, la majoration à démontrer est la suivante :

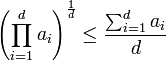
\left(\prod_{i=1}^d a_i\right)^{\frac 1d}\le \frac {\sum_{i=1}^d a_i}d

Pour pouvoir utiliser les propriétés de convexité de l'exponentielle, on utilise les propriétés du logarithme :

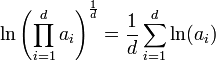
\ln\left(\prod_{i=1}^d a_i\right)^{\frac 1d}=\frac 1d\sum_{i=1}^d \ln(a_i)

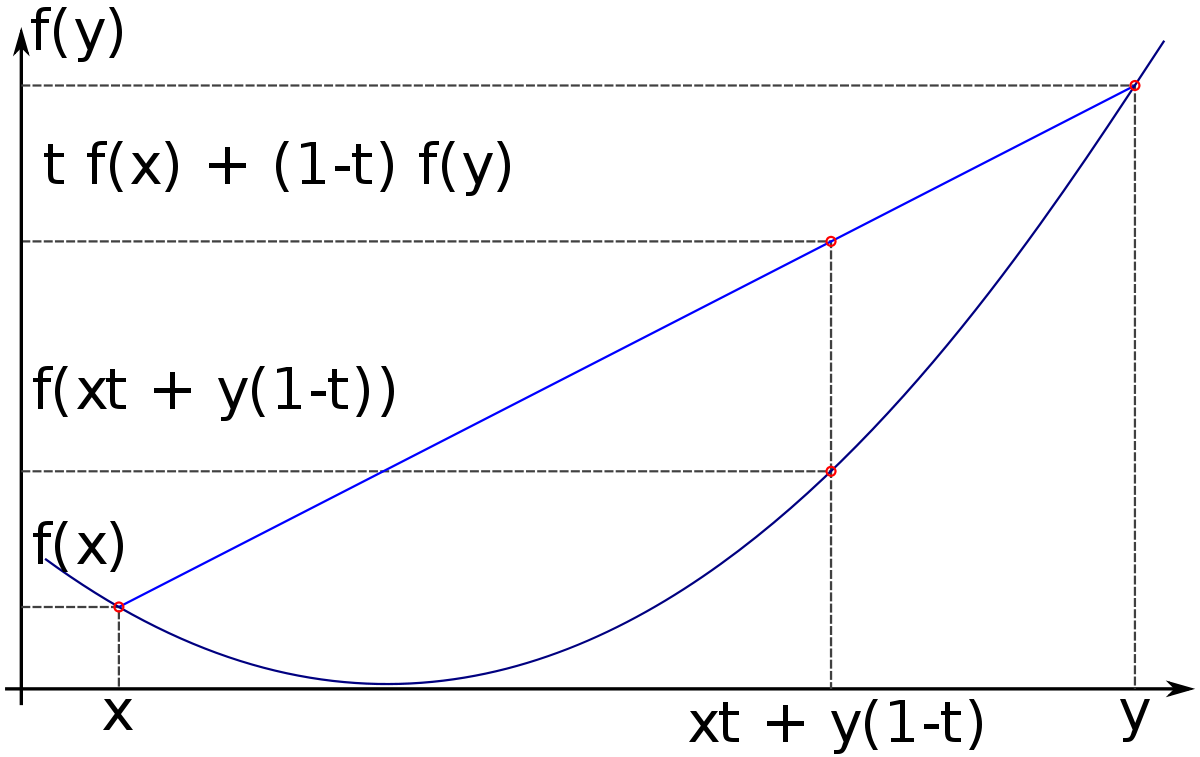
Toute fonction convexe possède la propriété illustrée à droite : l'image du barycentre par la fonction convexe est plus petite que le barycentre des images. Le coefficient du barycentre, t sur la figure, est choisi entre 0 et 1. Cette propriété est vraie pour deux points, mais aussi pour d points. La convexité de l'exponentielle permet de conclure :

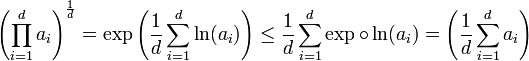
\left(\prod_{i=1}^d a_i\right)^{\frac 1d} = \exp\left(\frac 1d\sum_{i=1}^d \ln(a_i)\right) \le \frac 1d \sum_{i=1}^d \exp \circ \ln(a_i) = \left(\frac 1d\sum_{i=1}^d a_i\right)

On remarque que si l'un des coefficients ai est nul, la démonstration n'est plus valable. Cependant, si ai est nul, le terme de gauche est nul et celui de droite positif, la majoration est bien vérifiée.

  • Le volume V d'une boule de KR de rayon δ est donné par la formule suivante :
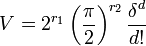
V = 2^{r_1}\left(\frac{\pi}2 \right)^{r_2} \frac {\delta^d}{d!}

Le calcul est le fruit d'une double récurrence, d'abord sur r1 puis sur r2. Notons Vλμδ le volume de la sphère si r1 est égal à λ et r2 à μ et le rayon δ.

Intégrale d'une pyramide.jpg
  • L'égalité suivante est vérifiée :
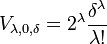
V_{\lambda,0,\delta} = 2^{\lambda}\frac {\delta^{\lambda}}{\lambda!}

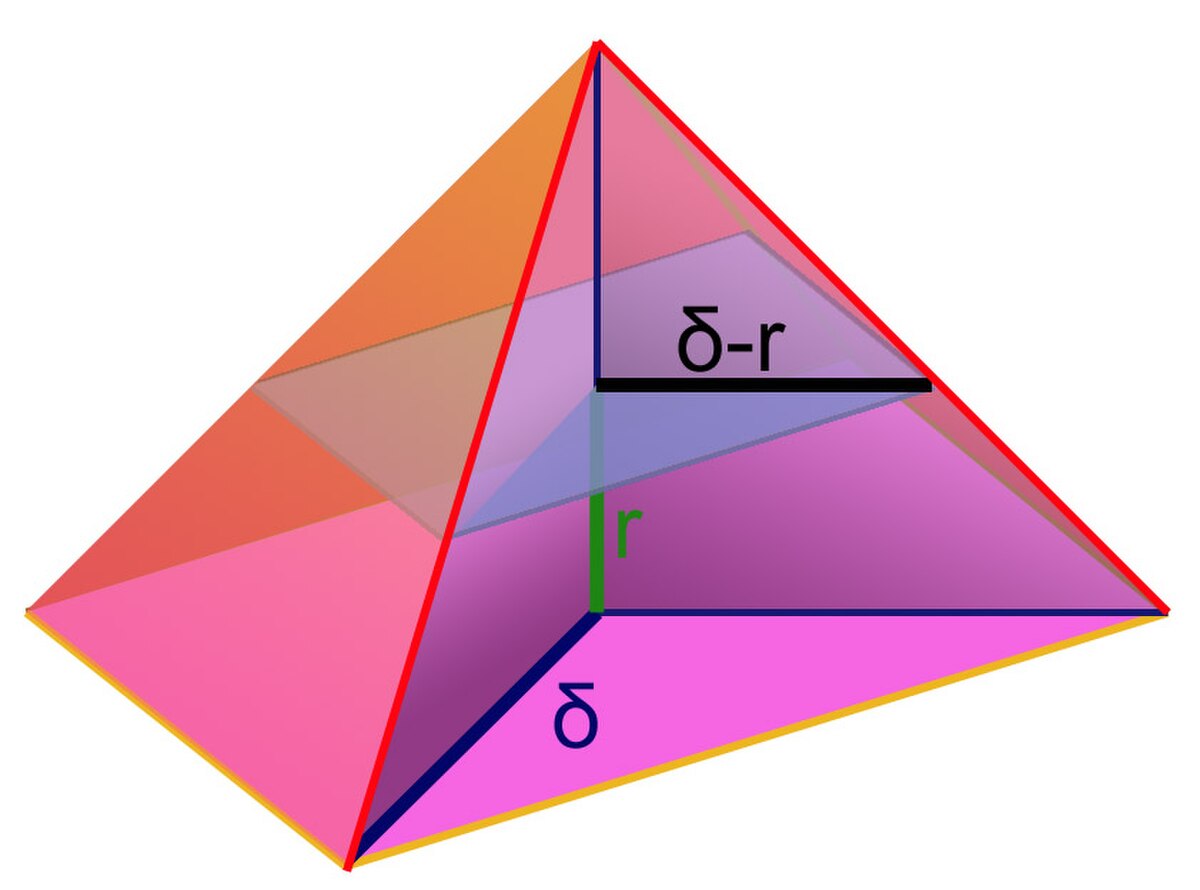
La boule ressemble, en dimension d à un dé à 2d faces. En dimension 3 elle est composée de deux pyramides dont la moitié est représentée sur la figure de droite. Si λ est égal à 1, l'égalité est vérifiée, en effet :

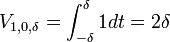
V_{1,0,\delta} =\int_{-\delta}^\delta 1 dt = 2\delta

Ce calcul revient à dire qu'un segment de rayon δ est de longueur 2δ. Supposons maintenant établie la proposition pour λ - 1 et montrons là pour λ. L'intégrale utilisée est celle illustrée sur la figure. On ne calcule que la moitié supérieure, car le volume de la moitié inférieure est le même. L'intégrale est sur la variable r, qui varie de 0 à δ. La section obtenue en coupant la boule par l'hyperplan des points de première coordonnée égale à r correspond à la zone bleue. Son volume est égal à Vλ- 1,0,δ-r. On en déduit :

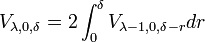
V_{\lambda,0,\delta} =2\int_{0}^\delta V_{\lambda - 1,0,\delta -r} dr

Avec me changement de variable t = δ - r, on obtient :

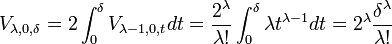
V_{\lambda,0,\delta} =2\int_{0}^\delta V_{\lambda - 1,0,t}dt= \frac {2^{\lambda}}{\lambda!}\int_0^\delta \lambda t^{\lambda -1}dt = 2^{\lambda}\frac {\delta^{\lambda}}{\lambda!}

Il suffit alors de traiter le cas complexe :

Intégrale d'un cone.jpg
  • L'égalité suivante est vérifiée :
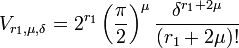
V_{r_1,\mu,\delta} = 2^{r_1}\left(\frac{\pi}2 \right)^{\mu} \frac {\delta^{r_1+2\mu}}{(r_1 + 2\mu)!}

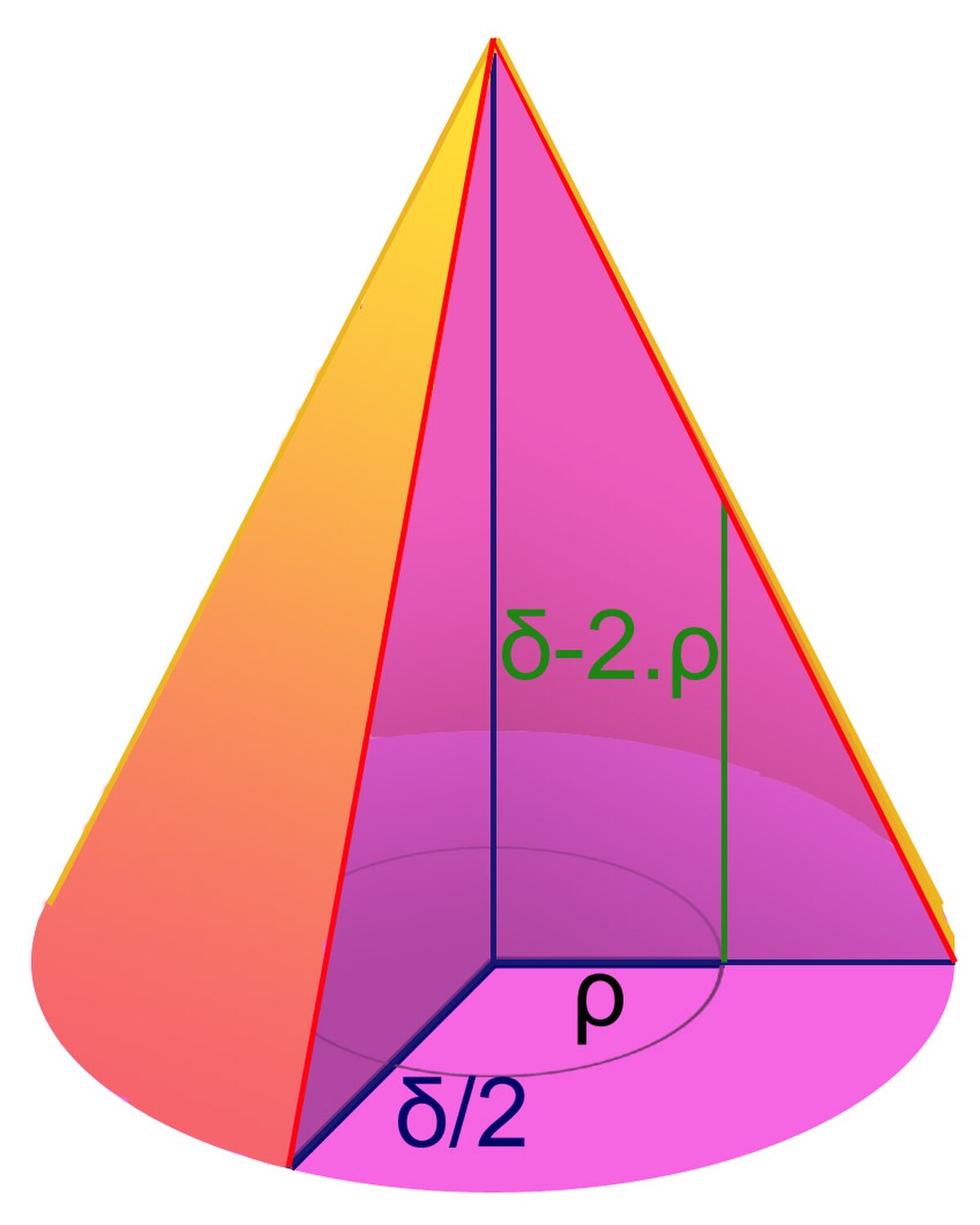
Cette fois ci, on ajoute des disques à la boule. En dimension 3, si r1 et r2 sont égaux à 1, la partie supérieure correspond à la figure de droite. Le cercle est de rayon δ/2 car il existe un coefficient 2 devant les termes complexes. Une telle configuration laisse penser à un usage de coordonnées polaires ρ et θ. On procède encore par récurrence.

Si μ est égal à 0, les calculs précédents établissent le résultat. Supposons le résultat vrai à l'ordre μ - 1 et montrons le pour μ.

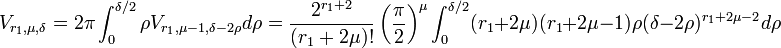
V_{r_1,\mu,\delta}=2\pi\int_0^{\delta/2} \rho V_{r_1,\mu -1,\delta - 2\rho}d\rho = \frac{2^{r_1+2}}{(r_1 + 2\mu)!} \left(\frac{\pi}2 \right)^{\mu}\int_0^{\delta /2} (r_1 + 2\mu)(r_1 + 2\mu-1)\rho(\delta - 2\rho)^{r_1+2\mu -2} d\rho

Comme précédemment, on pose le changement de variable t = δ - 2.ρ :

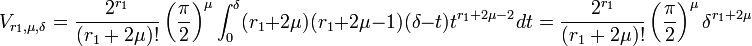
V_{r_1,\mu,\delta}=\frac{2^{r_1}}{(r_1 + 2\mu)!}\left(\frac{\pi}2 \right)^{\mu}\int_0^{\delta}(r_1 + 2\mu)(r_1 + 2\mu-1)(\delta - t)t^{r_1+2\mu -2} dt = \frac{2^{r_1}}{(r_1 + 2\mu)!}\left(\frac{\pi}2 \right)^{\mu}\delta^{r_1+2\mu}

Ce qui démontre la proposition.

  • Soit M un idéal de OK, l'égalité suivante est vérifiée :
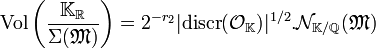
\text{Vol}\left(\frac {\mathbb K_{\mathbb R}}{\Sigma (\mathfrak M)}\right) = 2^{-r_2}|\text{discr}(\mathcal O_{\mathbb K})|^{1/2}.\mathcal N_{\mathbb K/\mathbb Q}(\mathfrak M)

Soit B égale à (bi) pour i variant de 1 à d une base de OK. Etablissons dans un premier temps le volume fondamental de Σ(OK). Il est égal au déterminant suivant :

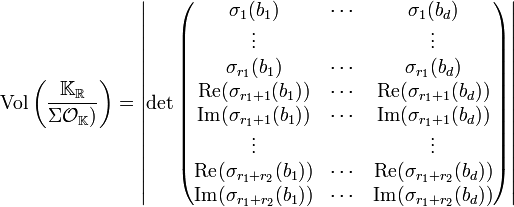
\text{Vol}\left(\frac {\mathbb K_{\mathbb R}}{\Sigma \mathcal O_{\mathbb K})}\right) = \left| \det \begin{pmatrix} \sigma_1(b_1) & \cdots & \sigma_1(b_d) \\ \vdots & & \vdots \\ \sigma_{r_1}(b_1) & \cdots & \sigma_{r_1}(b_d) \\ \text{Re}(\sigma_{r_1+1}(b_1)) & \cdots & \text{Re}(\sigma_{r_1+1}(b_d)) \\ \text{Im}(\sigma_{r_1+1}(b_1)) & \cdots & \text{Im}(\sigma_{r_1+1}(b_d)) \\ \vdots & & \vdots \\ \text{Re}(\sigma_{r_1+r_2}(b_1)) & \cdots & \text{Re}(\sigma_{r_1+r_2}(b_d)) \\ \text{Im}(\sigma_{r_1+r_2}(b_1)) & \cdots & \text{Im}(\sigma_{r_1+r_2}(b_d)) \\ \end{pmatrix}\right|

En multipliant à gauche la matrice précédente par une matrice bloc diagonale comportant r1 matrice 1x1 égales à (1) et par r2 matrice 2x2 donnée à la ligne suivante :

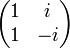
\begin{pmatrix} 1 & i \\ 1 & -i \\ \end{pmatrix}

On obtient l'égalité suivante :

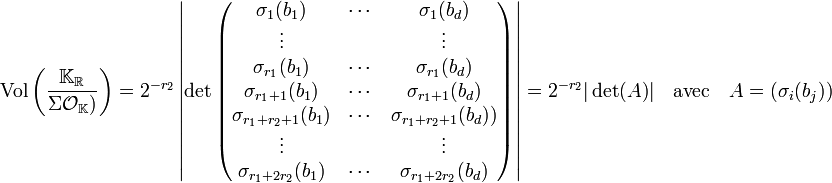
\text{Vol}\left(\frac {\mathbb K_{\mathbb R}}{\Sigma \mathcal O_{\mathbb K})}\right) = 2^{-r_2}\left| \det \begin{pmatrix} \sigma_1(b_1) & \cdots & \sigma_1(b_d) \\ \vdots & & \vdots \\ \sigma_{r_1}(b_1) & \cdots & \sigma_{r_1}(b_d) \\ \sigma_{r_1+1}(b_1) & \cdots & \sigma_{r_1+1}(b_d) \\ \sigma_{r_1+r_2+1}(b_1) & \cdots & \sigma_{{r_1+r_2+1}}(b_d)) \\ \vdots & & \vdots \\ \sigma_{r_1+2r_2}(b_1) & \cdots & \sigma_{r_1+2r_2}(b_d) \\ \end{pmatrix}\right| = 2^{-r_2}|\det(A)| \quad \text{avec}\quad A = (\sigma_i(b_j))

Notons (bij) les coordonnées de la transposée de A. Elle est définie par bij = σj(bi). On a :

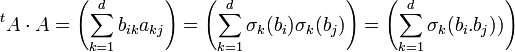
^tA\cdot A =\left(\sum_{k=1}^d b_{ik}a_{kj}\right)=\left(\sum_{k=1}^d \sigma_k(b_i)\sigma_k(b_j)\right)= \left(\sum_{k=1}^d \sigma_k(b_i.b_j))\right)

On reconnait la forme trace, on en déduit :

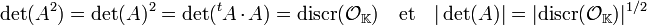
\det (A^2) = \det (A)^2 = \det (^tA\cdot A) = \text{discr}(\mathcal O_{\mathbb K})\quad \text{et}\quad |\det (A)| = |\text{discr}(\mathcal O_{\mathbb K})|^{1/2}

Pour conclure, il suffit d'utiliser l'égalité suivante, démontrée dans l'article Forme trace :

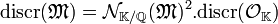
\text{discr}({\mathfrak M}) = \mathcal N_{\mathbb K/\mathbb Q}(\mathfrak M)^2.\text{discr}(\mathcal O_{\mathbb K})\;
 

Théorèmes

Une fois les trois lemmes établis le théorème fondamental :

  • Si l'extension K est finie, le groupe des classes des idéaux de OK est fini.

est relativement simple à démontrer. La preuve utilise le résultat intermédiaire :

  • Si M est un idéal non nul de OK, il existe un élément m de M dont la norme relative vérifie la majoration suivante :
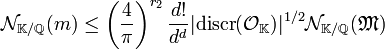
\mathcal N_{\mathbb K/\mathbb Q}(m) \le \left(\frac 4\pi\right)^{r_2} \frac {d!}{d^d}|\text{discr}(\mathcal O_{\mathbb K})|^{1/2} \mathcal N_{\mathbb K/\mathbb Q}(\mathfrak M)

Cette proposition est la conséquence directe du théorème de Minkowski et des lemmes précédents. Elle implique le résultat suivant, conséquence du fait que la norme relative est multiplicative :

  • Soit M un idéal non nul de O, la classe de M -1 contient un idéal de norme inférieure à b, avec b défini par :
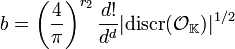
b= \left(\frac 4\pi\right)^{r_2} \frac {d!}{d^d}|\text{discr}(\mathcal O_{\mathbb K})|^{1/2}

La proposition suivante est immédiate :

  • Soit n un entier strictement positif, il n'existe qu'un nombre fini d'idéaux de norme relative n.

Il n'existe en effet qu'un nombre fini d'anneaux unitaires intègres de cardinal n et qu'un nombre fini de morphismes d'anneaux de OK dans un anneau donné.

Le théorème principal est la conséquence des deux derniers résultats. Il permet de démontrer le résultat suivant :

  • L'anneau OK est factoriel si et seulement s'il est principal.
  • Si M est un idéal non nul de OK, il existe un élément m de M dont la norme relative vérifie la majoration suivante :
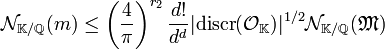
\mathcal N_{\mathbb K/\mathbb Q}(m) \le \left(\frac 4\pi\right)^{r_2} \frac {d!}{d^d}|\text{discr}(\mathcal O_{\mathbb K})|^{1/2} \mathcal N_{\mathbb K/\mathbb Q}(\mathfrak M)

Le théorème de Minskowski indique qu'une boule B( δ) de centre l'origine et de rayon δ contient un élément non nul d'un réseau fondamental de volume v si δ est tel que le volume de la boule B( δ) est supérieur à 2dv. Le réseau qui nous intéresse est Σ(OK), son volume fondamental est le fruit du calcul d'un des lemmes précédents. Le volume de la boule B( δ) est aussi donné par un des lemmes précédents. En conséquence, la boule contient nécessairement un point du réseau Σ(OK) si la majoration suivante est vérifiée :

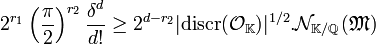
2^{r_1}\left(\frac{\pi}2 \right)^{r_2} \frac {\delta^d}{d!} \ge 2^{d-r_2}|\text{discr}(\mathcal O_{\mathbb K})|^{1/2}.\mathcal N_{\mathbb K/\mathbb Q}(\mathfrak M)

On en déduit que si δ vérifie la majoration suivante, il existe un élément m de l'idéal M dans la boule B( δ)

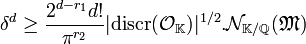
\delta^d \ge \frac {2^{d-r_1}d!}{\pi^{r_2}}|\text{discr}(\mathcal O_{\mathbb K})|^{1/2}.\mathcal N_{\mathbb K/\mathbb Q}(\mathfrak M)

De plus, l'élément m, de la boule B( δ) vérifie, d'après le premier lemme et en remarquant que d - r1 est égal à 2.r2 :

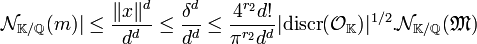
\mathcal N_{\mathbb K/\mathbb Q}(m)|\le\frac{\|x\|^d}{d^d} \le \frac {\delta^d}{d^d}\le \frac {4^{r_2}d!}{\pi^{r_2}d^d}|\text{discr}(\mathcal O_{\mathbb K})|^{1/2}.\mathcal N_{\mathbb K/\mathbb Q}(\mathfrak M)

Ce qui démontre la proposition.

  • Soit M un idéal non nul de O, la classe de M -1 contient un idéal de norme inférieure à b, avec b défini par :
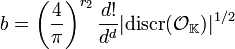
b= \left(\frac 4\pi\right)^{r_2} \frac {d!}{d^d}|\text{discr}(\mathcal O_{\mathbb K})|^{1/2}

Soit m un élément de M dont la norme relative vérifie la majoration de la proposition précédente. Par définition de l'idéal M -1, mM-1 est un idéal noté N de OK appartenant à la même classe que M -1. La multiplicativité des normes et la proposition précédente montrent que :

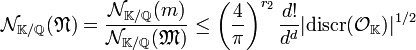
\mathcal N_{\mathbb K/\mathbb Q} (\mathfrak N) = \frac {\mathcal N_{\mathbb K/\mathbb Q} (m)}{\mathcal N_{\mathbb K/\mathbb Q} (\mathfrak M)} \le \left(\frac 4\pi\right)^{r_2} \frac {d!}{d^d}|\text{discr}(\mathcal O_{\mathbb K})|^{1/2}
  • L'anneau OK est factoriel si et seulement s'il est principal :

Tout anneau principal est factoriel. Cette propriété se démontre ici sans appel à l'axiome du choix comme dans la démonstration générale. En effet, soit a un entier de OK, l'idéal aOK se décompose de manière unique en produit d'idéaux premiers. Comme l'anneau est principal, chaque idéal est de la forme piOK où pi est un nombre premier. L'entier a est donc le produit d'une unité (un élément inversible) et de nombres premiers. Comme la décomposition en idéaux premiers est unique, l'anneau est bien factoriel.

Réciproquement, supposons que l'anneau OK soit factoriel. Montrons tout d'abord par contraposée que si p est un nombre premier pOK est un idéal premier. Soit M un idéal premier contenant un nombre premier p. Supposons que p n'engendre pas M, la décomposition en idéaux premiers de pOK contient M, il existe un idéal N produit de tous les autres facteurs de pOK dans sa décomposition en idéaux premiers tel que pOK = M.N. Soit m (resp. n) un élément de M (resp. N) non multiple de p. Un tel élément existe sinon pOK serait égal à M (resp. N). L'élément m.n est un multiple de p, or ni m ni n ne sont des multiples de p et l'anneau OK n'est pas factoriel. On en déduit si l'anneau est factoriel, il n'existe qu'un unique idéal premier contenant p, c'est l'idéal engendré par p.

Il suffit maintenant de montrer que tout idéal premier M contient un nombre premier. Soit m un élément de M, la proposition précédente montre que la décomposition en idéaux premiers de m est une décomposition en idéaux principaux de générateurs des nombres premiers. M contient mOK, il est donc présent dans sa décomposition en idéaux premiers. Comme M est premier, il est égal à un de ses facteurs et il est principal.

 
Développement technique
Principe de la méthode
- Introduction - Histoire et origine du groupe des classes d'idéaux - Exemples de groupes des classes d'idéaux - Développement technique - Démonstrations - Principe de la méthode - Connexions avec la théorie des corps de classes
miniature
La face cachée de la Lune révèle une étrangeté 🌓
miniature
Piéger le CO2 sous terre indéfiniment, c'est possible ! 🌍
miniature
La plus lointaine cousine de la Voie Lactée jamais observée 🌀
miniature
Ce codex médiéval cache un secret dans son bois 🔍
miniature
Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋
miniature
Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️
miniature
Des singularités temporelles dans l'Univers ? 🕰️
miniature
Des fossiles de dinosaures mieux datés 🦖
miniature
Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭
miniature
Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆
miniature
Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜
miniature
Le rôle méconnu de la décharge dans l'usure des batteries 🔋
miniature
1
La fonte des glaces déplace les pôles: quelles conséquences ? 🌍
miniature
L'appareil photo de votre smartphone peut détecter l'antimatière 📱
miniature
Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐
miniature
Un mosasaure géant découvert dans le Mississippi 🦕
miniature
Problème, les galaxies meurent plus tôt que prévu 🌀
miniature
Ce lien entre cannabis et troubles psychotiques 🧠
miniature
Une révolution dans le refroidissement des puces électroniques ? 🔥
miniature
Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀
miniature
Lucy survole un astéroïde en forme de cacahuète 🚀
miniature
Découverte du fossile d'un dinosaure géant méconnu 🦕
miniature
Mars avait-elle un champ magnétique unilatéral ? 🔍
miniature
Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇
miniature
Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁
miniature
L'électroluminescence du graphène, une découverte inattendue ! 💡
miniature
Cet objet métallique n'a pas été fabriqué sur Terre 🔧
miniature
1
Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡
miniature
Cette super-Terre brûle les attentes des astronomes 🔥
miniature
Découverte exceptionnelle de fossiles d'amphibiens géants 🐸
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
Page générée en 0.163 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise