Paradoxe des jumeaux - Définition
Le paradoxe des jumeaux est une expérience de pensée en relativité restreinte imaginée par Paul Langevin en 1911. Langevin n'imagina pas cette expérience pour mettre en défaut la relativité restreinte mais plutôt pour en expliquer certains aspects. Il n'y voyait aucun paradoxe et cette appellation est apocryphe. Cette vision paradoxale n'est apparue que plus tardivement à travers les discussions et interprétations parfois erronées de la relativité restreinte. Nous irons donc dans cet article un peu plus loin que l'analyse initiale de Langevin.
Ce paradoxe a fait couler beaucoup d'encre et reste sans doute un des sujets favoris des amateurs de relativité, bien qu'il ne pose plus aucun problème de contradiction logique, juste un aspect des choses surprenant. On continue cependant, par habitude, à le nommer "paradoxe" encore de nos jours.
Le point de vue de Langevin
Voyons tout d'abord la situation expérimentale qui est envisagée.
Considérons deux frères jumeaux, appelons les Alain et Bernard. Alain reste sur Terre tandis que son frère entame un voyage dans l'espace avec une très grande vitesse, proche de celle de la lumière. Lorsque Bernard revient sur Terre, Alain est maintenant un homme âgé alors que Bernard est resté jeune.
Cela pourrait apparaître comme déjà un paradoxe pour certaines personnes, mais la dilatation du temps était mentionnée par la relativité restreinte depuis déjà 1905. Bernard se déplaçant à grande vitesse, Alain constate que l'horloge de Bernard fonctionne plus lentement que la sienne et donc Bernard vieillit moins vite.
Langevin, dans son article, parle de l'évolution des concepts de l'espace et du temps en physique et présente les principaux aspects de la relativité restreinte.
Il présente en particulier la dilatation du temps. Celle-ci s'applique de manière réciproque à deux observateurs en mouvement relatif uniforme (vitesse relative constante). Toutefois ce raisonnement peut aussi s'appliquer si un des observateurs est accéléré. Pendant un intervalle de temps infinitésimal, la vitesse peut être considérée comme constante et la dilatation du temps peut être utilisée. À l'aide de ce raisonnement il montre que le temps propre est toujours plus court pour un objet accéléré que pour un objet inertiel.
Langevin utilise l'expérience avec les jumeaux pour illustrer ce phénomène. Un des jumeaux étant accéléré, son temps propre sera plus court que celui de son frère resté sur Terre.
L'analyse de Langevin peut laisser croire que l'absence de vieillissement est due à l'accélération proprement dite. Mais ce n'est pas le cas. Il raisonne, pour appliquer la dilatation du temps, sur des intervalles infinitésimaux et l'accélération est seulement responsable de la trajectoire "fermée" du jumeau voyageur, lui permettant de revenir auprès de son frère.
L'accélération est donc seulement une cause de dissymétrie. Elle implique que les deux jumeaux sont dans une situation différente. Langevin explique la différence entre le mouvement uniforme, qui est relatif, et le mouvement accéléré, qui a un caractère absolu comme le montre l'existence d'effets physiques (par exemple, les charges électriques accélérées émettent un rayonnement électromagnétique).
Langevin aborde aussi l'explication Doppler, montrant clairement la dissymétrie.
Le "paradoxe moderne"
Peu de temps après la publication de l'article de Langevin, l'expérience qu'il avait imaginée entraîna de nombreux commentaires et des analyses parfois erronées. C'est à cette occasion que le paradoxe prit sa forme moderne que nous lui connaissons. C'est sous cette forme que nous allons le présenter et l'étudier.
La relativité restreinte affirme qu'il n'y a pas de repère absolu. Deux repères en mouvement relatif à vitesse constante sont totalement équivalents. Qu'est-ce qui nous autorise à affirmer que c'est Bernard qui s'éloigne d'Alain et pas l'inverse ? Du point de vue de Bernard, la situation est différente. C'est Alain qui se déplace à grande vitesse et qui parcourt un long chemin avant de le retrouver.
La dilatation du temps est parfaitement réciproque en relativité restreinte. Ainsi Bernard doit lui aussi constater que l'horloge d'Alain fonctionne plus lentement. Et lors de leurs retrouvailles, c'est donc, de son point de vue, Alain qui devrait être resté jeune.
Pourtant, une fois qu'ils sont à nouveau ensemble ils doivent être d'accord dans la comparaison de leur âge. La comparaison de deux horloges situées au même point est même une des clefs de la synchronisation en relativité restreinte. Ce n'est que lorsque deux événements se produisent au même point et au même moment qu'on peut être certain sans équivoque de leur simultanéité. Or Alain ne peut être à la fois plus jeune et plus vieux que Bernard.
Nous avons là un paradoxe. Lorsque Einstein a posé le principe de relativité, il a eu une des intuitions certainement parmi les plus remarquables de la physique moderne. Et la symétrie invoquée ci-dessus en est une des conséquences. Aurait-il commis une erreur ? N'y a-t-il pas là, un paradoxe évident ? Une contradiction flagrante ?
Le point de vue de Langevin que nous avons évoqué plus haut apporte déjà des éléments de réponse. Mais il reste que l'on a du mal à voir comment une accélération se produisant pendant un temps aussi bref pourrait avoir une telle influence.
On pourrait se demander pourquoi c'est justement le repère d'Alain qui est inertiel et pas celui de Bernard. En somme, d'où vient ce caractère absolu des accélérations ? Einstein évoque cette question dans son article de 1918 où il admet que la relativité restreinte évite ce problème en postulant sans autre explication l'existence de ces repères inertiels. Il pensait que seule la relativité générale apportait une réponse satisfaisante au paradoxe; puis a abandonné cette idée.
Il n'est nullement besoin de faire intervenir la relativité générale pour résoudre le paradoxe de Langevin. Mais nous aborderons tout de même celle-ci pour discuter de cette problématique de la classe des repères inertiels mais aussi pour discuter de certaines variantes du paradoxe faisant intervenir la gravitation.
Contexte
Le paradoxe utilise la dilatation du temps prévue par la relativité restreinte pour un système en mouvement.
Celle-ci s'est toujours vérifiée expérimentalement :
- De nos jours, les particules instables se désintègrent plus lentement du point de vue de l'observateur lorsqu'elles se meuvent à grande vitesse par rapport à celui-ci, notamment dans les accélérateurs de particules.
- Cet effet est également observé pour les muons atmosphériques produits par la collision des rayons cosmiques (particules très énergétiques émises en particulier par le soleil) et les molécules de l'atmosphère. Ces muons, animés de grandes vitesses, atteignent le sol où ils sont observés et ce malgré leur courte durée de vie, la dilatation du temps leur donnant le temps nécessaire pour atteindre les détecteurs.
- Un autre cas observé de dilatation temporelle est le décalage entre horloges atomiques au sol et en vol ; mais il se complique dans ce dernier cas de considérations gravitationnelles, et nous sortons alors du cadre de la relativité restreinte. Il est remarquable que l'expérience réelle des horloges atomiques embarquées en avion (ou en train, ou en voiture...) ou qui restent fixées au sol est une version réalisable, et souvent réalisée de l'expérience des jumeaux, où l'on remplace simplement le vaisseau spatial par un avion, et un être humain par une horloge atomique. On mesure ensuite la différence des durées mesurées par les horloges.
- Signalons également que l'on observe aussi cette dilatation du temps sur la durée des courbes de luminosités des supernovae lointaines. Cette dilatation du temps correspondant à la vitesse de récession également observée grâce à l'effet Doppler.
Résolution
Il existe plusieurs manières d'expliquer le paradoxe des jumeaux. Ces explications ne sont pas toujours mutuellement exclusives et ne correspondent pas nécessairement à différentes théories. Ce sont simplement des manières différentes d'expliquer le même phénomène et elles apportent plusieurs éclairages sur divers aspects important de la relativité restreinte.
Pour bien appréhender ce qui se passe, il est donc utile de voir le problème sous différentes facettes. Et en tout premier lieu de voir ce qui est erroné dans le raisonnement ci-dessus entraînant le paradoxe.
Dilatation du temps et erreur de raisonnement
Pour comprendre où est l'erreur de raisonnement il faut bien comprendre les conditions dans lesquelles on peut appliquer les formules de la relativité restreinte.
Ainsi, la dilatation du temps ou les transformations de Lorentz (dont la dilatation du temps est une conséquence) sont établies en supposant que la vitesse relative des repères est uniforme. C'est-à-dire constante en grandeur et en direction ou encore en l'absence d'accélération relative.
Or dans la situation concernée, Bernard est amené à un moment ou un autre à faire demi-tour. Lors de ce demi-tour il doit subir une accélération (ou, puisque la situation est symétrique, Alain subit une accélération du point de vue de Bernard).
La relativité restreinte est construite sur le principe de relativité restreint qui affirme l'équivalence de tous les repères inertiels (ou galiléens). Deux repères inertiels ne différant que par leur vitesse relative uniforme (et éventuellement par l'orientation des axes des repères). Alors que le principe de relativité généralisé, l'équivalence de tous les repères, sans exception, y compris accéléré, nécessite de généraliser la relativité et en particulier les transformations de Lorentz ne sont plus, dans ce cas, valables que localement (dans un voisinage d'espace-temps infinitésimal des événements).
Notons que cela n'implique pas que la relativité restreinte ne puisse pas être appliquée ici. Il convient juste d'être prudent. La restriction porte sur le mouvement relatif de deux repères. Rien n'interdit d'étudier le mouvement d'un corps accéléré (Bernard) dans un repère inertiel (considéré comme étant celui d'Alain).
On ne peut donc considérer les transformations de Lorentz entre les deux repères d'Alain et Bernard ni considérer la dilatation du temps du point de vue du repère non inertiel de Bernard. Nous avons trouvé l'erreur de raisonnement qui induit le paradoxe.
La solution en relativité restreinte
Pour résoudre le problème, il suffit donc de se placer dans le repère inertiel d'Alain (celui qui est resté sur terre) et d'appliquer ce que l'on sait de la relativité restreinte. On peut par exemple tracer les trajectoires :
L'axe vertical représente le temps et l'axe horizontal, spatial, représente la distance parcourue par Bernard dans le repère d'Alain.
Pour connaître le temps écoulé pour chacun des protagonistes, c’est-à-dire leur âge, il suffit de considérer leur temps propre.
Pour Alain, c'est très facile car il est immobile dans son repère. Sa trajectoire est donc une droite verticale (en rouge) dans le diagramme et le temps écoulé pour lui est égal à T.
Pour Bernard, qui effectue un voyage lointain, sa trajectoire est une ligne brisée (en bleu). Quel est son temps propre ? Ce n'est évidemment pas T comme pourrait le laisser croire le diagramme. N'oublions pas que l'espace-temps en relativité restreinte n'est pas euclidien (comme la feuille de papier sur laquelle serait tracé ce diagramme) mais de Minkowski. On voit que sa trajectoire est proche de celle des rayons lumineux (en jaune) et l'on sait que sur des trajectoires de type lumière, le temps propre y est nul. Bernard mesure son temps propre avec son horloge embarquée et il doit être calculé en utilisant les relations de la relativité restreinte.
Ici c'est simple car sa vitesse est constante (en grandeur) et on peut donc appliquer sans crainte la dilatation du temps dans le repère inertiel d'Alain. Le temps écoulé pour Bernard est donc donné par la relation bien connue :
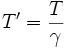
Où γ est le facteur relativiste dépendant de la vitesse de Bernard.
Dans le cas où la trajectoire de Bernard serait quelconque, le calcul se généralise facilement en intégrant le temps propre.
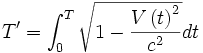
Où
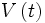
Cette façon de procéder est cohérente avec l'affirmation plus haut que les transformations de Lorentz ne peuvent être considérées comme correctes en présence d'accélérations que pendant une durée infinitésimale et une intégration sur des durées finies est donc inévitable.
L'explication Doppler
Mais que voient Alain et Bernard durant le périple de ce dernier ?
Imaginons par exemple qu'Alain braque un télescope sur Bernard pour voir la manière dont celui-ci vieillit et réciproquement. On peut par exemple imaginer qu'Alain et Bernard disposent d'un émetteur envoyant un train d'impulsions émis à destination de leur frère ou encore tout simplement une liaison vidéo (le voyage dans le futur des autres). Ce dernier recevant le signal a alors une mesure immédiate de la manière dont la fréquence d'émission est affectée par le mouvement et donc du temps qui s'écoule pour l'autre.
Deux effets vont se conjuguer dans cette mesure. Tout d'abord nous avons la dilatation du temps, réciproque (tout au moins tant que la vitesse de Bernard est constante, sans considérer le demi-tour). Ensuite, comme (par exemple), Bernard fuit (puis rattrape) le train d'onde, il observe également un décalage apparent de la fréquence dû au mouvement relatif, dépendant du signe de la vitesse et qui n'est autre que l'effet Doppler.
La conjugaison des deux donne l'effet Doppler relativiste.
Considérons le point de vue de Bernard.
- Initialement Bernard s'éloigne d'Alain. Il observe donc un train d'impulsions dont la fréquence est plus faible. Pour lui, Alain vieillit moins vite.
- Au retour, il s'approche de la source et observe donc un train d'impulsions dont la fréquence est plus élevée. Pour lui, Alain vieillit plus vite.
- La transition se produit lorsqu'il fait demi-tour. Immédiatement, les signaux qui lui parviennent voient leur fréquence varier brusquement.
Du point de vue d'Alain :
- Lorsque Bernard s'éloigne, Alain observe une diminution de la fréquence et Bernard vieillit moins vite.
- Lorsque Bernard se rapproche, Alain observe une augmentation de la fréquence et Bernard vieillit plus vite.
- La transition se produit au moment où Bernard fait demi-tour. Les signaux qu'il envoie subissent donc, lorsqu'ils sont reçus par Alain, une variation brusque de la fréquence.
Mais la situation semble symétrique. Où est la différence ? Simplement lors de la transition. Lorsque Bernard fait demi-tour, cela inverse le sens de l'effet Doppler. Mais Bernard perçoit immédiatement ce changement (c'est lui qui fait demi-tour). Tandis qu'Alain ne le constate pas immédiatement ! Il faut du temps pour que les signaux émis par Bernard parviennent jusqu'à lui. Cela provoque un décalage important.
Ce phénomène est clair lorsque l'on regarde les diagrammes espace-temps fait pour une valeur gamma de 1.5, soit une vitesse pour Bernard de 0.745c.
Où la partie gauche montre les signaux envoyés par Alain à Bernard et la partie droite les signaux envoyés par Bernard à Alain. On voit clairement que la période pendant laquelle Alain constate une fréquence plus élevée est très courte alors que pour Bernard les deux périodes sont équivalentes.
Le calcul redonne bien entendu le même résultat que précédemment.
Notons que ces signaux ne sont nullement nécessaires pour que le phénomène existe. La relativité restreinte elle-même ne nécessite pas que la lumière existe ! Bien que cette dernière soit d'une indéniable utilité pratique aussi bien dans les expériences de pensée que dans les expériences réelles. C'est justement le cas ici où elle permet d'illustrer le phénomène en raisonnant sur ce que voient les jumeaux. Elle a eu aussi un rôle historique primordial dans la genèse de la relativité. Mais ce qui importe en relativité restreinte est l'existence d'une vitesse limite c invariante.
Sans cette vitesse limite, on retrouve la physique classique de Galilée et de Newton. En particulier, la dilatation du temps disparaît et l'effet Doppler relativiste devient l'effet Doppler classique. L'expérience pourrait, par exemple, être faite avec des signaux sonores et des vitesses forcément très petites par rapport à la vitesse de la lumière (plus petites que la vitesse du son), auquel cas les effets relativistes sont négligeables. Et bien que le raisonnement ci-dessus reste valable, le calcul montre (on s'en serait douté) qu'aucune différence d'âge n'est observée au retour.
Tout est dû aux effets relativistes, à la dilatation du temps. Et le raisonnement ci-dessus est donc surtout utile pour bien montrer l'asymétrie du phénomène.
Simultanéité et synchronisation
L'inconvénient de la méthode est qu'elle montre justement ce que "voient" les jumeaux et pas ce qui se passe "réellement". On sait qu'en relativité restreinte, le temps dans deux repères est obtenu à l'aide d'un protocole tenant compte de la vitesse des signaux. Que se passe-t-il si Alain et Bernard tiennent compte, dans leur observation des trains d'impulsion, du temps que ces signaux ont mis pour parvenir jusqu'à eux ?
Dans ce cas, le temps qu'ils mesurent est celui des horloges de leur repère tel que défini en relativité et des temps identiques en deux endroits différents correspondent à des évènements simultanés. Nous savons que la simultanéité est relative et donc que cela pourrait aussi expliquer le phénomène.
Il est donc intéressant de tracer les lignes de simultanéité dans les diagrammes espace-temps. C’est-à-dire les lignes correspondant à des évènements se produisant au même moment. Cela permet de suivre la trajectoire des deux jumeaux "en même temps", du point de vue d'Alain et du point de vue de Bernard.
Les lignes de simultanéité sont simplement les lignes à t constant. C’est-à-dire des lignes horizontales. Les deux protagonistes évoluent donc de concert dans le diagramme, Alain constate une dilatation du temps de Bernard et on retrouve le résultat obtenu plus haut. C'est en fait la même explication !
Pour trouver les lignes de simultanéités de Bernard dans le diagramme d'Alain, il suffit d'utiliser, par exemple, les transformations de Lorentz. À t' constant, on regarde comment varie t en fonction de x.
On constate que les lignes de simultanéité de Bernard sont inclinées. Que se passe-t-il donc du point de vue de Bernard ?
- Initialement, Bernard s'éloigne et il constate que le temps d'Alain évolue plus lentement (dilatation du temps), ce n'est évidemment plus ici un effet apparent comme dans le cas de l'effet Doppler.
- A la fin aussi il constate qu'Alain vieillit plus lentement que lui. Sur la petite portion du diagramme où les lignes de simultanéité joignent la trajectoire d'Alain à la sienne.
- Mais pendant le demi-tour ? On constate qu'il y a un "trou" dans les lignes de simultanéité. Toute une partie de la trajectoire d'Alain n'est pas reliée à celle de Bernard.
On appelle parfois ce "trou" un "Time Gap". Lorsque Bernard fait demi-tour, il change de repère inertiel (il passe d'un repère inertiel dont la vitesse est vers la droite du diagramme à un repère dont la vitesse est vers la gauche). On dit parfois qu'il "saute" de repère ou de référentiel (le repère qui lui est attaché). D'où l'affirmation que lors du saut de référentiel il y a un Time Gap, c’est-à-dire un brusque vieillissement d'Alain du point de vue de Bernard.
Ce Time Gap est dû au changement brutal de la synchronisation. Appelons R le repère inertiel d'Alain. R' le repère inertiel de Bernard s'éloignant vers la droite et R'' celui se dirigeant vers la gauche.
Les protocoles de synchronisation permettent de synchroniser les horloges entre R et R' ainsi qu'entre R et R''. Si l'on considère à un moment donné un point précis, les horloges situées dans R' et R'' n'indiqueront pas la même heure.
Ainsi, lors du demi-tour il y a un changement brutal de l'heure des horloges (en passant de R' à R''). Cela se voit sur les transformations de Lorentz : t' dépend du temps t mais aussi de la position x (ce que l'on oublie parfois dans les raisonnements trop simples n'utilisant que la dilatation du temps) mais aussi de la vitesse. Lorsque le signe de la vitesse s'inverse, loin d'Alain (x non nul), les transformations de Lorentz montrent que t' varie brusquement.
Bien entendu, Bernard ne décide pas de changer brutalement son horloge ! Celle-ci continue à fonctionner normalement, au rythme du temps propre. De son point de vue, c'est donc l'horloge d'Alain qui effectue un brusque saut dans le futur.
Notons que si l'accélération était progressive (un demi-tour moins brutal), Bernard constaterait simplement un vieillissement rapide d'Alain.
Certaines explications invoquent l'effet dû à l'accélération. Mais c'est faux. Le phénomène ci-dessus est clairement dû au choix de la synchronisation des horloges. Comment l'accélération de Bernard pourrait-elle faire brutalement vieillir Alain ! Elle pourrait, imaginons le, "geler" le temps de Bernard. Mais nous savons que ce n'est pas ce qu'Alain constate : il ne voit pas Bernard "immobile" pendant une longue durée lors de son demi-tour.
En réalité, l'accélération n'est responsable que de deux choses. D'une part la rupture de symétrie dans la situation et d'autre part de l'invalidation de certains raisonnements utilisant, par exemple la dilatation du temps comme dans la formulation initiale du paradoxe.
Ce problème de synchronisation, bien connu en relativité restreinte, est dû au fait qu'il est impossible de comparer directement deux horloges si elles ne sont pas côte à côte. Il faut fatalement un protocole de synchronisation utilisant, par exemple, un déplacement des horloges ou l'échange de signaux. Et le résultat dépend donc de la synchronisation adoptée.
Attention, seul le résultat "en cours de voyage" est affecté, l'analyse de ce qui se passe. Le résultat final, lui, reste identique.
Il convient donc de bien distinguer les effets apparents (Doppler), les effets réels (le résultat final) et ceux dûs au choix de la synchronisation. Ce que le paradoxe des jumeaux permet d'illustrer de manière admirable.
Le choix du repère inertiel
Il nous reste à régler un problème. Nous avons plus haut choisi arbitrairement le repère d'Alain comme étant le repère inertiel.
Mais pourquoi est-ce le repère terrestre qui est inertiel et pas celui de Bernard ?
Pour être plus précis, signalons que le repère terrestre n'est pas tout à fait inertiel. Outre des difficultés liées à la présence de la gravitation, il faut, en principe, tenir compte des effets de la force centrifuge et de la force de Coriolis (dus à la rotation de la Terre). Mais on peut considérer une situation où Alain et Bernard sont dans l'espace, loin de tout et où ensuite Bernard entame son voyage (avec des accélérations)
Pourquoi c'est Alain qui est inertiel et pas Bernard puisque le point de vue peut être totalement inversé ?
Cela revient en fait à justifier l'existence des repères inertiels. En fait, l'existence de ces repères est évidente (à partir d'un repère quelconque non inertiel, avec une accélération a, en choisissant un autre repère ayant une accélération relative − a, on aura forcément un repère inertiel). Ce qui est plus difficile à justifier est le fait que ce soit tel repère particulier qui est inertiel plutôt que tel autre.
Évidemment, on trouve facilement (et donc on les justifie) les repères inertiels car il suffit d'attacher un repère au centre de masse d'un système libre de toute interaction avec l'extérieur (au moins idéalement ou par la pensée), c’est-à-dire ne subissant pas de forces extérieures. Mais cette approche est quelque peu délicate car on peut définir les forces par leur effet (ici, l'accélération) et cela conduit à une justification dangereusement tautologique.
La question en physique newtonienne ne se pose pas vraiment puisque l'on considère implicitement l'existence d'un espace absolu.
La relativité restreinte n'est guère différente à ce sujet. Elle se contente de postuler l'existence des repères inertiels et c'est tout. Mais c'est un peu bizarre car en relativité restreinte, il n'y a pas d'espace absolu. Pas de "scène de théâtre" à laquelle rattacher les repères inertiels. La relativité restreinte n'est pas à même de justifier que ce soit telle classe de repère qui est inertielle plutôt que telle autre. Pas plus que la physique newtonienne puisque la relativité galiléenne montre bien que même dans le cas newtonien on ne peut pas non plus vraiment parler de repère absolu.
Nous pouvons, bien entendu, identifier les effets physiques (nous avons parlé par exemple de la force centrifuge) pour identifier les repères non inertiels. Mais c'est une justification expérimentale, pas théorique. Nous pouvons aussi identifier les causes physiques (par exemple la présence de fusées appliquant une force à Bernard). Mais comme nous l'avons dit, si on relie les causes aux effets (une force est appliquée s'il y a un effet) et les repères aux causes (les repères non inertiels subissent une force) et comme un repère inertiel est identifié par les effets que l'on y subit, on tombe sur une justification qui se mord la queue.
C'est la relativité générale qui est venue résoudre définitivement ce dilemme. En relativité générale, la géométrie de l'espace-temps (sa métrique, par exemple) est directement reliée à la présence de matière (par l'équation d'Einstein). L'espace est courbe et en chaque point on peut trouver un espace-temps de Minkowski tangent à l'espace-temps courbe (la connexion affine) et cela permet ainsi de trouver les repères inertiels. Les corps inertiels (immobiles dans un repère inertiel) sont en "chute libre" (sans autre influence que la gravitation) et suivent les géodésiques de l'espace-temps courbe.
Explication de la relativité générale
En relativité générale, on travaille donc dans un espace-temps courbe dont la métrique est connue ou calculée à partir de la distribution de matière.
Pour connaître le temps écoulé pour un individu quelconque, il faut généraliser la méthode que nous avons vue plus haut. On dispose de la métrique décrivant la géométrie de l'espace-temps, habituellement écrite comme :
ds2 = gμνxμxν
Cette métrique donne immédiatement le temps propre et peut être intégrée le long de la trajectoire pour connaître le temps propre total écoulé. La trajectoire étant imposée ou calculée (par exemple une géodésique en utilisant l'équation des géodésiques de la relativité générale).
Ici, le paradoxe des jumeaux ne fait pas intervenir la gravitation. La métrique est simplement donnée par le tenseur de Minkowski gμν = ημν. Et on retrouve les résultats qui précèdent.
Toutefois, il est malgré tout possible de travailler avec le formalisme plus complet de la relativité générale. Ainsi, il est possible de travailler dans le repère de Bernard, ce que nous avons soigneusement évité jusqu'ici.
Le repère de Bernard étant accéléré, les géodésiques seront des courbes. En effet, dans le repère inertiel, les géodésiques (obtenues avec des corps en mouvement qui ne subissent aucune force) sont des droites. Et dans le repère accéléré ces droites deviennent des courbes.
En physique newtonienne la situation ne serait pas bien dramatique car l'espace et le temps sont indépendants. Plutôt que de travailler avec un espace courbe, on peut, par exemple, ajouter des forces fictives (force centrifuge, force de Coriolis, force d'inertie) qui reproduisent les mêmes effets de courbure des trajectoires.
Mais en relativité restreinte, l'espace et le temps sont étroitement mêlés. C'est l'espace-temps entier qui est affecté et il n'est plus si facile de se débarrasser des coordonnées curvilignes.
Par contre on peut alors utiliser la métrique plus générale ci-dessus et dans le cas, par exemple, d'un repère accéléré (accélération constante), on obtient ce que l'on appelle un modèle (en fait une métrique) de Rindler.
On peut utiliser tout l'arsenal de la relativité générale (les mathématiques tensorielles et les espaces de Riemann). On constate que dans le cas présent, malgré la présence de coordonnées curvilignes, l'espace-temps ainsi défini reste plat (sans courbure). Cela n'est pas surprenant en l'absence de gravitation pour affecter la courbure de l'espace-temps et même dans l'espace euclidien on peut utiliser des coordonnées curvilignes telles que les coordonnées sphériques. Les coordonnées curvilignes dans l'espace-temps de Minkowski sont simplement un peu plus compliquées.
Ce qui est obtenu est donc une généralisation de la relativité restreinte mais sans la gravitation. Ou une restriction de la relativité générale aux espaces-temps plats et sans l'utilisation de l'équation d'Einstein.
Ce formalisme est plus compliqué que celui de la relativité restreinte mais a l'avantage d'autoriser très facilement le passage à des situations où la gravité est présente.
Voyons dans notre cas ce que l'on obtient. Ici le repère de Bernard est en fait non accéléré pendant presque tout son voyage, et ses coordonnées devraient être essentiellement rectilignes. Par contre, lors du demi-tour il subit une accélération instantanée et brutale. On doit donc observer une discontinuité.
Une situation plus réaliste, avec un demi-tour plus progressif, pourrait aussi être utilisée.
Comment se présentent les trajectoires dans son diagramme espace-temps ? Comme Bernard est immobile dans son repère sa trajectoire sera verticale. Mais les lignes de simultanéité ne peuvent être horizontales, comme le montre le dernier diagramme. Elles seront donc inclinées avec une discontinuité au niveau du demi-tour. On obtiendra un diagramme semblable à celui-ci :
La trajectoire d'Alain (dans le tableau appelé Alex) subit une discontinuité associée à un brusque vieillissement (dû au choix de la synchronisation), ce qui est tout à fait normal.
Autres situations
Il est possible d'étendre ce paradoxe à toutes sortes de situations. Par exemple on peut envisager le cas où les jumeaux entament chacun un voyage mais dans des directions opposées (jumeaux symétriques). Ou des situations avec des triplés ou encore bien d'autres complications.
Tous ces cas se résolvent aisément par les méthodes que nous avons vues en choisissant le repère inertiel approprié.
Une situation fréquemment invoquée est celui où Bernard ne fait pas un aller-retour mais parcourt une trajectoire circulaire (par exemple autour de la Terre). On pourrait croire que dans ce cas il n'y a pas d'accélération puisque la vitesse (en grandeur) reste constante. Mais la vitesse varie en direction et l'accélération est bien présente, il s'agit ici d'une accélération centripète (cause de sa rotation, par exemple la gravitation dans le cas d'un satellite). Ce cas se résout de la même manière en choisissant le repère inertiel approprié (par exemple celui d'Alain resté au sol). Dans le cas d'une vitesse constante en grandeur la solution est tout aussi immédiate que dans le cas du paradoxe des jumeaux traditionnel.
Evoquons brièvement une situation assez particulière. Cette fois, Bernard et Alain effectuent tous les deux une trajectoire circulaire (dans le repère inertiel) mais dans des sens opposés.
Du point de vue du repère inertiel la situation est semblable à celle du cas précédent ou du paradoxe des jumeaux. Alain et Bernard subissent tous les deux l'effet de la dilatation du temps et lorsqu'ils se rencontrent, ils ont toujours le même âge.
La dilatation du temps d'Alain peut être compliquée du point de vue de Bernard. Il faudrait faire le calcul complet dans des repères en rotation pour le savoir. Mais cette dilatation doit exister au moins à certains moments car leur vitesse relative est non nulle. Et cette dilatation (donnée par 1 / γ) est toujours inférieure à un.
Selon que l'on considère le point de vue de Bernard et Alain, on retombe sur le paradoxe initial. Et cette fois les accélérations ne peuvent être invoquées puisqu'il y a totale symétrie, comme le montre la figure ci-dessus.
Ce qui intervient ici est un effet appelé effet Sagnac.
Supposons qu'un observateur animé d'un mouvement de rotation (comme Bernard ou Alain ici) envoie le long de la circonférence deux signaux à même vitesse (par rapport à lui, localement dans son repère, dans le cas où ces signaux seraient moins rapides que la vitesse de la lumière dans le vide, comme avec des signaux dans une fibre optique ou avec des particules) mais dans des sens opposés. Il constate alors que les deux signaux lui reviennent avec un décalage temporel. De plus, ce décalage est "universel" en ce sens qu'il dépend de la vitesse de rotation de l'observateur mais pas de la vitesse des signaux utilisés.
Lorsque l'on étudie la géométrie de l'espace-temps dans un repère en rotation, on constate que pour une trajectoire circulaire, il y a un Time Gap égal à celui de l'effet Sagnac et tout à fait analogue à celui que nous avons vu plus haut avec le point de vue de Bernard. Dans l'espace-temps d'un repère en rotation, si l'on tente de feuilleter l'espace-temps avec des surfaces spatiales, on obtient une curieuse structure spiralée qui reflète les difficultés de synchronisation des horloges dans un repère en rotation (les lignes de simultanéités ne se referment pas sur elles-mêmes). Dans le cas d'un espace-temps euclidien et avec des coordonnées curvilignes dues à l'accélération, ce genre d'effet n'est pas observé. Nous constatons ici une conséquence typique de l'intrication de l'espace et du temps en relativité restreinte.
Ce Time Gap, compense la dilatation du temps et Alain et Bernard auront le même âge lors de leurs retrouvailles.
Donc, lorsque Bernard est en rotation autour d'un corps massif (par exemple s'il est dans un satellite en orbite autour de la Terre), trois approches sont possibles :
- On peut considérer le point de vue de la relativité générale. On calcule la métrique autour d'un corps massif (par exemple une métrique de Schwarzschild) et on calcule les temps écoulés par la méthode généralisée. Dans des situations compliquées ces calculs peuvent être ardus.
- On peut considérer le point de vue de la relativité restreinte. Dans ce cadre, le repère au sol est inertiel (ou presque compte tenu de la force centrifuge et de Coriolis). Contrairement à la relativité générale où les repères inertiels sont ceux en chute libre. En effet, en relativité restreinte la gravité n'est pas expliquée par la géométrie de l'espace-temps mais est une force comme les autres. Un corps immobile au sol voit cette force compensée par la force de réaction du support (le sol) qui l'empêche de s'enfoncer. Et il est donc considéré comme inertiel (la résultante des forces est nulle). On applique alors les méthodes que nous avons vues pour des trajectoires quelconques dans un espace-temps de Minkowski.
- On peut enfin utiliser une approche mixte. En effet, les résultats obtenus par la relativité restreinte ne sont pas tout à fait corrects. Il y a deux raisons à cela. Premièrement, la gravité ne peut pas être correctement décrite en relativité restreinte, c'est sous l'impulsion de ce constat qu'Einstein s'est lancé dans l'élaboration de la relativité générale. Deuxièmement, certains effets ne sont pas prédits en relativité restreinte comme le décalage vers le rouge gravitationnel (en fait, ce sont ces effets qui expliquent que la relativité restreinte n'est pas appropriée pour décrire la gravité). Si l'on place une horloge en altitude, on constate que son rythme est un peu plus rapide que celui d'une horloge restée au sol. L'effet est déjà mesurable sur des hauteurs modestes (un immeuble). L'approche mixte consiste donc à utiliser la relativité restreinte et à apporter des corrections gravitationnelles comme le décalage vers le rouge gravitationnel. C'est cette méthode qui est utilisée pour le GPS qui nécessite une synchronisation extrêmement précise des horloges. En fait, pour être exact, ces corrections sont calculées au sol, à l'avance, et introduites artificiellement dans les horloges des satellites sous forme d'une modification du rythme des horloges. Ensuite, comme il y a toujours des imprécisions et des perturbations (les trajectoires des satellites ne sont pas des circonférences parfaites), des corrections sont effectuées régulièrement (et cette fois par calcul en ligne) par synchronisation entre satellites et avec les stations au sol.
Restriction la plus fréquente du paradoxe
Certaines personnes peuvent aussi penser dans un premier temps que le fait que le temps n'aille pas à la même vitesse pour tout le monde est lui-même paradoxal ; en fait, cette question était déjà patente dès 1905 (et même avant avec les transformations de Lorentz), et il n'était nul besoin d'attendre 1911 pour la mettre en évidence. Le fait que le temps puisse ne pas s'écouler à la même vitesse subjectivement est bien connu dans la vie courante, et le fait que des différences objectives puissent exister aussi n'ont probablement pas de quoi surprendre outre mesure une fois que l'on se débarrasse du postulat du temps absolu (qui n'a pas de base objective). L'impossibilité de comparer directement des horloges distantes rend même tout à fait plausible de telles circonstances.
Le paradoxe est souvent présenté de cette seconde manière - ou même, en mettant les choses au mieux, dans des termes qui rendent cette seconde interprétation possible. Il serait donc opportun de distinguer par le vocabulaire :
- Le paradoxe lui-même, tel qu'il a été posé par Langevin, paradoxe levé dès qu'on note la dissymétrie entre les jumeaux, dissymétrie produite par les accélérations.
- Le phénomène d'un vieillissement différencié entre les deux jumeaux. Dans l'article Calculs relativistes, ce dernier phénomène a été baptisé le voyage dans le futur des autres.
Apport épistémologique
Les contresens eux-mêmes sont instructifs quand on les aborde dans le cadre de l'épistémologie ou des sciences cognitives. Ceux relatifs au paradoxe de Langevin nous apprennent ainsi à éviter plusieurs erreurs :
- utiliser des résultats théoriques (dilatation du temps, transformations de Lorentz) dans des situations où ils sont invalides (repères accélérés).
- attribuer à la relativité de simples effets apparents (comme dans le cas de l'effet Doppler), qui auraient aussi bien lieu en utilisant d'autres signaux comme des signaux sonores, oubliant ainsi le caractère symétrique des effets relativistes. En effet, la synchronisation d'horloges distantes par envoi de signaux sonores ne permet pas, à elle seule, de mimer la symétrie des effets relativistes. Pour que l'analogie formelle onde sonore/onde lumineuse respecte la symétrie des effets relativistes, il faudrait considérer des "objets" formés d'ondes sonores stationnaires subissant la contraction de Lorentz (quand ces ondes sont stationnaires dans un référentiel en mouvement à vitesse constante par rapport au milieu où ces ondes sonores se propagent).
- attribuer à la synchronisation relativiste, le caractère de procédure arbitraire pour synchroniser la position initiale des aiguilles d'horloges distantes, alors que ce choix exprime au contraire le caractère objectivement privilégié des systèmes de coordonnées inertiels (les systèmes de coordonnées orthonormés vis à vis de la métrique de Minkowski), seuls systèmes de coordonnées permettant une expression covariante des lois de la physique lors d'un changement de référentiel inertiel (exprimant ainsi naturellement l'invariance des lois de la physique vis à vis des actions du groupe de Poincaré).
- croire que la relativité générale est absolument indispensable en présence d'accélérations de particules ponctuelles et en l'absence de gravitation.
- attribuer aux accélérations un effet physique direct sur l'écoulement du temps alors qu'elles ne sont responsables que d'une rupture de symétrie, l'effet réel résultant plus de considérations géométriques (la relativité du mouvement contenue dans l'invariance des lois de la physique vis à vis des actions du groupe de Poincaré, se limite aux mouvements de translation à vitesse constante) et du choix du repère inertiel.
- qualifier de paradoxal un effet qui n'est que surprenant.
Autres paradoxes en physique
- Petites expériences de pensée
- Le paradoxe du train
- Le démon de Maxwell
- Voir la liste de paradoxes

















































