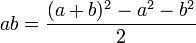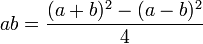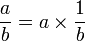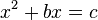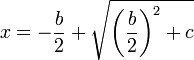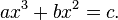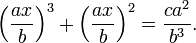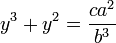Mathématiques babyloniennes - Définition

Introduction

Photographie de la tablette YBC 7289 annotée. Les nombres écrits dans le système babylonien donnent la racine carrée de 2 avec quatre chiffres sexagésimaux significatifs, soit près de six chiffres décimaux :
1 + 24/60 + 51/60² + 10/60³ = 1,41421296... (crédit : Bill Casselman).

Les mathématiques babyloniennes sont les mathématiques pratiquées par les peuples de l'ancienne Mésopotamie (dans l’Irak actuel), depuis l'époque des Sumériens jusqu'à la chute de Babylone en 539 av. J. Chr.. Alors que l'on ne dispose que de très rares sources sur les mathématiques en Égypte antique, notre connaissance des mathématiques babyloniennes s'appuie sur environ 400 tablettes d'argile mises au jour depuis les années 1850. Écrites en cunéiforme, ces tablettes furent travaillées sur de l'argile encore humide, puis cuites dans un four ou séchées au soleil.La plupart des tablettes qui nous sont parvenues datent de 1800 à 1600 av. J. Chr., et traitent de fractions, d’équations algébriques (équations du second degré et du troisième degré), de calculs d'hypoténuse et de triplets pythagoriciens voire, peut-être, de certaines lignes trigonométriques (cf. notamment la tablette Plimpton 322). La tablette YBC 7289 fournit une approximation de précise à six décimales près.

Numération babylonienne

Le système de numération en usage chez les Babyloniens était de type sexagésimal (« base 60 »). C'est d'ailleurs des Babyloniens que nous avons hérité l'usage de diviser les heures en soixante minutes, et chaque minute en 60 secondes, et aussi de diviser la circonférence d'un cercle en 360 (60×6) degrés. Le développement des mathématiques chez les Babyloniens tient à deux choses ; tout d'abord, au fait que le nombre 60 est un nombre hautement composé, dont les nombreux diviseurs : 2, 3, 4, 5, 6, 10, 12, 15, 20, et 30, facilitent les calculs de fractions ; ensuite, à ceci que, contrairement aux Égyptiens et aux Romains, les Babyloniens (comme plus tard les Indiens) disposaient d'un authentique système à numération de position, où les chiffres les plus à gauche représentent les plus grandes valeurs (exactement comme dans notre système décimal : 734 = 7×100 + 3×10 + 4×1).

Deux signes étaient utilisés : pour désigner l'unité et pour la dizaine. On écrivait plusieurs pour les nombres jusqu'à neuf et plusieurs pour les dizaines, jusqu'à cinq dizaines. Il est à noter que les Babyloniens écrivaient de la même manière les nombres égaux à un facteur 60 près.

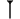
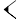
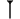
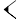
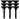
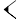
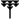
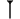
Les mathématiques dans l'ancienne Babylonie (2000-1600 av. J. Chr.)

C’est à la période paléo-babylonienne que se rattachent la plupart des tablettes à contenu mathématique, ce qui explique d'ailleurs pourquoi on a coutume d'appeler les mathématiques de Mésopotamie « mathématiques babyloniennes ». Certaines tablettes comportent des listes ou des tableaux de nombres, d'autres des énoncés de problèmes et leur solution.

Arithmétique

Multiplication

Les Babyloniens utilisaient massivement les tables numériques pour le calcul et la résolution de problèmes d'arithmétique. Par exemple, deux tablettes trouvées à Senkerah sur l’Euphrate en 1854, datées de 2000 av. J. Chr., sont des listes des carrés d’entiers jusqu'à 59 et de cubes jusqu’à 32. Les Babyloniens s'en servaient pour effectuer les multiplications, avec les identités :

Division

Les Babyloniens ne posaient pas de division. Pour ce genre de calcul, ils se ramenaient au produit :

et recouraient à une table d’inverses. L’inverse des nombres n'ayant comme facteurs premiers que 2, 3 ou 5 (appelés « nombres 5-lisses » ou « nombres réguliers ») s'écrit avec un nombre fini de chiffres en écriture sexagésimale : or on a retrouvé un grand nombre de tables donnant les inverses de tels nombres entiers.

Il faut se souvenir que pouvait désigner aussi bien ce que nous noterions 1 que 60 ou 60². Deux nombres étaient inverses l'un de l'autre lorsque leur produit était une puissance de soixante. Ainsi, l'« inverse » de (2) était (30) car 2×30 = 60. La table d'inverses classique était (en base 60 avec deux points ':' pour séparateur des chiffres) :

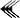
         2    30           16    3:45          45    1:20         3    20           18    3:20          48    1:15         4    15           20    3             50    1:12         5    12           24    2:30          54    1: 6:40         6    10           25    2:24        1       1         8     7:30        27    2:13:20     1: 4      56:15         9     6:40        30    2           1:12      50        10     6           32    1:52:30     1:15      48        12     5           36    1:40        1:20      45        15     4           40    1:30        1:21      44:26:40      

où 6:40, qui désigne 6×60+40 est mis en relation avec 9 car 9×(6×60+40) = 3600 = 60². Donc 9 est l'inverse de 6×60+40 au sens babylonien du terme

Au contraire, des inverses comme 1/7, 1/11, 1/13, etc. n'ont pas de représentation finie en écriture sexagésimale. Pour calculer 1/13 ou pour diviser un nombre par 13, les Babyloniens recouraient à une approximation de la forme

.

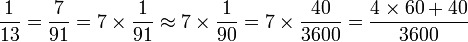
Algèbre

Outre les calculs d'arithmétique, les mathématiciens Babyloniens imaginèrent aussi des algorithmes pour résoudre certaines équations algébriques. Là encore, ils recouraient à des tables numériques.

Pour résoudre une équation du second degré, les Babyloniens se ramenaient fondamentalement à la forme canonique

où les coefficients b et c ne sont pas nécessairement des entiers, mais où c est toujours positif. Ils savaient que la solution positive (la seule qui avait un sens pour eux) à une équation de cette forme s'obtient par la formule

et se servaient de tables de carrés pour trouver les racines carrées intervenant dans cette formule. Parmi les énoncés concrets pouvant se ramener à ce type de calcul, il y avait celui demandant de trouver les dimensions d’un rectangle connaissant sa surface et l’excédent de sa longueur sur sa largeur.

Certaines équations du troisième degré pouvaient être résolues à l'aide de tables de n³+n². Par exemple, soit l’équation

Multipliant l’équation par a² et la divisant par b³, on obtient

Substituant y = ax/b, cela donne

équation que l'on peut résoudre en consultant une table de n³+n² pour trouver la valeur la plus proche du second membre. Les Babyloniens exécutaient ces calculs sans véritablement poser les opérations algébriques, ce qui témoigne d'une remarquable capacité de concentration. Cependant, ils n'avaient pas d'algorithme général pour résoudre une équation du troisième degré quelconque.

Géométrie

Il est possible que les Babyloniens aient disposé de règles générales pour calculer la surface et le volume de certaines figures géométriques. Ils calculaient la circonférence du cercle en prenant trois fois le diamètre, et la surface du cercle en prenant un douzième du carré de la circonférence, ce qui revient à prendre pour π la valeur que l'on trouve aussi dans la Bible, à savoir 3. Le volume d'un cylindre était calculé en formant le produit de sa base par sa hauteur ; par contre, le calcul du volume du cône tronqué ou de la pyramide à base carrée était incorrect : les Babyloniens formaient le produit de la hauteur par la demi-somme (c'est-à-dire la moyenne) des bases. Ils connaissaient le théorème de Pythagore en tant que formule, sans que l'on ait trace d'une démonstration en tant que telle. On a découvert récemment une tablette où l'on prend pour π la valeur 3 + 1/8. Les Babyloniens mesuraient les distances en utilisant le mille babylonien, représentant environ 10 km. Cette unité de mesure avait un équivalent horaire, ce qui permettait de convertir les positions du Soleil dans le ciel en heure du jour.

Trigonométrie

Si les anciens Babyloniens connaissaient depuis des siècles l’égalité des rapports entre les côtés de triangles semblables, le concept d’angle leur était étranger : aussi se ramenaient-ils à des considérations sur les longueurs des côtés.

Les astronomes babyloniens tenaient une chronique précise des levers et couchers des étoiles, du mouvement des planètes et des éclipses solaires et lunaires, autant de précisions qui supposent une familiarité avec les distances angulaires mesurées sur la sphère céleste.

Les Babyloniens paraissent avoir été les premiers à utiliser les lignes trigonométriques, comme en témoigne une table de nombres portés sur une tablette en écriture cunéiforme, la Tablette Plimpton 322 (circa 1900 BC), qu'on peut interpréter comme une table trigonométrique de sécantes.

Avec la redécouverte de la civilisation babylonienne, il est apparu que les mathématiciens et les astronomes grecs de la période classique et hellénistique, en particulier Hipparque de Nicée, ont beaucoup emprunté aux Chaldéens.

Franz Xaver Kugler, par exemple, a montré la chose suivante : Ptolémée, dans l’Almageste, indique qu’Hipparque a corrigé la durée des phases de la Lune transmises par « des astronomes encore plus anciens » en rapportant les observations des éclipse faite auparavant par « les Chaldéens » aux siennes. Or, Kugler a montré que les périodes que Ptolémée attribue à Hipparque étaient déjà utilisées dans des éphémérides babyloniens, à savoir le recueil nommé « Système B » (parfois attribué à Kidinnu). Apparemment, Hipparque s'est borné à confirmer par ses observations l'exactitude des valeurs de périodes qu'il avait lues dans les écrits des Chaldéens.

Il est évident qu’Hipparque (et Ptolémée à sa suite) disposait d'une liste complète des observations d’éclipses sur plusieurs siècles. Celles-ci avaient très probablement été compilées à partir des « tablettes-journaux », tablettes d'argile contenant toutes les observations significatives effectuées au jour le jour par les Chaldéens. Les exemplaires préservés datent de 652 av. J. Chr. à 130 de notre ère, mais les événements célestes qui y sont consignés remontent très probablement au règne du roi Nabonassar : car Ptolémée fait commencer sa chronologie au premier jour du calendrier égyptien, la première année du règne de Nabonassar, c’est-à-dire le 26 février 747 av. J. Chr.

Il n'a pas dû être facile d'exploiter toute cette masse d'observations, et il n'est pas douteux que les Chaldéens eux-mêmes se servaient de tables abrégées contenant, par exemple, uniquement les éclipses observées (on a trouvé quelques tablettes portant une liste de toutes les éclipses sur une période correspondant à un « saros »). Ces tables leur permettaient déjà de constater le retour périodique de certains phénomènes. Parmi les périodes utilisées dans le recueil du « Système B » (cf. Almageste IV.2), on trouve :

• 223 mois (synodiques) = 239 passages au périgée (mois anomalistique) = 242 passages sur la ligne des nœuds (mois draconitique). Cette période est appelée période de saros : elle est très pratique pour calculer les périodes d'occurrence des éclipses.
• 251 mois (synodiques)= 269 passages au périgée
• 5458 mois (synodiques)= 5923 passages à la ligne des nœuds
• 1 mois synodique = 29;31:50:08:20 jours (dans le système sexagésimal; 29.53059413… jours en numération décimales = 29 jours 12 heures 44 min 3⅓ s)

Les Babyloniens exprimaient toutes les périodes en mois synodiques, probablement parce qu'ils utilisaient un calendrier luni-solaire. Le choix des intervalles entre les phénomènes célestes périodiques survenant en l'espace d'une année donnait différentes valeurs pour la longueur d'une année.

De même, on connaissait plusieurs relations entre les périodes des planètes. Les relations que Ptolémée attribue à Hipparque avaient déjà servi pour des prédictions retrouvées sur des tablettes babyloniennes.

Toutes ces connaissances passèrent aux Grecs, sans doute peu après la conquête d’Alexandre le Grand (-331). Selon le philosophe Simplicius (début du VI^e siècle), Alexandre avait ordonné la traduction des éphémérides astronomiques chaldéens, et en avait confié la supervision à son biographe Callisthène d’Olynthos, qui les envoya à son oncle Aristote. Si Simplicius ne nous offre qu'un témoignage tardif, son récit n'en est pas moins fiable, car il passa quelques temps en exil à la cour des Sassanides, et a pu avoir accès à des sources documentaires ayant disparu en Occident. Ainsi il est frappant qu'il emploie le titre tèresis (en grec: « veille »), étrange pour un livre d'histoire, mais qui constitue une traduction précise du babylonien massartu qui signifie « monter la garde » mais également « observer ». Quoi qu'il en soit, c’est vers cette époque que Calippe de Cyzique, un élève d’Aristote, proposa l’emploi d'un cycle de 76 ans, qui améliore le cycle de Méton, d'une durée de 19 ans. Il faisait démarrer la première année de son premier cycle au solstice d’été (28 juin) de l'an 330 av. J. Chr. (date julienne prolepse), mais par la suite il semble qu'il ait compté les mois lunaire à partir du mois suivant la victoire d’Alexandre à la bataille de Gaugamèles, à l'automne 331 av. J. Chr. Ainsi, Calippe a pu obtenir ses données de sources babyloniennes, et il est donc possible que son calendrier soit antérieur à celui de Kidinnu. On sait par ailleurs que le prêtre babylonien connu sous le nom de Bérose écrivit vers 281 av. J. Chr. une histoire (à caractère plutôt mythologique) en grec de la Babylonie, les Babyloniaca, dédiées au nouveau monarque Antiochos Ier ; et l’on dit qu’il fonda par la suite une école d’astrologie sur l’île grecque de Cos. Parmi les autres auteurs qui ont pu transmettre aux Grecs les connaissances babyloniennes en astronomie-astrologie, citons Sudines qui vivait à la cour du roi Attale Ier Sôter à la fin du III^e siècle av. J.-C..

Quoi qu’il en soit, la traduction de ces annales astronomiques exigeait une connaissance profonde de l’écriture cunéiforme, de la langue et des méthodes, de sorte qu’il est vraisemblable qu'on a confié cette tâche à un Chaldéen dont le nom ne nous est pas parvenu. Les Babyloniens, en effet, dataient leurs observations dans leur calendrier luni-solaire, dans lequel la durée des mois et des années n'est pas fixe (29 ou 30 jours pour les mois ; 12 ou 13 mois pour les années). Qui plus est, à cette époque il n'utilisaient pas encore de calendrier régulier (fondé par exemple sur un cycle, comme le cycle de Méton), mais faisaient démarrer un mois à chaque nouvelle Lune. Cette pratique rendait fastidieux le calcul du temps séparant deux événements.

La contribution d’Hipparque a dû consister à convertir ces données en dates du calendrier égyptien, qui est fondé sur une année d'une durée fixe de 365 jours (soit 12 mois de 30 jours et 5 jours supplémentaires) : ainsi le calcul des intervalles de temps est beaucoup plus simple. Ptolémée datait toutes ses observations dans ce calendrier. Il écrit d’ailleurs que « Tout ce qu'il (=Hipparque) a fait, c'est une compilation des observations des planètes ordonnée de façon plus commode. » Pline l'Ancien, traitant de la prédiction des éclipses écrit : « Après eux(=Thalès) les positions des deux astres (=le Soleil et la Lune) pour les 600 années à venir furent annoncées par Hipparque, … » Cela doit vouloir dire qu'Hipparque a prédit les éclipses pour une période de 600 ans, mais étant donné l'énorme quantité de calculs que cela représente, c'est très peu probable. Plus vraisemblablement, Hipparque aura compilé une liste de toutes les éclipses survenues entre le temps de Nabonasser et le sien.

Voici d'autres traces de pratiques babyloniennes dans l’œuvre d’Hipparque :

• Hipparque est le premier auteur grec à avoir divisé le cercle en 360 degrés de 60 minutes.
• il est le premier à avoir utilisé systématiquement la numération sexagesimale .
• il a utilisé le pechus (« coudée »), unité d'angle de 2° ou 2½° d'ouverture.
• il a utilisé la courte période de 248 jours = 9 mois anomalistiques.