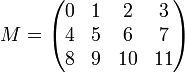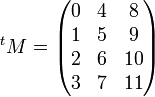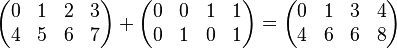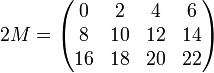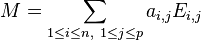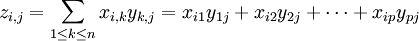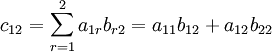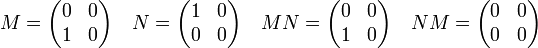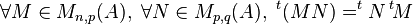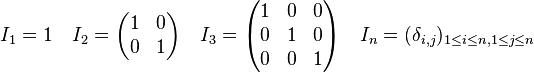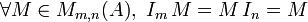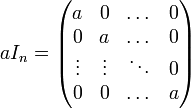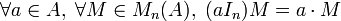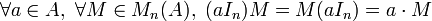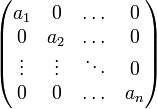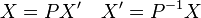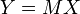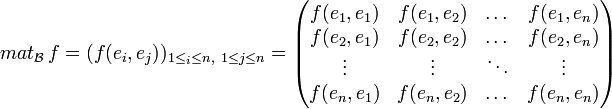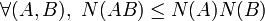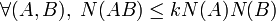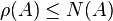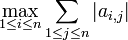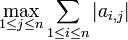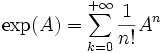Matrice (mathématiques) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

En mathématiques, les matrices servent à interpréter en termes calculatoires et donc opérationnels les résultats théoriques de l'algèbre linéaire et même de l'algèbre bilinéaire. Toutes les disciplines étudiant des phénomènes linéaires utilisent les matrices. Quant aux phénomènes non linéaires, on en donne souvent des approximations linéaires comme c'est le cas en optique géométrique avec les approximations de Gauss.

Définitions

Soient $A$ un ensemble et (m,n) un couple d'entiers positifs.

On appelle matrice à coefficients dans A, corps commutatif quelconque, de dimension (ou taille) (m,n) -ie à m lignes et n colonnes-, une famille (a_i,j)d'éléments de A indexée par le produit cartésien des ensembles de nombres entiers $[1, m]$ et $[1, n]$ .

La matrice M pourra être notée par

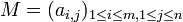
ou plus simplement (a_i,j)_i,j, voire (a_i,j) si le contexte s'y prête.

On représente généralement une matrice sous la forme d'un tableau rectangulaire. Par exemple, est représentée ci-dessous une matrice M, à coefficients entiers, et de dimension (3,4) :

M=\begin{pmatrix} 0 &1 & 2 & 3\\ 4 & 5 & 6 & 7\\ 8 & 9 & 10 & 11\\ \end{pmatrix}

Dans cette représentation, le premier coefficient de la dimension est le nombre de lignes, et le deuxième, le nombre de colonnes du tableau. Une matrice pour laquelle le nombre m de lignes est égal au nombre n de colonnes sera dite matrice carrée de taille n. Une matrice ne comportant qu'une seule ligne et n colonnes est appellée matrice ligne de taille n. Une matrice ne comportant m lignes et une seule colonne est appellée matrice colonne de taille m.

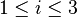
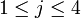
Pour repérer un coefficient d'une matrice, on indique son indice de ligne puis son indice de colonne, les lignes se comptant du haut vers le bas et les colonnes de la gauche vers la droite. Par exemple, on notera a_i,j, les coefficients de la matrice M, pour $1\le i\le 3$ désignant le numéro de la ligne sur laquelle figure le coefficient envisagé, et $1\le j\le 4$ désignant son numéro de colonne ; ainsi a_2,4=7.

La disposition générale des coefficients d'une matrice M de taille (m,n) est donc la suivante

M=\begin{bmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n}\\ a_{2,1} & a_{2,2} & \cdots & a_{2,n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{m,1} & a_{m,2} & \cdots & a_{m,n}\\ \end{bmatrix}

Pour effectuer certaines opérations, il peut être utile de travailler sur le système des lignes ou des colonnes d'une matrice. On pourra alors l'écrire sous une des formes suivantes

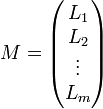
M=\begin{pmatrix} L_1\\L_2\\\vdots \\ L_m\\\end{pmatrix}

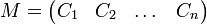
L'ensemble des matrices à coefficients dans A possédant m lignes et n colonnes est noté $M m, n (A)$ . Lorsque m=n on note plus simplement $M n (A)$ .

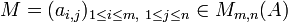
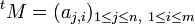
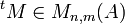
Soit $M= (a_{i,j})_{1\le i\le m,\ 1\le j\le n} \in M_{m,n}(A)$ , on appelle transposée de A la matrice $^tM=(a_{j,i})_{1\le j\le n,\ 1\le i\le m}$ . Remarquons que $^tM\in M_{n,m}(A)$ .

Par exemple, avec la matrice M des exemples précédents, on a

^tM=\begin{pmatrix} 0 & 4 & 8\\ 1 & 5 & 9\\ 2 & 6 & 10\\ 3 & 7 & 11\\ \end{pmatrix}

L'opération de transposition est involutive, c'est-à-dire que $^t{}(^t\!M)=M$ .

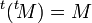
Espaces de matrices

On suppose maintenant que A est muni d'une structure d'anneau unitaire ; les éléments de A seront appelés scalaires, par opposition aux matrices dont nous allons voir qu'elles peuvent être considérées comme des vecteurs.

Addition et multiplication par un scalaire

On définit sur $M m, n (A)$ une loi de composition interne provenant de l'addition des scalaires :

(a i, j) + (b i, j) = (c i, j)

où

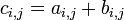
On ne peut additionner que deux matrices de même taille.

Exemple :

Pour chaque valeur du couple (m,n), l'espace $M m, n (A)$ devient alors un groupe abélien, d'élément neutre la matrice nulle, celle dont tous les coefficients valent 0.

On définit aussi une opération à gauche de A sur chaque espace $M m, n (A)$ en associant à chaque matrice $(a i, j)$ à coefficients dans A et chaque scalaire $λ$ dans A, la matrice $λ(a i, j) = (λ a i, j)$ obtenue en effectuant la multiplication, dans A, de tous les coefficients de la matrice initiale par $λ$ : c'est la multiplication par un scalaire.

En reprenant toujours la matrice M du premier exemple :

2M=\begin{pmatrix} 0 &2 & 4 & 6\\ 8 & 10 & 12 & 14\\ 16 & 18 & 20 & 22\\ \end{pmatrix}

Les espaces $M m, n (A)$ ainsi obtenus ont donc une structure de A-module à gauche, et plus particulièrement de A-espace vectoriel, si A est un corps commutatif.

Base canonique de l'espace des matrices

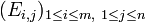
Alors $M m, n (A)$ est un $A$ -module libre de dimension $m n$ , muni d'une base canonique $(E_{i,j})_{1\le i\le m,\ 1\le j\le n}$ . La matrice $E i, j$ est celle dont tous les coefficients sont nuls sauf celui d'indice $(i, j)$ , qui vaut 1.

Pour toute matrice M, les coordonnées dans la base canonique sont les coefficients

Exemple :

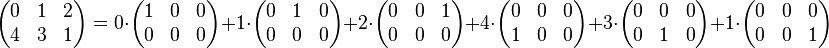
$\begin{pmatrix} 0 &1 & 2 \\ 4 & 3 & 1 \\ \end{pmatrix} = 0\cdot \begin{pmatrix} 1 &0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix} + 1\cdot \begin{pmatrix} 0 &1 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix} + 2\cdot \begin{pmatrix} 0 &0 & 1 \\ 0 & 0 & 0 \\ \end{pmatrix} + 4\cdot \begin{pmatrix} 0 &0 & 0 \\ 1 & 0 & 0 \\ \end{pmatrix} + 3\cdot \begin{pmatrix} 0 &0 & 0 \\ 0 & 1 & 0 \\ \end{pmatrix} + 1\cdot \begin{pmatrix} 0 &0 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$

Produit matriciel

On commence par définir le produit d'une matrice ligne par une matrice colonne. Soit n un nombre entier, L une matrice ligne, x_i ses coefficients, C une matrice colonne, y_i ses coefficients. On les suppose toutes deux de taille n. On définit alors le produit, considéré comme un scalaire ou une matrice de dimension (1,1) :

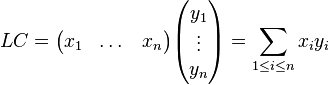
LC = \begin{pmatrix}x_1&\dots&x_n\end{pmatrix}\begin{pmatrix}y_1\\\vdots\\ y_n\end{pmatrix}=\sum_{1\le i\le n} x_iy_i

On remarque la condition de compatibilité sur les tailles des matrices (égalité du nombre de colonnes de la première avec le nombre de lignes de la deuxième). On définit maintenant plus généralement un produit entre deux matrices, la première, (x_i,j) dans $M m, n (A)$ , la deuxième, (y_i,j) dans $M n, p (A)$ , toujours avec une condition de compatibilité sur les tailles (et l'ordre des facteurs de la multiplication ne peut en général pas être changé). Le résultat obtenu est une matrice de $M m, p (A)$ , dont les coefficients (z_i,j) sont obtenus par :

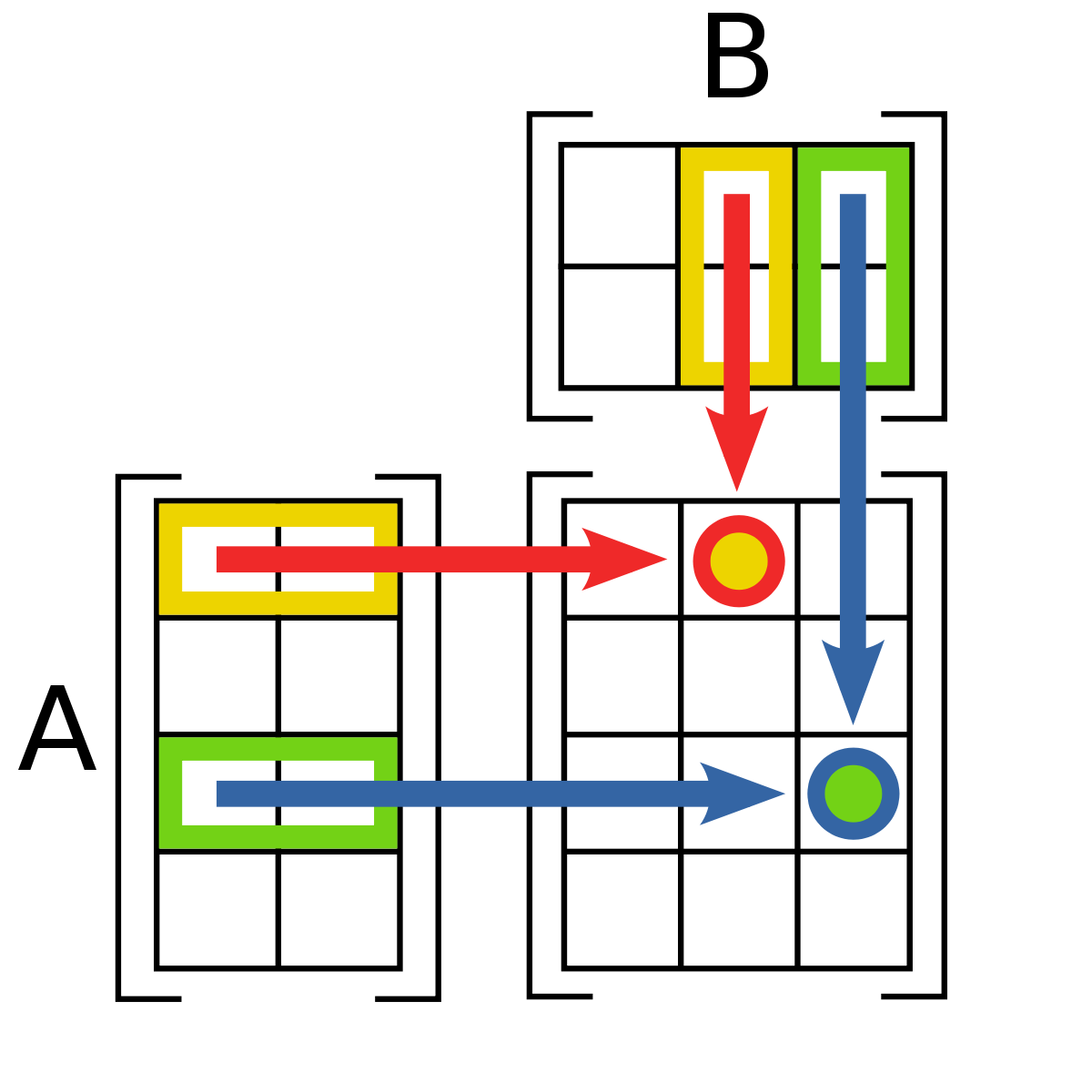
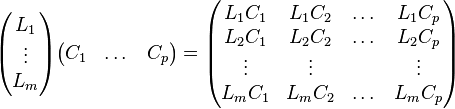
A la lumière de l'exemple de la multiplication d'une matrice ligne par une matrice colonne, on peut reformuler cette définition en disant que ce coefficient est égal au produit de la ligne i de la première matrice par la colonne j de la deuxième, ce qui s'écrit de la manière suivante, si les L_i sont les lignes de la première matrice, et les C_j les colonnes de la deuxième, le produit est : $\begin{pmatrix}L_1\\\vdots\\ L_m\end{pmatrix}\begin{pmatrix}C_1&\dots&C_p\end{pmatrix}=\begin{pmatrix} L_1C_1 & L_1C_2 & \dots & L_1C_p\\L_2C_1 & L_2C_2 & \dots & L_2C_p\\ \vdots & \vdots & & \vdots\\ L_mC_1 & L_mC_2 & \dots & L_mC_p\\\end{pmatrix}$ .

Pour calculer en pratique un produit, il est nécessaire de visualiser l'opération. On considère le coefficient $c 12$ de la matrice produit MN si M est une matrice de type (4, 2), et N est une matrice de type (2, 3).

Le produit matriciel est associatif, distributif à droite et à gauche par rapport à l'addition matricielle. En revanche, même si les dimensions permettent de donner un sens à la question, même si l'anneau des scalaires est commutatif, un produit de matrices ne commute en général pas : MN n'est pas égal à NM, par exemple :

Ce contre-exemple prouve même que les matrices MNet NM ne sont pas toujours semblables.

Lorsque l'anneau des scalaires est commutatif, la transposition et le produit matriciel vérifient la propriété :

Matrice identité et inverse d'une matrice

Pour chaque nombre entier n, on note I_n la matrice carrée de taille n dont les coefficients diagonaux sont égaux à 1 et dont les autres coefficients sont nuls ; elle est appelée matrice identité de taille n.

I_1=1\quad I_2= \begin{pmatrix} 1 & 0\\ 0 & 1\end{pmatrix} \quad I_3=\begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0 \\0 & 0 & 1 \end{pmatrix} \quad I_n=(\delta_{i,j})_{1\le i\le n,1\le j\le n}

où $δ i, j$ désigne le symbole de Kronecker.

Sous réserve de compatibilité des tailles, les matrices I_n sont neutre à droite et à gauche pour la multiplication.

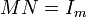
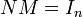
Soit M une matrice de dimension (m,n). On dit que M est inversible à droite (respectivement à gauche) si et seulement s'il existe une matrice N de taille (n,m) telle que $\displaystyle MN = I_m$ (respectivement $\displaystyle NM = I_n$ ). Pour une matrice carrée, à coefficients dans un anneau commutatif, être inversible à droite et à gauche sont deux propriétés équivalentes. Une matrice les vérifiant sera dite inversible, sans plus de précision. Le déterminant est une fonction importante sur les matrices carrées, qui permet notamment de tester leur inversibilité. 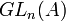Le sous-ensemble de $M n (A)$ constitué des matrices inversibles possède une structure de groupe pour le produit matriciel, est appelé groupe linéaire et noté $\displaystyle GL_n(A)$ .

Algèbre des matrices carrées

Lorsque l'anneau $A$ est commutatif, l'ensemble des matrices carrées $M n (A)$ est donc muni d'une structure d'algèbre associative et unitaire avec l'addition matricielle, le produit par un scalaire et le produit matriciel.

On appelle matrice scalaire une matrice de la forme $a I n$ où $a$ est un élement de l'anneau $K$ .

aI_n=\begin{pmatrix} a & 0 & \dots & 0\\ 0 & a & \dots & 0\\ \vdots &\vdots&\ddots& 0\\ 0 & 0&\dots & a \end{pmatrix}

Ces matrices s'appellent matrices scalaires car elles se comportent comme des scalaires, vis-à-vis de la mutliplication :

Lorsque $A$ est commutatif, ou à défaut, losque $a$ est central dans $A$ , c'est-à-dire lorsque $a$ commute avec tous les éléments de $A$ , on a

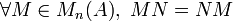
Réciproquement, toute matrice $N$ de $M n (A)$ telle que $\forall M\in M_n(A),\ MN = NM$ est une matrice scalaire $a I n$ où $a$ est central dans $M$ . Ceci se démontre en prenant pour M les matrices de la base canonique.

Une matrice de la forme :

\begin{pmatrix} a_1 & 0 & \dots & 0\\ 0 & a_2 & \dots & 0\\ \vdots &\vdots&\ddots& 0\\ 0 & 0&\dots & a_n \end{pmatrix}

sera dite matrice diagonale.

Outre le déterminant, une autre fonction à noter est la trace. Toutes deux apparaissent dans un objet plus général, le polynôme caractéristique, qui a sont tour permet d'obtenir certaines caractérisations des matrices diagonalisables (c'est-à-dire semblable (voir ci-dessous) à une matrice diagonale), ou de la trigonalisation.

Actions du groupe linéaire

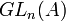
Il existe plusieurs manières de faire agir le groupe linéaire $\displaystyle GL_n(A)$ sur les espaces de matrices, et notamment :

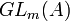
action par multiplication à gauche de $\displaystyle GL_m(A)$ sur $M m, n (A)$ , qui à P et M, associe PM,
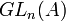
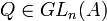
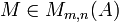
action (à droite) par multiplication à doite de $\displaystyle GL_n(A)$ sur $M m, n (A)$ , qui à $Q\in\displaystyle GL_n(A)$ et $M\in M_{m,n}(A)$ , associe $M Q$ ,
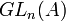
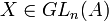
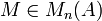
action par conjugaison de $\displaystyle GL_n(A)$ sur $M n (A)$ , qui à $X\in\displaystyle GL_n(A)$ et $M\in M_n(A)$ , associe $X M X - 1$ .

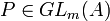
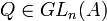
On décrit maintenant les résultats classiques sur ces actions, lorsque les scalaires forment un corps commutatif. Les deux premières actions sont souvent considérées simultanément ; on s'intéresse donc à la question : deux matrices M₁ et M₂ de dimension (m,n) étant données, existe-t-il des matrices $P\in\displaystyle GL_m(A)$ et $Q\in\displaystyle GL_n(A)$ telles que $M 1 = P M 2 Q$ ? Si tel est le cas, les deux matrices M₁ et M₂ sont dites équivalentes. Le résultat principal est que deux matrices sont équivalentes si et seulement si elles ont même rang, ce qui s'exprime encore en disant que le rang est un invariant complet pour les doubles classes définies par les deux actions de multiplication à gauche et à droite. Par ailleurs, une matrice étant donnée, on peut trouver d'autres matrices privilégiées (les matrices échelonnées) dans la même orbite pour une de ces actions par la méthode du pivot de Gauss.

Pour l'action par conjugaison, deux matrices carrées M₁ et M₂ de taille n dans la même orbite admettent une relation de la forme $M 1 = P M 2 P - 1$ , pour une certaine matrice P inversible de taille n ; deux telles matrices sont dites semblables. La description d'un système complet d'invariants est plus délicate. On appelle ces invariants les invariants de similitude. D'un point de vue algorithmique, la réduction d'une matrice quelconque à une matrice sous une forme privilégiée se fait par un algorithme inspiré de celui du pivot de Gauss, voir théorème des facteurs invariants.

Interprétations linéaires

Un intérêt principal des matrices est qu'elles permettent d'écrire commodément les opérations habituelles de l'algèbre linéaire, avec une certaine canonicité.

Coordonnées

Le premier point est de remarquer que le A-module Aⁿ s'identifie canoniquement à l'espace de matrices colonnes $M n,1 (A)$ : si e_i est le n-uplet dont tous les coefficients sont nuls, sauf le i-ème qui vaut 1, on lui associe la matrice colonne élémentaire dont tous les coefficients sont nuls sauf le i-ème qui vaut 1, et on étend l'identification par linéarité ; la matrice associée à chaque n-uplet sera appelée matrice coordonnée canonique.

D'autres identifications sont cependant possibles ; lorsqu'on peut parler de base (si l'anneau des scalaires est un corps, ou est principal, par exemple), on peut associer les matrices colonnes élémentaires à n'importe quelle base de l'espace A_n (ou plus généralement d'un A-module libre), puis à nouveau étendre par linéarité ; les matrices associées seront appelées matrices coordonnées dans la base envisagée.

On peut concaténer les matrices coordonnées, dans une base fixée, de plusieurs n-uplets. On obtient ainsi la matrice coordonnée d'une famille de vecteurs. Le rang de la matrice est alors défini comme la dimension de la famille de ces vecteurs. En particulier la matrice d'une base dans une autre base est appelée matrice de passage entre ces deux bases, ou matrice de changement de base. Si X et X' sont les matrices coordonnées du même vecteur dans deux bases B et C, et que P est la matrice de la base C dans la base B, on a la relation :

Applications linéaires

Soit $E$ et $F$ deux $A$ -module (à gauche) libres de dimensions finies. Soit B=(e₁,...,e_p) une base de $E$ et C=(f₁,...,f_n) une base de $F$ . Soit enfin $φ$ une application linéaire de $E$ dans $F$ .

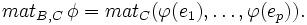
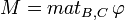
On appelle matrice de $φ$ dans le couple de bases (B,C) la matrice : $mat_{ B, C}\,\phi = mat_{C}(\varphi(e_1),\dots,\varphi(e_p)).$ L'application de $\mathcal L(E,F)$ dans $M n, p (A)$ qui à $\varphi$ associe la matrice : $M=mat_{ B, C}\, \varphi$ est un isomorphisme.

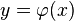
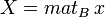
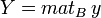
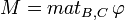
Soit x un vecteur de E. Notons $y=\varphi(x)$ , $X=mat_{B}\,x$ , $Y=mat_{ B}\,y$ et $M=mat_{ B, C}\,\varphi$ . Lorsque l'anneau A est commutatif (ou si on travaille avec des modules à droite), ces matrices sont reliées par :

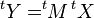
Cette formule devient $^tY=^t\!\!M\,^tX$ pour des modules à gauche sur un anneau non commutatif.

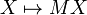
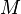
L'application $X\mapsto MX$ du $A$ -module $M p,1 (A)$ dans le $A$ -module $M n,1 (A)$ est linéaire et sa matrice dans les bases canoniques est $\displaystyle M$ . C'est un point clef du lien entre algèbre linéaire et matrices.

En conséquence, il arrive souvent qu'on l'identifie avec l'application linéaire ci-dessus. On parlera alors de noyau de la matrice, d'espaces propres de la matrice, d'image de la matrice, etc.

Si $E$ et $F$ sont deux $A$ -modules, B et B' deux bases de E, de cardinal p, et C et C' deux bases de F de cardinal n, P la matrice de B' dans B et Q la matrice de C' dans C, alors les deux matrices M et M' d'une même application linéaire $\varphi$ de $E$ dans $F$ , dans les couples de bases (B,C) et (B',C') sont liées par la relation :

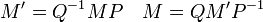
On constate ainsi que deux matrices équivalentes, d'après la définition donnée plus haut dans l'article, sont deux matrices qui représentent la même application linéaire dans des bases différentes.

En particulier, dans le cas d'un endomorphisme, si on impose B= B' et C=C' , les formules précédentes se simplifient :

On constate ainsi que deux matrices semblables, d'après la définition donnée plus haut dans l'article, sont deux matrices qui représentent le même endomorphisme dans des bases différentes.

Interprétations bilinéaires

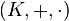
Dans ce paragraphe, l'anneau commutatif des scalaires sera noté $(K,+,\cdot)$ . Dans la plupart des applications, ce sera un corps commutatif.

Le cas non commutatif existe aussi mais il faut prendre quelques précautions et les notations deviennent trop lourdes pour cet article.

Matrice d'une forme bilinéaire

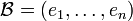
Soit $E$ un $K$ -module libre et $\mathcal B=(e_1,\dots,e_n)$ une base de $E$ .

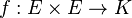
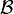
Soit $f : E\times E \to K$ une forme bilinéaire. On définit la matrice de $f$ dans la base $\mathcal B$ par la formule suivante :

mat_{\mathcal B}\, f = (f(e_i,e_j))_{1\le _i\le n,\ 1\le j\le n}= \begin{pmatrix} f(e_1,e_1) & f(e_1,e_2) & \dots & f(e_1,e_n)\\ f(e_2,e_1) & f(e_2,e_2) & \dots & f(e_2,e_n)\\ \vdots & \vdots & \ddots & \vdots\\ f(e_n,e_1) & f(e_n,e_2) & \dots & f(e_n,e_n)\\ \end{pmatrix}

Dans le cas particulier où $K=\R$ et $f$ est un produit scalaire, cette matrice est appelée matrice de Gram.

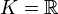
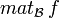
$mat_{\mathcal B}\, f$ est symétrique (respectivement antisymétrique) si et seulement si $f$ est symétrique (respectivement antisymétrique).

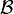
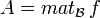
Soit $x$ et $y$ deux vecteurs de $E$ . Notons $X$ et $Y$ leurs coordonnées dans la base $\mathcal B$ et $A=mat_{\mathcal B}\, f$ . On a alors la formule : $f (x, y) = t X A Y$ .

Deux formes bilinéaires sont égales si et seulement si elles ont la même matrice dans une base donnée.

Matrice d'une forme quadratique

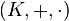
Lorsque $(K,+,\cdot)$ est un corps de caractéristique différente de 2, on appelle matrice d'une forme quadratique la matrice la matrice de la forme bilinéaire symétrique dont est issue la forme quadratique.

Formule de changement de base

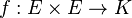
Soit $E$ un $K$ -module libre, $\mathcal B$ et $\mathcal C$ deux bases de $E$ . Soit $f : E\times E \to K$ une forme bilinéaire.

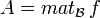
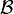
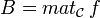
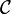
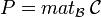
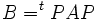
Notons $A = mat_{\mathcal B}\, f$ la matrice de $A$ dans la base $\mathcal B$ et $B = mat_{\mathcal C}\, f$ la matrice de $A$ dans la base $\mathcal C$ . Notons $P =mat_{\mathcal B}\, \mathcal C$ la matrice de passage. On a alors : $\displaystyle B=^tPAP$

Matrices congruentes

Deux matrices carrées $A$ et $B$ sont dites congruentes s'il existe une matrice inversible $P$ telle que $A = t P B P$ .

Deux matrices congruentes sont deux matrices qui représentent la même forme bilinéaire dans deux bases différentes.

Lorsque $(K,+,\cdot)$ est un corps de caractéristique différente de 2, toute matrice symétrique est congruente à une matrice diagonale. L'algorithme utilisé s'appelle réduction de Gauss à ne pas confondre avec le pivot de Gauss.

Matrices orthogonales

Matrices unitaires

Matrices symétriques

Matrices antisymétriques

Matrice d'une forme sesquilinéaire

Matrices hermitiennes

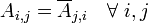
Une matrice $A$ est dite hermitienne si $A_{i,j} = \overline{A}_{j,i} \quad \forall \ i,j$ .

Exemple

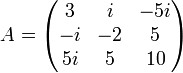
$A=\begin{pmatrix}3&i&-5i\\-i&-2&5\\ 5i&5&10\end{pmatrix}$ est une matrice hermitienne.

Décomposition d'une matrice

On utilise abusivement le terme décomposition d'une matrice, qu'il s'agisse d'une véritable décomposition (en somme) comme dans la décomposition de Dunford ou d'une factorisation comme dans la plupart des autres décomposition.

Réduction d'une matrice carrée

Réduire une matrice, c'est trouver une matrice qui lui est semblable le plus simple possible.
Une matrice diagonalisable est une matrice semblable à une matrice diagonale.

$A$ est diagonalisable si et seulement si il existe une matrice inversible $P$ et une matrice diagonale $D$ telles que $A = P - 1 D P$ .

Sur un corps algébriquement clos, on dispose de la réduction de Jordan qui est optimale et il existe des décompositions intermédiaires comme la décomposition de Dunford qui utilise les sous-espaces caractéristiques ou celle de Froebenius qui utilise les sous-espaces cycliques.
Les polynômes d'endomorphismes jouent un rôle crucial dans les techniques de réduction.

Décomposition LU

C'est une factorisation en produit de deux matrices triangulaires.
En lien avec le pivot de Gauss, c'est une méthode qui permet d'inverser une matrice.

Décomposition QR

C'est un résultat sur les matrices à coefficients réels ou à coefficients complexes.
C'est une factorisation en produit d'une matrice orthogonale et d'une matrice triangulaire.
C'est une traduction matricielle du procédé de Gram-Schmidt.

Décomposition polaire

C'est un résultat sur les matrices à coefficients réels ou à coefficients complexes.
C'est une factorisation en produit d'une matrice orthogonale et d'une matrice symétrique strictement positive dans le cas réel, en produit d'une matrice unitaire et d'une matrice hermitienne strictement positive dans le cas complexe.
On peut décomposer à droite ou à gauche.
On a unicité de la factorisation pour les matrices inversibles.

Normes et rayon spectral

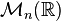
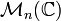
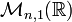
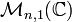
Dans tout ce paragraphe, les matrices considérées sont dans $\mathcal M_n(\R)$ ou $\mathcal M_n(\mathbb C)$ . De plus on identifie une matrice $A$ avec l'endomorphisme de $\mathcal M_{n,1}(\R)$ ou $\mathcal M_{n,1}(\mathbb C)$ qui à la matrice colonne $X$ associe la matrice colonne $A X$ . Le cas réel et le cas complexe sont identiques.

Normes et normes d'algèbre

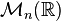
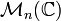
Soit $N$ une norme sur $\mathcal M_n(\R)$ ou $\mathcal M_n(\mathbb C)$ .

On dira que $N$ est une norme d'algèbre (on dit aussi norme de Banach) si et seulement si

Certains auteurs imposent en outre que $N (I n) = 1$

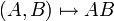
Pour une norme quelconque, l'application bilinéaire $(A,B) \mapsto AB$ étant continue (on est en dimension finie), on est assuré de l'existence d'une constante $k > 0$ telle que

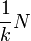
Par suite, la norme $\frac1k N$ est une norme d'algèbre. Toute norme est donc proportionnelle à une norme d'algèbre.

Rayon spectral

Soit $A$ une matrice carrée à coefficients complexes. On appelle rayon spectral le plus grand module des valeurs propres de $A$ . Dans tout ce qui suit, on notera $ρ(A)$ le rayon spectral de $A$ .

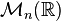
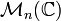
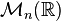
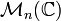
Théorème : Pour toute norme d'algèbre $N$ sur $\mathcal M_n(\R)$ (respectivement dans $\mathcal M_n(\mathbb C)$ ) et pour toute matrice $A$ dans $\mathcal M_n(\R)$ (respectivement dans $\mathcal M_n(\mathbb C)$ ), l'inégalité suivante est vérifiée :

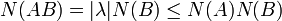
Démonstration : Soit $λ$ une valeur propre de $A$ et $X$ un vecteur propre associé. notons $B$ la matrice carrée dont la première colonne est $X$ et les autres sont nulles. On a $A B = λ B$ donc $N(AB) = |\lambda| N(B)\le N(A)N(B)$ et on peut simplifier par $N (B)$ car le vecteur $X$ étant non nul, il en est de même de la matrice $B$ .

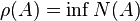
De plus, on montre que $\rho(A) = \inf N(A)$ , la borne inférieure étant prise sur l'ensemble des normes subordonnées, donc a fortiori sur l'ensemble des normes d'algèbre.

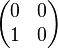
Par contre, l'égalité peut s'évérer impossible. Il suffit pour cela de considérer une matrice non nulle dont le rayon spectral est nul : $\begin{pmatrix} 0 & 0\\ 1 & 0 \end{pmatrix}$

Normes subordonnées

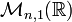
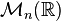
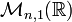
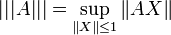
Lorsqu'on munit $\mathcal M_{n,1}(\R)$ d'une norme $\|.\|$ , on munit automatiquement $\mathcal M_n(\R)$ d'une norme, appelée norme subordonnée à $\|.\|$ . Elle est donnée par la formule suivante donnée pour une matrice $A$ quelconque dans $\mathcal M_{n,1}(\R)$ : $|||A ||| = \sup _{\|X\|\le 1} \|AX\|$

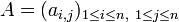
En notant $A=(a_{i,j})_{1\le i\le n,\ 1\le j\le n}$ , on a

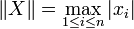
Si $\|X\| = \max_{1\leq i \leq n} |x_i|$ , (norme infinie), alors la norme de $A$ vaut :

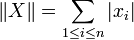
Si $\|X\| = \sum _{1\leq i \leq n} |x_i|$ , (norme indice 1), alors la norme de $A$ vaut :

Toute norme subordonnée est une norme d'algèbre avec en plus $| | | I n | | | = 1$ .

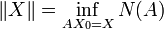
Démontrer la réciproque ou insérer contre-exemple pour la réciproque. Pour la réciproque, on pourrait construire $\|X\| = \inf_{AX_0=X} N(A)$ mais je n'ai pas vérifié que ça marche.

D'autre part, si deux normes subordonnées sont égales, les normes auxquelles celle-ci sont subordonnées sont proportionnelles. C'est une conséquence immédiate du théorème de Hahn-Banach.

Norme subordonnée à la norme euclidienne

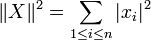
On se place dans la cas où $\mathcal M_{n,1}(\R)$ est muni de sa norme euclidienne canonique donnée par $\|X\|^2 = \sum _{1\leq i \leq n} |x_i|^2$ .

Lorsque $A$ est une matrice symétrique (respectivement hermitienne), la norme de $A$ est égale au rayon spectral de $A$ .

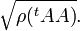
Dans le cas où $A$ est une matrice quelconque, la norme de $A$ est égal à $\sqrt {\rho(^tAA)}.$

La norme de $A$ est donc la plus grande des valeurs singulière de $A$ (les valeurs singulière de $A$ sont, par définition, les racines carrées des valeurs propres de $t A A$ ).

Exponentielle d'une matrice

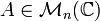
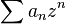
Soit $A\in\mathcal M_n(\mathbb C)$ , Soit $N$ une norme d'algèbre et $\sum a_n z^n$ une série entière de rayon de convergence $R$ .

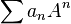
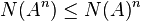
Alors si $N (A) < R$ , la série $\sum a_n A^n$ est absolument convergente. La ruse, c'est que $N(A^n)\le N(A)^n$ .

En particulier, on peut définir, pour toute matrice carrée complexe, la quantité

Le calcul effectif de cette exponentielle se fait par réduction de la matrice.

L'exponentielle joue un rôle central dans l'étude des systèmes linéaires d'équations différentielles.

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️

Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜

Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️

Cette vitamine développe les fonctions cognitives du cerveau 🧠

Comment des impacts géants vaporisent les corps planétaires ☄️

Les Américains riches vivent moins longtemps que les Européens pauvres 💰

Attention à ce riz naturellement riche en arsenic 🍚

L'intelligence artificielle contre la mort subite 💀

L'inévitable formation d'un océan de magma basal sur Terre 🔥

Découverte d'une plante étrange sans chlorophylle 🌱

Existe-t-il des mélodies naturelles ? 🎶

Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽

L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡

Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺

Imprimer en 3D avec la lumière du soleil ☀️

La pollution atmosphérique nuit gravement au cerveau 🧠

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

La physique révèle les secrets d'un strike parfait au bowling 🎳

Le TDAH associé à la démence 🧠

Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️

Le régime cétogène montre des surprises sur le cholestérol 🧐

Un tango observationnel révèle une Super-Terre 🔭

Cette expérience montre que la graisse brune augmente fortement la longévité 🕒

Page générée en 0.236 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise