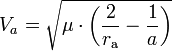Satellite artificiel - Définition
La liste des auteurs de cet article est disponible ici.
Principes physiques
Mise en orbite
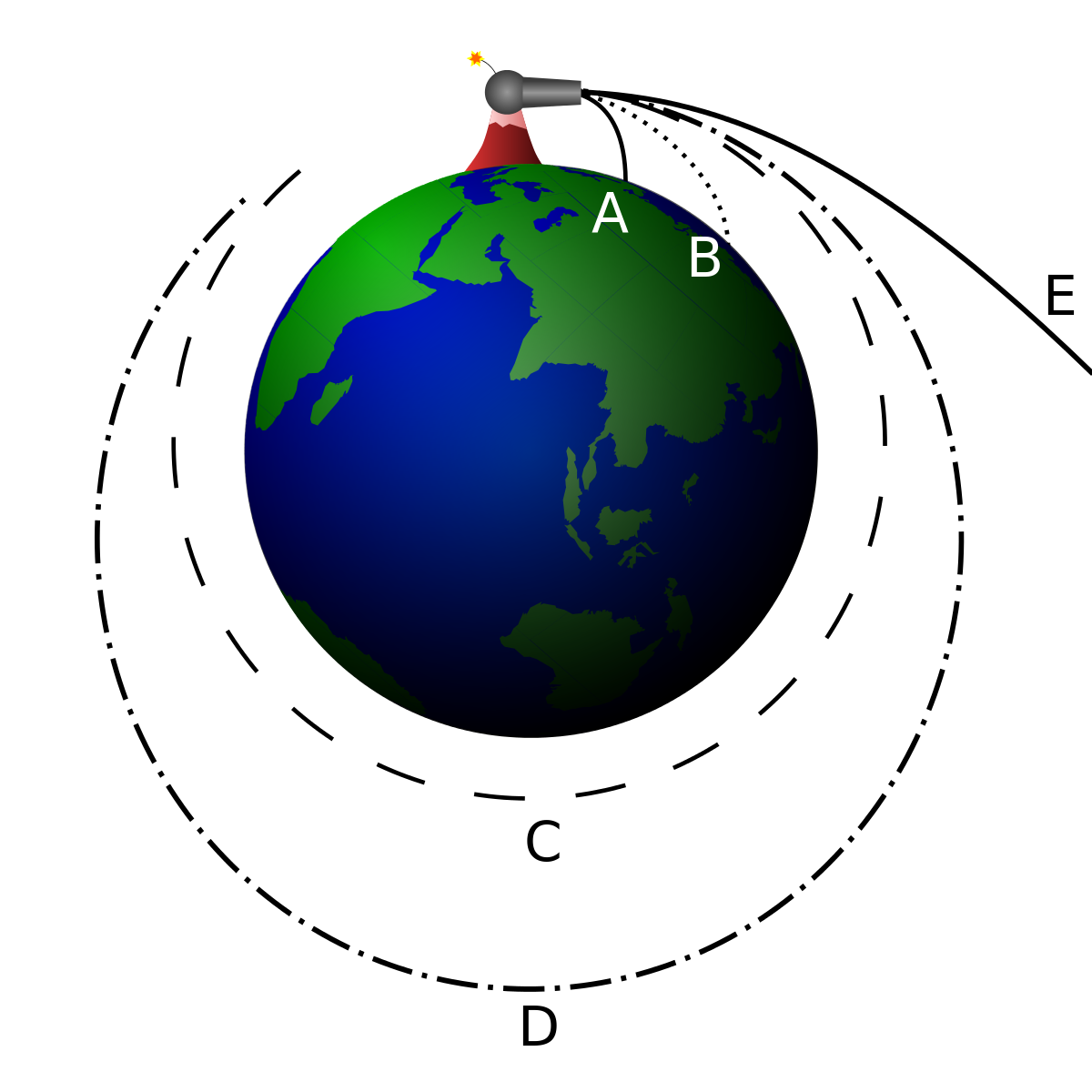
Un objet lancé à la surface de la Terre décrit une trajectoire parabolique qui le ramène au sol sous l'influence de la gravité terrestre (cas A sur le schéma). Plus la vitesse initiale de l'objet est importante plus le point de chute est éloigné (cas B). Lorsqu'une certaine vitesse est atteinte, l'objet chute mais sans jamais atteindre le sol du fait de la courbure de la Terre (cas C). Pour que l'objet conserve indéfiniment sa vitesse, il faut toutefois que celui-ci se déplace dans le vide au-dessus de l'atmosphère, là où aucune force de traînée (frottement) ne s'exerce : à cette altitude en application du principe d'inertie aucune énergie n'est en effet nécessaire pour maintenir son mouvement.
Pour qu'un objet soit satellisé autour de la Terre il faut que sa vitesse horizontale par rapport au centre la Terre (la vitesse d'injection) soit de 7 700 mètres par seconde pour une orbite circulaire à 200 km au-dessus de la Terre (au-dessous de cette altitude la traînée est trop importante). Si on communique une vitesse supérieure à un satellite circulant à la même altitude, l'orbite devient elliptique (cas D sur le schéma) : le point de l'ellipse le plus rapproché de la Terre est le périgée et le point le plus éloigné est l'apogée. Si la vitesse dépasse 11 km par seconde (cas E), le satellite échappe à l'attraction terrestre : c'est la vitesse de libération de la Terre qu'il est nécessaire de communiquer à une sonde spatiale pour qu'elle puisse être envoyée vers d'autres planètes du système solaire.
La vitesse de satellisation minimale est proportionnelle à la gravité - et donc à sa masse - du corps céleste autour duquel le satellite doit orbiter : un objet qui décolle du sol lunaire a besoin d'une vitesse horizontale beaucoup plus faible pour être satellisé (4 fois plus faible que la Terre : 1,7 km/s).
| Périgée (km) | Vitesse d'injection (km/seconde) | Remarque | Apogée atteint (km) | Type d'orbite |
|---|---|---|---|---|
| 200 | 7,78 | Vitesse minimale de satellisation | 200 | Basse (orbite circulaire) |
| 200 | 8 | 1 000 | Basse | |
| 200 | 9,2 | 10 000 | Moyenne | |
| 200 | 10,2 | 36 000 | Géosynchrone | |
| 200 | 10,8 | 380 000 | Lune | |
| 200 | 11 | Vitesse de libération | infini | interplanétaire |
Les trois lois de Kepler
La trajectoire d'un satellite artificiel ou naturel est régie par les 3 lois formulées par Kepler s'appliquant au déplacement d'un objet gravitant autour d'un corps céleste :
- loi I : l’orbite du satellite a la forme d’une ellipse dont un des deux foyers se trouve au centre du corps céleste (par exemple la Terre) autour duquel il gravite ; une orbite circulaire est un cas particulier de l’ellipse dont les deux foyers sont confondus au centre de la Terre. La forme de l'ellipse peut être définie par :
-
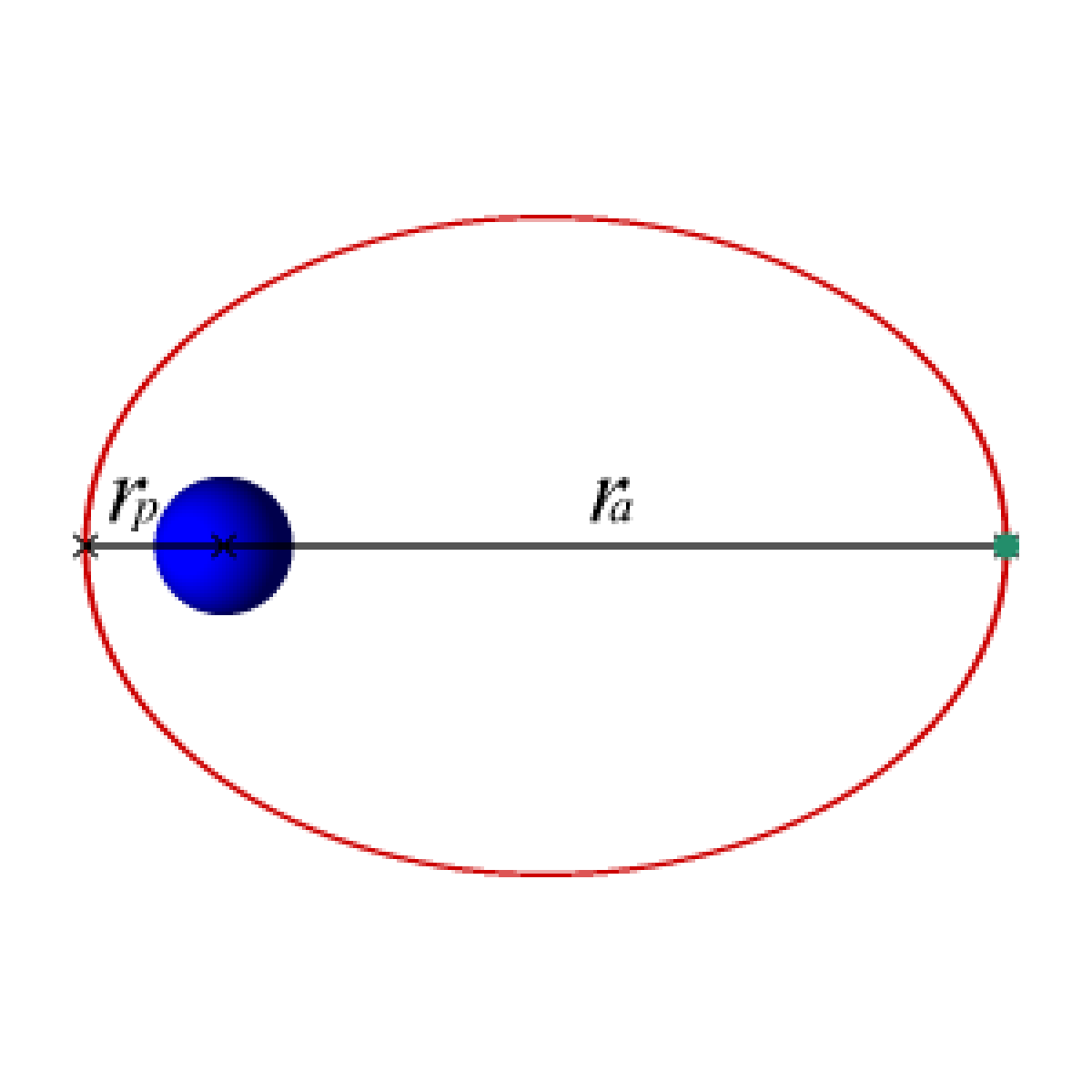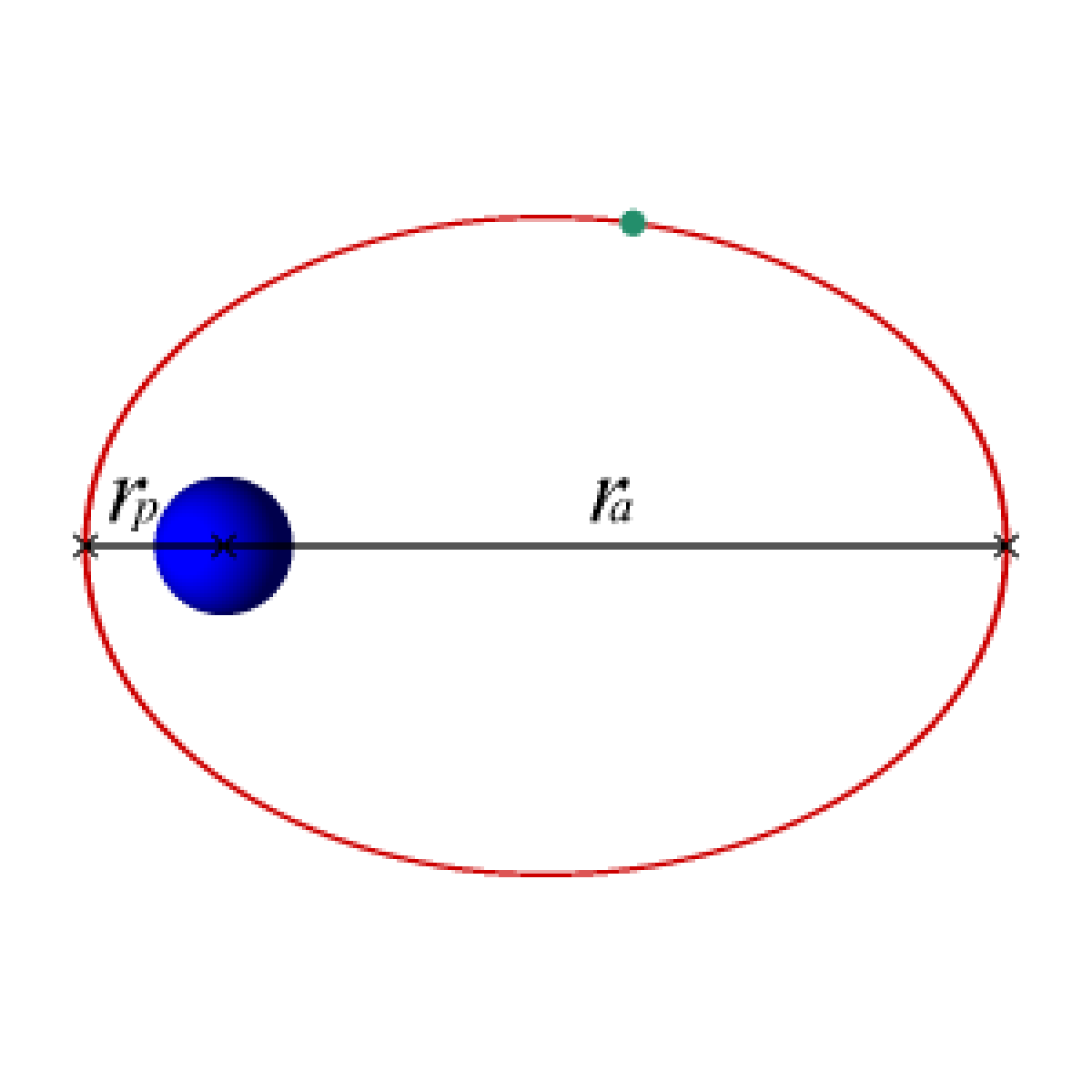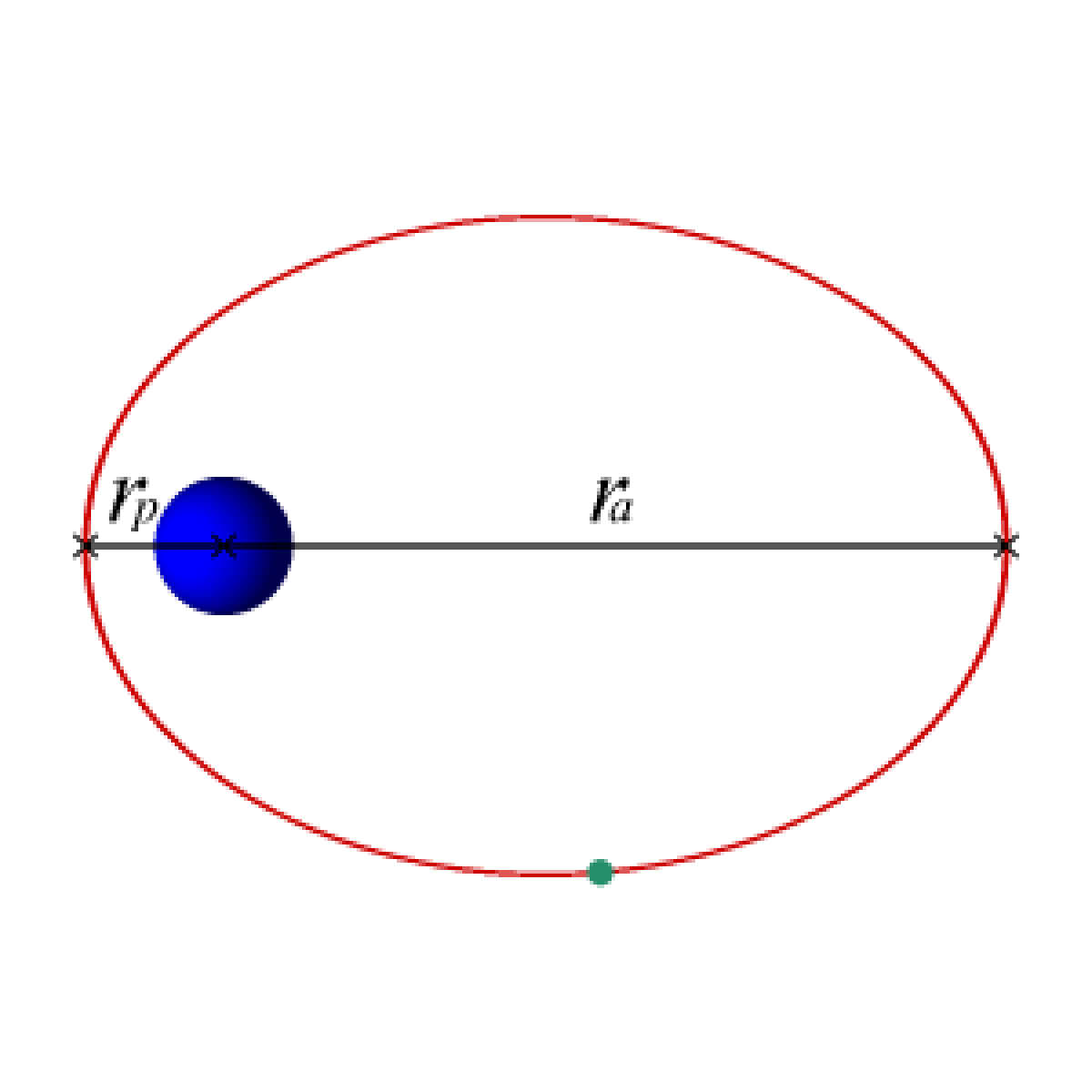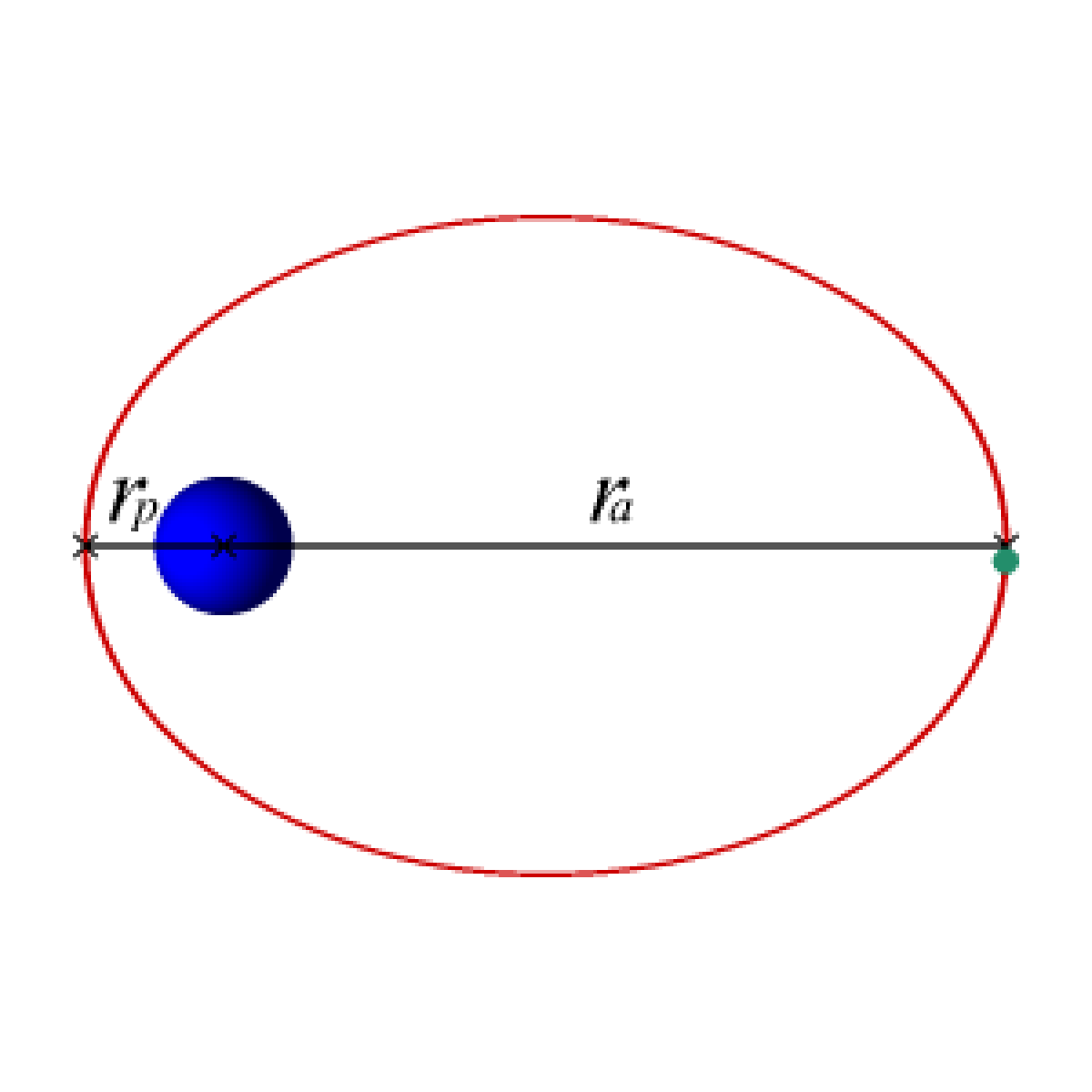
- la distance rp du point de l'orbite le plus proche de la Terre (le périgée) au centre de la Terre,
- la distance ra du point de l'orbite le plus éloigné de la Terre (l'apogée) au centre de la Terre,
- On utilise généralement à la place :
- le demi-axe a défini par la formule 2a = rp + ra,
- l'excentricité e qui définit l'allongement de l'ellipse et peut être calculée par la formule e = 1-rp/a. Elle prend une valeur comprise entre 0 et 1 : 0 correspond à une orbite circulaire et plus la valeur est proche de 1 plus l'orbite est allongée ;
- loi II : le satellite se déplace d’autant plus vite qu’il est proche du corps céleste ; plus précisément la droite qui joint le centre du corps céleste au satellite balaie toujours une aire égale dans un intervalle de temps donné ;
- loi III : le carré de la période de rotation du satellite autour du corps céleste varie comme le cube de la longueur du grand axe de l’ellipse. Si l’orbite est circulaire, le grand axe est alors le rayon du cercle.
Période et vitesse orbitale d'un satellite artificiel terrestre
Les lois de Kepler permettent de calculer à partir des caractéristiques de son orbite la période orbitale qui est l'intervalle de temps compris entre deux passages consécutifs d'un satellite par un point de son orbite, ainsi que la vitesse orbitale qui correspond à la vitesse du satellite par rapport au centre de la planète (le référentiel utilisé garde une orientation fixe dans l'espace) :
|
- Période orbitale P du satellite (en secondes)
-
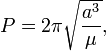
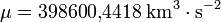
- pour une orbite elliptique de 36 000 km sur 200 km le demi-axe a est égal à 24 478 km et la période P est d'environ 138 113 secondes ;
- la formule fonctionne également pour une orbite circulaire a, étant alors remplacé par le rayon de l'orbite. Pour une orbite de 200 km le rayon est égal à 6 578 km (arrondi) ce qui donne une périodicité de 5 310 secondes soit environ 89 minutes ;
- la période augmente au fur et à mesure que l'orbite s'élève.
- un satellite en orbite géostationnaire, c'est-à-dire qui semble rester immobile à la verticale de l'équateur, a une période égale à 24 heures.
- Vitesse à l'apogée et au périgée
- pour une orbite elliptique de 36 000 km sur 200 km, r = 36 000 + 6 378 (rayon de la Terre) km et la formule permet de calculer que la vitesse à l'apogée est de 1,59 km/s ;
- la formule est la même pour le périgée (on remplace r par r). On obtient dans le cas ci-dessus une vitesse de 10,24 km/s ;
- pour une orbite circulaire la vitesse est constante (on remplace ra par le rayon de l'orbite). Pour une orbite de 200 km, la vitesse est égale à 7,784 km/s.
- un satellite en orbite géostationnaire, c'est-à-dire qui semble rester immobile à la verticale de l'équateur, a une vitesse d'environ 3 km/s.
- Il ne faut pas confondre cette vitesse avec celle qu'il est nécessaire d'imprimer au satellite pour atteindre son orbite : cette dernière est en partie transformée en énergie potentielle gravitationnelle.
Les paramètres de l'orbite d'un satellite
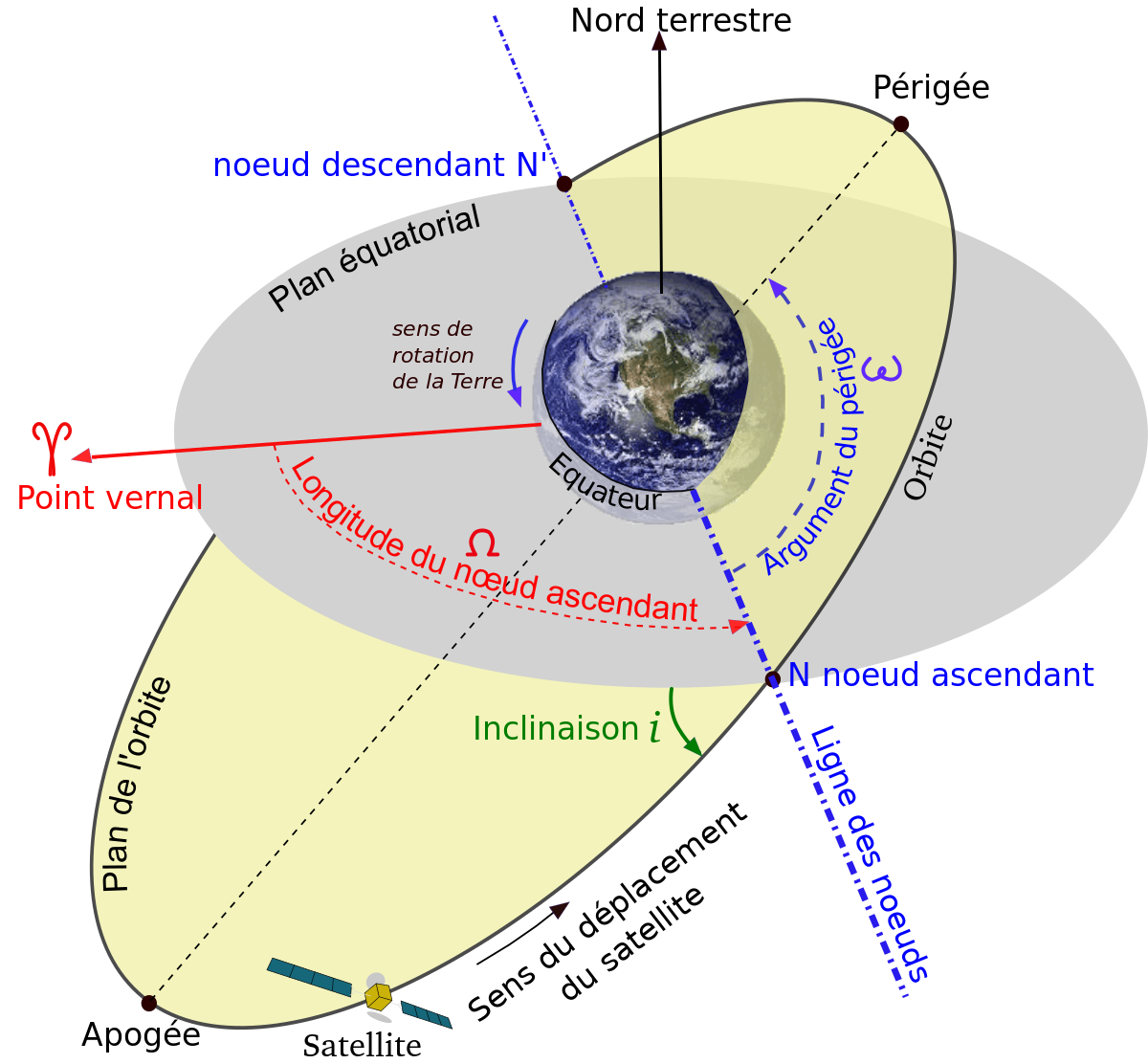
Six paramètres sont utilisés pour fournir la position et la trajectoire d'un satellite dans l'espace :
- l'orbite d'un satellite est un plan. Si on ne tient pas compte des perturbations naturelles auxquelles elle est soumise et en l'absence de manœuvres du satellite, le plan d'orbite est fixe dans l'espace. Ce plan peut être défini par deux paramètres : l'inclinaison i et la longitude (ou ascension droite) du nœud ascendant ☊ ;
- trois paramètres – l'excentricité e et le demi-grand axe a de l'ellipse ainsi que l'argument du périgée ω – permettent de décrire la trajectoire en forme d'ellipse dans le plan d'orbite ;
- un dernier paramètre permet de situer le satellite sur son orbite : on peut par exemple prendre le temps t écoulé depuis le passage au périgée.
- Plans et droites de référence
Les paramètres de l'orbite sont définis dans un référentiel constitué de plusieurs plans et de droites :
- la trajectoire de la Terre autour du Soleil s'inscrit dans un plan, dit plan de l'écliptique, passant par le centre du Soleil ;
- le plan de l'équateur terrestre est le plan passant à la latitude de l'équateur ;
- à l'équinoxe de printemps le 21 mars le plan de l'équateur terrestre coupe le plan de l'écliptique selon une ligne dite ligne des équinoxes passant par le Soleil. Cette droite qui désigne à l'infini le point vernal γ est fixe dans le système solaire ;
- l'orbite d'un satellite coupe le plan de l'équateur en deux points appelés nœud ascendant lorsque le satellite passe de l'hémisphère sud à l'hémisphère nord et nœud descendant. La ligne reliant les deux points est appelée ligne des nœuds.
- L'orientation du plan de l'orbite
L'inclinaison i du plan de l'orbite du satellite (entre 0 et 180 degrés) est l'angle que fait le plan de l'orbite avec le plan de l'équateur. Lorsque i = 90° l'orbite du satellite survole les pôles (orbite polaire) ; si i = 0 le plan de l'orbite se situe dans le plan de l'équateur. L'orbite est dite directe lorsque i est inférieur à 90° et rétrograde sinon.
La longitude du nœud ascendant ☊ (ou ascension droite du nœud ascendant) est l'angle entre la direction du point vernal et la ligne des nœuds, dans le plan de l'écliptique. Si le plan de l'orbite coïncide avec la droite des équinoxes la longitude du nœud ascendant est nulle.
- Les caractéristiques de la trajectoire dans le plan d'orbite
Dans le plan défini par les paramètres précédents, l'orbite est décrite par trois paramètres. La forme de l'ellipse que parcourt le satellite est fournie par deux informations :
- le demi-grand axe a c'est-à-dire la moitié de la distance qui sépare le périgée de l'apogée ;
- l'excentricité e de l'ellipse décrite par le satellite. Si e = 0 le satellite a une orbite circulaire.
L'argument du périgée ω est l'angle formé par la ligne des nœuds et la direction du périgée (la droite passant par la Terre et le périgée de la trajectoire du satellite), dans le plan orbital. La longitude du périgée est la somme de la longitude du nœud ascendant et de l'argument du périgée.
- La position du satellite sur son orbite
La position du satellite sur sa trajectoire peut être fournie de deux manières :
- en spécifiant le temps t écoulé depuis son passage au périgée. t = 0 indique que le satellite est à son périgée ;
- en indiquant l'angle ν (dit anomalie vraie) formé par les droites allant du centre de la Terre vers d'une part le périgée et d'autre part la position du satellite. ν = 0° indique que le satellite se trouve à son périgée.
Les perturbations naturelles de l'orbite

La trajectoire d'un satellite artificiel autour d'un corps céleste n'est pas complètement stable. Elle est modifiée par plusieurs phénomènes naturels dont l'influence est variable selon le corps céleste et la position du satellite. Si celui-ci tourne autour de la Terre, les phénomènes perturbateurs sont dans l'ordre décroissant d'influence :
- l'aplatissement du corps céleste à ses pôles et le renflement équatorial ;
- les autres irrégularités du champ de gravité ;
- la résistance de l'atmosphère (en orbite basse) ;
- l'attraction de la Lune ;
- l'attraction du Soleil ;
- la pression de radiation ;
- L'aplatissement du corps céleste à ses pôles
La Terre n'a pas une forme parfaitement sphérique : ses pôles sont légèrement aplatis tandis l'équateur présente un renflement. Ces déformations induisent des modifications du plan de l’orbite. Ce mouvement, la précession nodale, est d'autant plus important que l'inclinaison de l'orbite est différente de 90° et proche de la Terre.
Cette perturbation, la plus importante que subit le satellite, modifie à la fois l'ascension droite du nœud ascendant ☊ et l'argument du périgée ω. Pour maintenir l'orbite, il est nécessaire de consommer beaucoup de carburant. Aussi les satellites en orbite basse, plutôt que de les corriger, soit exploitent les modifications d'orbite induites (satellite en orbite héliosynchrone) soit sont placés sur des orbites ayant des inclinaisons pour lesquels cette perturbation est nulle (i = 90° et 63° 26').
- Les autres irrégularités du champ de gravité
Le champ de gravité terrestre présente d'autres irrégularités que celles dues aux déformations au pôle et à l'équateur : elles sont liées à des variations de densité (réplétions) du sous-sol terrestre (croûte et manteau). Celles-ci sont particulièrement nombreuses sur la Lune. Pour les satellites terrestres les variations du champ de gravité finissent par perturber l'orbite avec un ordre de grandeur beaucoup moins important que celui dû à l'aplatissement du globe terrestre.
- La résistance de l'atmosphère
Si le corps céleste autour duquel gravite le satellite possède une atmosphère (Terre, Mars, Vénus) celle-ci exerce une force de traînée proportionnelle à la vitesse du satellite et à la densité de l'atmosphère : la vitesse du satellite est progressivement réduite. Si l'orbite est elliptique le premier effet de la résistance de l'atmosphère est de la rendre circulaire (l'apogée est modifiée et le périgée reste invariant) puis l'orbite circulaire est elle-même progressivement abaissée. Le satellite finit par être détruit en rentrant dans les couches les plus denses de l'atmosphère. Dans le cas d'un satellite tournant autour de la Terre sur une orbite circulaire sa durée de vie moyenne est égale à (compte tenu de l'impact d'un vent solaire moyen détaillé plus loin) :
- quelques jours pour une orbite de 200 km ;
- quelques semaines à 300 km ;
- quelques années à 600 km ;
- un siècle à 800 km (c'est l'orbite des satellites de télédétection, comme la famille Spot) ;
- plusieurs siècles à 1 000 km (ce sont les orbites des constellations des satellites de télécommunications, comme Globalstar et Iridium) ;
- un million d'années à 36 000 km (ce sont les satellites géostationnaires, ou ceux qui ont terminé leur service opérationnel et ont été désorbités, vers une orbite de rebut).
L'orbite des satellites artificiels circulant sur une orbite basse est généralement maintenue au-dessus de 300 km pour que leur durée de vie ne soit pas trop brève. Pour certaines applications (satellite de renseignement, application scientifique), une orbite plus basse peut être choisie de manière temporaire ou permanente pour améliorer la précision de l'observation : le satellite doit alors emporter une grande quantité de carburant pour conserver cette orbite sinon sa durée de vie est particulièrement brève. Les satellites espions américains Keyhole 9 construits dans les années 1980 pouvaient ainsi descendre à une altitude de 118 km. On peut réduire la traînée des satellites orbitant à basse altitude en leur donnant une forme aérodynamique comme dans le cas du satellite GOCE qui, pour affiner notre connaissance du champ de gravité, parcourt une orbite circulaire de 250 km.
Le vent solaire, qui est un flux de plasma constitué essentiellement d'ions et d'électrons éjectés de la haute atmosphère du Soleil, peut augmenter temporairement la traînée. Ce flux varie en vitesse et en température au cours du temps en fonction de l'activité solaire. Celle-ci suit un cycle de 11 ans. Lors des éruptions solaires le réchauffement de l’ionosphère entraîne la dilatation vers le haut des couches supérieures de l'atmosphère. Entre 300 et 500 km la densité peut être multipliée par 10 : la force de traînée augmente en proportion et certains satellites peuvent ainsi perdre plus de 10 km en quelques jours. Ces effets sont particulièrement gênants pour les satellites d’observation de la Terre tels que Spot, dont la position doit être connue avec une grande précision.
- L'attraction de la Lune et du Soleil
Les deux astres ont une influence sur la trajectoire d'un satellite artificiel. Le Soleil malgré sa taille a une influence plus faible que la Lune du fait de son éloignement. La perturbation est d'autant plus forte que l'altitude de l'apogée est élevée : elle est nulle pour les satellites en orbite basse et faible pour les satellites géostationnaires.
Les photons émis par le Soleil exercent une pression faible — de l'ordre de 10-5 Pa autour de la Terre — mais continue sur les objets qu'ils rencontrent. La force exercée est proportionnelle à la surface exposée (l'incidence et le caractère réfléchissant de la surface exposée ont une incidence sur cette force).