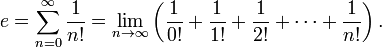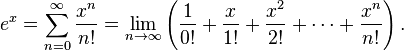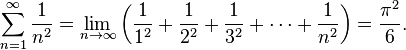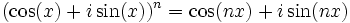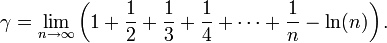Leonhard Euler - Définition

Autres sciences

Leonhard Euler a également contribué à d'autres sciences, comme certains domaines des sciences physiques, en étudiant par exemple le mouvement de la Lune.

Physique et astronomie

Euler a contribué à l'élaboration de la théorie d'Euler-Bernoulli, qui est un modèle utilisé dans le domaine de la résistance des matériaux. En dehors de l'application avec succès ses outils d'analyse aux problèmes liés à la mécanique newtonienne, Euler a également appliqué ses techniques à des problèmes d'astronomie. Ses travaux dans cette science ont été reconnus par un certain nombre de prix décernés par l'Académie de Paris au cours de sa carrière. Ses réalisations comprennent la détermination avec une grande précision des orbites des comètes et des autres corps célestes, mais aussi la compréhension de la nature des comètes, et le calcul de la parallaxe du Soleil. Ses calculs ont également contribué à l'élaboration de tables précises de longitudes.

En dynamique des fluides, Euler fut le premier à poser les équations désormais connues sous le nom d'équations d'Euler des fluides parfaits, dans « Mémoires de l'Académie royale des sciences et des belles lettres de Berlin » (1757). Elles permettent le calcul de nombreux écoulements, comme la circulation sanguine, l'aérodynamique des automobiles et des avions, l'hydraulique, l'océanographie, la météorologie ou la grande tache rouge de Jupiter.

En outre, Euler a fait d'importantes contributions en optique. Il a exprimé son désaccord avec la théorie corpusculaire de la lumière de Newton dans Opticks, qui était alors la théorie dominante. Ses documents des années 1740 sur l'optique ont contribué à faire en sorte que la théorie ondulatoire de la lumière proposée par Christian Huygens devienne la théorie la plus largement répandue, au moins jusqu'au développement de la théorie quantique de la lumière.

Logique

Il est aussi crédité pour avoir, avec l'aide des courbes fermées, illustré le raisonnement syllogistique, en 1768. Ces schémas sont désormais connus sous le nom des diagrammes d'Euler.

Aucun prêtre n'est un singe. Or, les chimpanzés sont des singes. Donc, les chimpanzés ne sont pas prêtres.

Contributions aux mathématiques

Leonhard Euler a travaillé dans presque tous les domaines des mathématiques : la géométrie, le calcul infinitésimal, la trigonométrie, l'algèbre et la théorie des nombres. Il est une figure capitale de l'histoire des mathématiques : s'ils étaient imprimés, ses écrits, dont beaucoup sont d'un intérêt fondamental, pourraient occuper entre quarante et soixante ouvrages. Le nom d'Euler est associé à un grand nombre de sujets.

Notation mathématique

Euler a introduit et popularisé plusieurs conventions de notation par le biais de ses nombreux ouvrages largement diffusés. Plus particulièrement, il a introduit la notion de fonction et a été le premier à écrire f(x) pour désigner la fonction f appliquée à l'argument x, en 1734. Il a également introduit la notation moderne des fonctions trigonométriques, la lettre e pour la base du logarithme naturel (également connue sous le nom de nombre d'Euler) en 1727, la lettre grecque Σ pour désigner une somme en 1755 et la lettre i pour représenter l'unité imaginaire, en 1777. L'utilisation de la lettre grecque π pour désigner le rapport de la circonférence d'un cercle à son diamètre a également été popularisée par Euler, mais celui-ci n'est pas à l'origine de la notation.

Analyse

Le développement du calcul infinitésimal a été au premier plan des recherches mathématiques du XVIII^e siècle, et la famille Bernoulli — amis d'Euler — est à l'origine de nombreux progrès dans ce domaine. Grâce à leur influence, l'étude du calcul infinitésimal est devenu l'un des axes principaux du travail d'Euler. Bien que certaines des démonstrations d'Euler ne soient pas acceptables au regard des normes modernes de rigueur mathématique, ses idées ont tout de même conduit à de grandes avancées.

Euler est bien connu dans le domaine de l'analyse pour son usage fréquent des séries numériques et des séries entières. Il a notamment montré que le nombre e est la somme de la série de terme général 1/n! :

Il a trouvé le « développement en série entière » de la fonction exponentielle :

et celui de la fonction Arctangente.

Sa tenacité à utiliser les développements en séries lui a permis de résoudre le fameux problème de Bâle en 1735 :

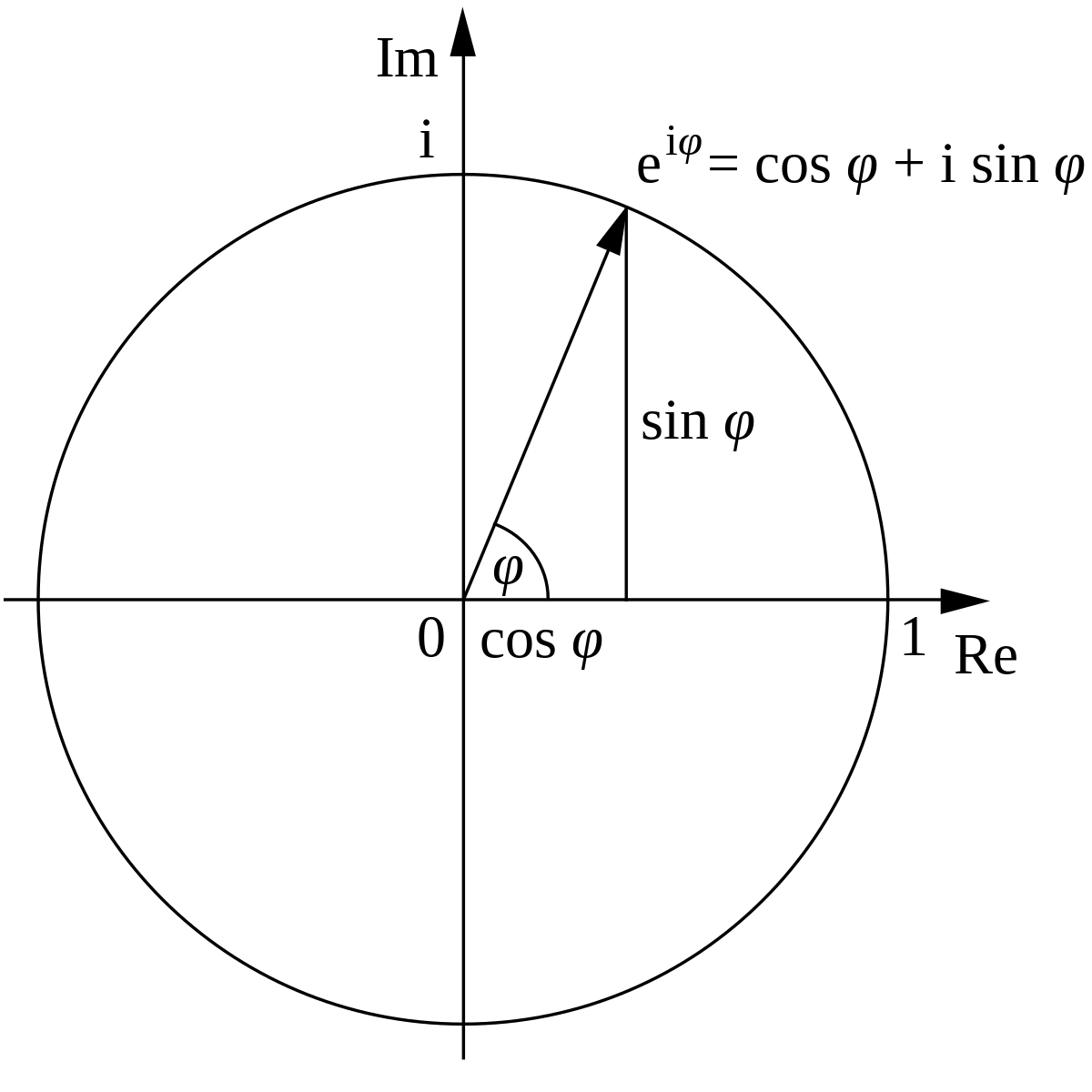
Euler a introduit l'utilisation de la fonction exponentielle et des logarithmes dans les démonstrations en analyse. Il a découvert des moyens d'exprimer différentes fonctions logarithmiques en utilisant les séries entières, et il a étendu la notion de logarithme aux nombres négatifs et aux nombres complexes. Il a également défini la fonction exponentielle pour les nombres complexes, et a découvert la relation qui la lie aux fonctions trigonométriques :

pour tout réel φ ,

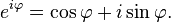
Un cas particulier de cette « formule d'Euler », obtenu en donnant à φ la valeur π est

, qu'on préfère souvent écrire :

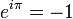
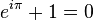
formule connue sous le nom d'identité d'Euler, et qualifiée de « formule la plus remarquable des mathématiques » par Richard Feynman, car elle réunit en seulement 7 caractères l'addition, la multiplication, l'exponentiation, l'égalité et les constantes remarquables 0, 1, e, i et π. En 1988, les lecteurs de The Mathematical Intelligencer l'ont désignée comme « la plus belle formule mathématique de tous les temps ». Au total, le nom d'Euler figurait dans trois des cinq formules arrivées en tête de ce vote.

La formule de De Moivre

est une conséquence directe de la formule d'Euler.

En outre, Euler a contribué à la théorie des fonctions transcendantes avec l'introduction de la fonction gamma. Il a également introduit une nouvelle méthode pour résoudre les équations quartiques. Il a aussi trouvé une façon de calculer des intégrales avec des limites complexes, préfigurant le développement moderne de l'analyse complexe, et a inventé le calcul des variations, qui inclut l'un de ses résultats les plus célèbres, nommé l'équation d'Euler-Lagrange.

Euler fut le pionnier de l'utilisation de méthodes d'analyse pour résoudre des problèmes de la théorie des nombres. Ce faisant, il a réuni deux branches différentes des mathématiques et introduit un nouveau champ d'étude : la théorie analytique des nombres. Euler a aussi introduit la théorie des séries hypergéométriques, des fonctions hyperboliques et la théorie analytique des fractions continues. Par exemple, il a prouvé l'infinité des nombres premiers en utilisant la divergence de la série harmonique, et il a utilisé les méthodes analytiques pour avoir une meilleure compréhension de la répartition des nombres premiers. Les travaux d'Euler dans ce domaine ont contribué à l'élaboration du théorème des nombres premiers.

Théorie des nombres

L'intérêt d'Euler dans la théorie des nombres peut être attribué à l'influence de Christian Goldbach, son ami à l'Académie de Saint-Pétersbourg. Un grand nombre des premiers travaux d'Euler en théorie des nombres est fondé sur les travaux de Pierre de Fermat. Euler a développé quelques idées de Fermat, et a réfuté certaines de ses conjectures.

Euler a fait le lien entre la distribution des nombres premiers et l'analyse. Il a démontré que la série des inverses des nombres premiers diverge. Pour ce faire, il a découvert le lien entre la fonction zêta de Riemann et les nombres premiers.

Euler a démontré les identités de Newton, le petit théorème de Fermat, le théorème des deux carrés de Fermat, et il a également travaillé sur le théorème des quatre carrés de Lagrange. Il a aussi défini la fonction φ qui associe à tout entier n le nombre d'entiers positifs inférieurs à n et qui sont premiers avec n. En utilisant les propriétés de cette « indicatrice », il a généralisé le petit théorème de Fermat pour aboutir à ce qui est maintenant connu sous le nom de théorème d'Euler. Il a contribué de manière significative à la recherche sur les nombres parfaits, qui ont fasciné les mathématiciens depuis Euclide. Euler a également fait progresser les recherches sur le théorème des nombres premiers, et il a conjecturé la loi de réciprocité quadratique. Ces deux derniers énoncés sont considérés comme des théorèmes fondamentaux de la théorie des nombres, et en cela Euler a ouvert la voie aux travaux de Carl Friedrich Gauss.

En 1772, Euler a démontré que 2³¹ − 1 = 2 147 483 647 est un nombre premier de Mersenne. Il est resté le plus grand nombre premier connu jusqu'en 1867.

Géométrie

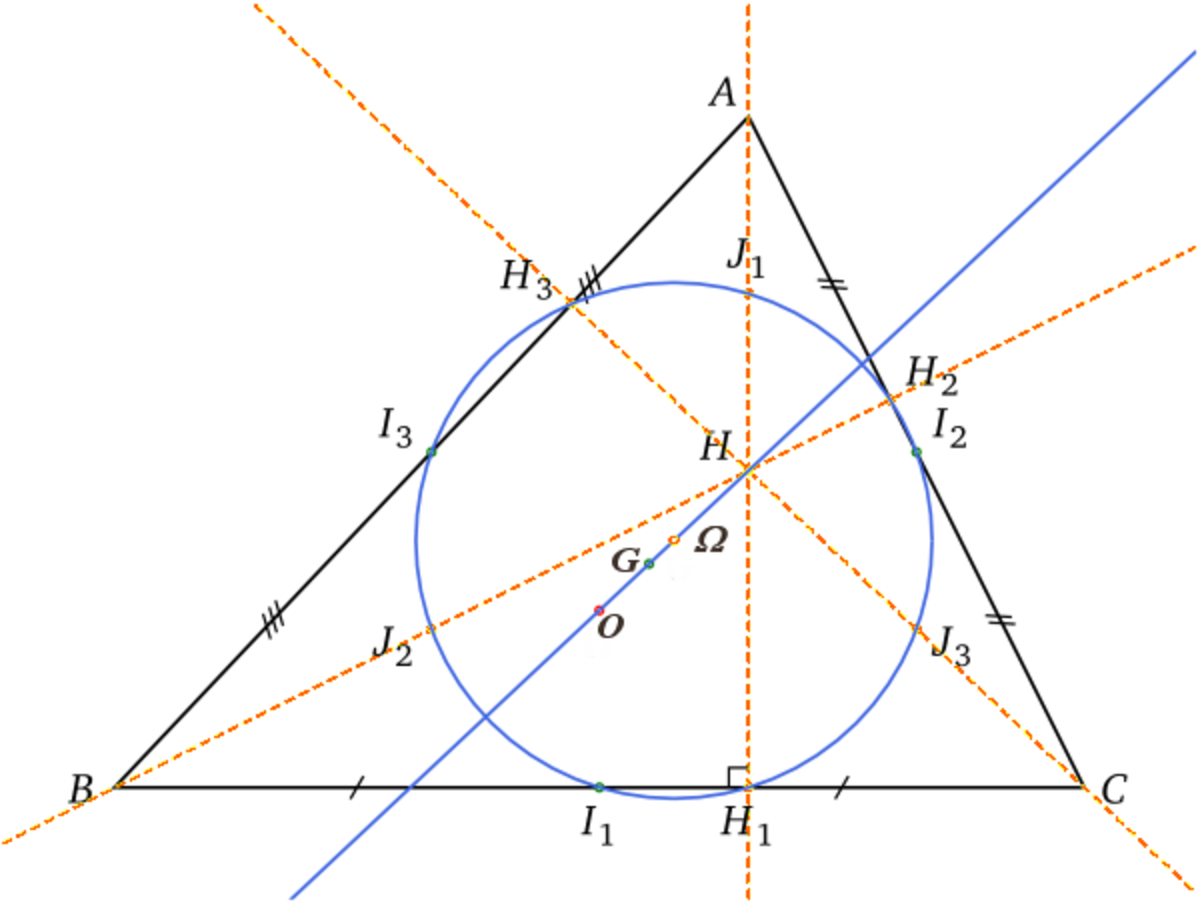
Leonhard Euler a montré que, pour tout triangle, les neuf points suivants :

• les milieux des trois côtés
• les pieds des trois hauteurs
• les milieux de chacun des segments reliant l'orthocentre aux sommets du triangle

sont situés sur un même cercle. Ce « cercle des neuf points » est encore appelé « cercle d'Euler » associé au triangle.

Il a démontré aussi que, dans tout triangle, l'orthocentre, le centre du cercle circonscrit, le centre de gravité et le centre du cercle des neuf points sont alignés. La droite qui les porte est appelée « droite d'Euler » associée au triangle.

Cercle et droite d'Euler d'un triangle quelconque

Théorie des graphes

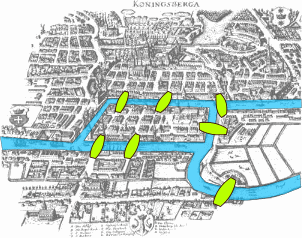
En 1736, Euler résolut le problème des sept ponts de Königsberg. La ville de Königsberg, en Prusse, est traversée par la rivière Pregolia, qui entoure deux grandes îles reliées entre elles et aux deux rives par sept ponts. Le problème était de savoir s'il est possible de suivre un chemin qui emprunte chaque pont une fois et une seule et revienne au point de départ. Euler a établi que, pour que ce soit possible, il aurait fallu que chacune des quatre zones géographiques (les deux îles et les deux rives) soit atteinte par un nombre pair de ponts — en termes modernes : que chacun des quatre « sommets » du « graphe » soit adjacent à un nombre pair d'« arêtes » (un graphe ayant cette propriété est dit « eulérien »). La résolution de ce problème est considérée comme le premier théorème de la théorie des graphes.

Euler a également établi la formule S − A + F = 2 liant le nombre de sommets, d'arêtes et de faces d'un polyèdre convexe, et donc d'un graphe planaire. La constante de cette formule est maintenant connue comme la caractéristique d'Euler pour un graphe (ou pour un autre objet mathématique), et est liée au genre de l'objet. L'étude et la généralisation de cette formule, notamment par Cauchy et L'Huillier, est à l'origine de la topologie.

En outre, Leonhard Euler est le premier à avoir étudié le problème du cavalier, en 1759. Il publiera ses recherches sur la question dans « Solution d'une question curieuse qui ne paraît soumise à aucune analyse ».

Mathématiques appliquées

Certains des plus grands succès d'Euler ont été dans la résolution des problèmes analytiques dans des domaines autres que les mathématiques et dans la description de nombreuses applications des nombres de Bernoulli, des séries de Fourier, des diagrammes de Venn, des nombres d'Euler, des constantes e et π, des fractions continues et des intégrales. Il a développé des outils qui rendent plus faciles à appliquer certains problèmes physiques. Il a fait progresser le domaine de l'amélioration de l'approximation numérique d'intégrales, en inventant ce qui est maintenant connu sous le nom de méthode d'Euler. Euler a également démontré, en même temps que l'écossais Colin Maclaurin — mais bien indépendamment — la formule d'Euler-Maclaurin. Il a aussi facilité l'utilisation des équations différentielles, en particulier en introduisant la constante d'Euler-Mascheroni :

Un des domaines les moins communs qui intéressaient Euler était l'application des idées mathématiques à la musique. En 1739, il écrivit Tentamen novae theoriae musicae, dans l'espoir de finalement intégrer la théorie musicale aux mathématiques. Cette partie de son travail, cependant, n'a pas reçu une grande attention et a été décrite comme trop mathématique pour les musiciens mais aussi trop musicale pour les mathématiciens.