Théorie des cordes - Définition
La théorie des cordes est l'une des voies envisagées pour régler une des questions majeures de la physique théorique : fournir une description de la gravité quantique c'est-à-dire l'unification de la mécanique quantique (inévitable pour décrire la physique aux petites échelles) et de la théorie de la relativité générale (nécessaire pour décrire la gravitation de manière relativiste). La principale particularité de la théorie des cordes est que son ambition ne s'arrête pas à cette réconciliation, mais qu'elle prétend réussir à unifier les quatre interactions élémentaires connues, on parle de théorie du tout, tout en reposant sur deux hypothèses assez révolutionnaires :
- Les briques fondamentales de l'Univers ne seraient pas des particules ponctuelles mais des sortes de cordelettes vibrantes possédant une tension à la manière d'un élastique. Ce que nous percevons comme des particules de caractéristiques distinctes (masse, charge électrique, etc) ne seraient que des cordes vibrant différemment. Avec cette hypothèse, les théories des cordes admettent une échelle minimale, reliée à la taille de Planck, et permettent ainsi d'éviter facilement l'apparition de certaines quantités infinies (on parle de " divergences ") qui sont inévitables dans les théories quantiques de champs habituelles.
- L'univers contiendrait plus de trois dimensions spatiales. Certaines d'entre elles, repliées sur elles-mêmes (voir les théories d'Oskar Klein), passant inaperçues à nos échelles (par une procédure appelée réduction dimensionnelle).
La théorie des cordes a obtenu des premiers résultats partiels très prometteurs. Dans le cadre de la thermodynamique des trous noirs elle permet de reproduire la formule de Bekenstein et Hawking pour l'entropie des trous noirs. Elle possède également une richesse mathématique remarquable : en particulier elle a permis de découvrir la symétrie miroir en géométrie.
Toutefois la théorie des cordes reste incomplète. D'une part, une multitude de solutions aux équations de la théorie des cordes existe, ce qui pose un problème de sélection de notre univers et, d'autre part, même si beaucoup de modèles voisins ont pu être obtenus, aucun d'entre eux ne permet de rendre compte précisément du modèle standard de la physique des particules.
Bien que différentes formulations indépendantes (cf ci-dessous) aient été développées dans les années 1980, les résultats de dualité de cordes obtenus dans les années 1990 ont permis d'envisager que toutes les théories précédemment construites ne sont elles-mêmes que différentes limites d'une théorie unique plus fondamentale, baptisée théorie M, dont la formulation microscopique reste inconnue[1] mais dont la théorie effective de basse énergie est la supergravité maximale à 11 dimensions, soit une de plus que la dimension critique des théories de supercordes.
Historique de la théorie
Genèse, une première tentative infructueuse
La théorie des cordes a d'abord été introduite comme tentative de description de l'interaction forte mais ses prédictions étaient en désaccord avec les observations expérimentales. Elle fut donc vite abandonnée au profit de la chromodynamique quantique (abrégée en QCD).
La première révolution des cordes
En 1984, par une prouesse technique remarquable, Michael B. Green et John H. Schwarz démontrent l'absence d'anomalies de jauge ou gravitationnelle dans la théorie de cordes de type I qui est une théorie chirale de même que le modèle standard. Ce travail offre pour la première fois la perspective d'obtenir une phénoménologie réaliste à partir de cordes. L'impact a été si important dans la communauté de la physique théorique que le terme de révolution a été adopté pour décrire la période de développement très rapide qui s'en est suivie.
La seconde révolution des cordes
Au milieu des années 1990, un grand nombre de ponts ou dualités sont découverts entre les différentes théories de cordes. En 1995 le physicien Edward Witten suggère que ces dualités sont la contrepartie de l'existence d'une théorie plus fondamentale, appelée théorie M réunissant de façon continue les différentes théories des cordes qui sont alors obtenues dans certaines limites de son espace des paramètres (appelé espace de modules). Cette période d'intense activité dans le domaine lui a valu le nom de seconde révolution des cordes.
Développements actuels
Plusieurs physiciens s'attachent à développer la théorie des cordes, censée unifier les quatre grandes forces qui régissent l'Univers.
La correspondance AdS/CFT
En 1997, Juan Maldacena propose une conjecture, appelée correspondance AdS/CFT qui affirme, dans sa forme la plus générale, l'équivalence complète entre une certaine théorie de jauge, la théorie de super Yang-Mills avec supersymétrie étendue N = 4 et la théorie des cordes de type IIb sur l'espace
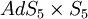
À ce jour (2006) la correspondance AdS/CFT n'a pas été démontrée mais un très grand nombre de tests très non-triviaux[réf. nécessaire] ont été effectués où la conjecture a toujours été vérifiée avec une grande précision. Ces tests consistent la plupart du temps en deux calculs effectués indépendamment dans le cadre de la théorie de jauge d'une part et dans le cadre de la théorie des cordes d'autre part et en une comparaison des deux résultats.
Cette conjecture est remarquable dans la mesure où elle établit une relation naturelle entre une théorie de jauge, par nature non-gravitationnelle, et une théorie de la gravité quantique ce qui va dans le sens d'une intuition formulée depuis longtemps par le physicien Gerard 't Hooft[réf. nécessaire].
Par ailleurs la correspondance AdS/CFT constitue une réalisation du principe holographique dans la mesure où l'espace sur lequel vit la théorie de super-Yang Mills est situé au bord de l'espace
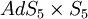
Les transitions géométriques
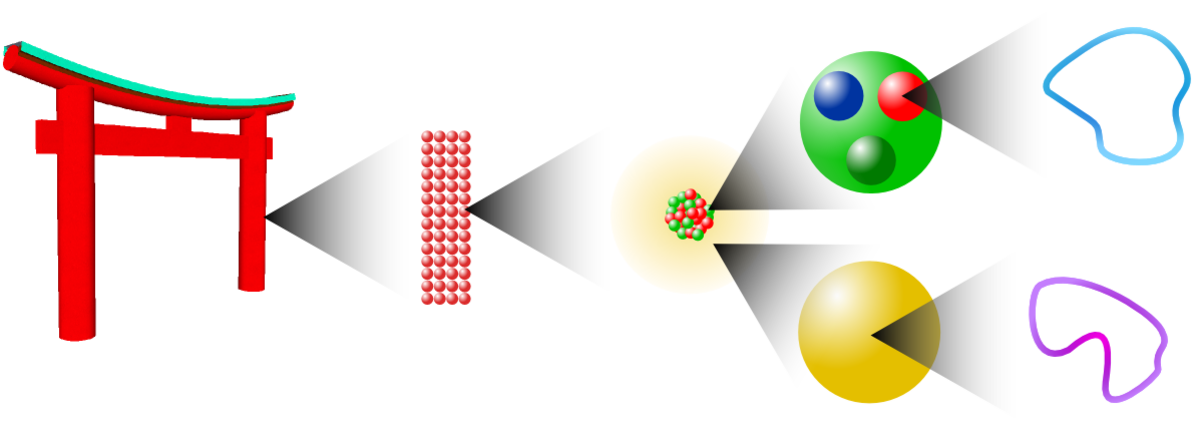
Inspirés par les succès de la conjecture AdS/CFT mais devant la difficulté à démontrer cette dernière, un certain nombre de travaux ont été initiés aboutissant à des équivalences entre des théories de jauge topologiques, intrinsèquement plus simples que la théorie de super Yang-Mills, et des modèles de théorie des cordes topologiques, eux aussi plus simples que les théories des supercordes usuelles.
L'un des exemples les plus connus d'une telle équivalence est la transition géométrique de Gopakumar/Vafa[réf. nécessaire] au cours de laquelle la théorie de Chern-Simons avec groupe de jauge SU(N) formulée sur la sphère à trois dimensions S3 est équivalente dans la limite
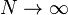
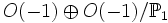
Les avatars topologiques de la correspondance AdS/CFT présentent deux avantages pratiques par rapport à cette dernière
- D'une part ils sont relativement plus simples à prouver : les théories de cordes topologiques étant naturellement reliées à l'évaluation d'invariants topologiques des espaces sur lesquelles elles sont formulées, les prédictions issues de la théorie de jauge topologique peuvent être soumises à une analyse minutieuse de la part des mathématiciens.
- Par ailleurs, un certain nombre de travaux[réf. nécessaire] ont pu montrer que certaines observables des théories effectives des théories de supercordes standards peuvent être calculées en utilisant des théories de corde topologiques. De cette manière il est alors possible d'effectuer une relation entre une théorie de jauge topologique et une théorie de jauge standard. Un exemple célèbre est la correspondance de Dijkgraaf/Vafa qui établit de cette manière une relation entre la théorie effective non-perturbative d'une théorie de Yangs-Mills supersymétrique N = 1 et une théorie de matrices aléatoires. La correspondance, qui au final est formulée uniquement dans un contexte de théories de jauge, a pu être par la suite démontrée complètement[réf. nécessaire] en utilisant uniquement les outils de la théorie quantique des champs. Ce dernier exemple illustre comment la théorie des cordes pourrait être utile d'un point de vue formel à la compréhension des aspects non-perturbatifs des théories de jauges quand bien même elle pourrait faillir d'un point de vue phénoménologique à décrire notre univers.
Le Landscape
Les théories des cordes admettent un grand nombre de solutions à leurs équations qui sont autant d'univers cohérents du point de vue de ces théories. Face à cette multitude, deux positions existent dans la communauté des scientifiques travaillant dans ce domaine
- La position orthodoxe consiste à considérer que cette multitude pose un problème de prédictivité de la théorie. Néanmoins cette multitude serait issue d'un manque de contrôle sur les phénomènes non-perturbatifs existant dans la théorie et qu'une meilleure compréhension de ceux-ci devrait aboutir à l'élimination naturelle d'un grand nombre de solution pour ne laisser émerger en définitive que quelques modèles en accord avec les observations actuelles.
- Un nouveau point de vue, initié par les travaux de Michael Douglas considère qu'il est possible qu'intrinsèquement la théorie des cordes admette un grand nombre de solutions distinctes mais que dans cet ensemble de solutions certaines caractéristiques génériques soient statistiquement plus probables. Par exemple, un grand nombre de travaux cherchent à déterminer si la faiblesse de la constante cosmologique est statistiquement favorisée, ou encore si le groupe de jauge
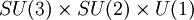
Les différentes théories des cordes
Il existe plusieurs théories des cordes :
- La théorie bosonique des cordes à 26 dimensions. C'est la théorie originale des cordes et la plus simple. La formulation de la théorie sur sa feuille d'univers ne contient que des bosons d'où son nom. Elle contient un tachyon (particule hypothétique dont l'énergie est mesurée par un nombre imaginaire pur et la masse, par un nombre réel), ce qui est une indication que la théorie est instable, et donc impropre à décrire la réalité. Elle est toutefois utile pédagogiquement pour se familiariser avec les concepts fondamentaux que l'on retrouve dans des modèles plus réalistes. En particulier au niveau de masse nulle elle fait apparaître le graviton. Elle admet des cordes ouvertes ou fermées.
- Cinq théories des supercordes à 10 dimensions, qui ne possèdent pas de tachyons et qui supposent l'existence d'une supersymétrie sur la feuille d'univers des cordes aboutissent à l'existence de supersymétries dans l'espace-cible :
- I : cordes ouvertes ou fermées, groupe de symétrie SO(32)
- IIA : cordes fermées uniquement, non-chiralité
- IIB : cordes fermées uniquement, chiralité
- HO : cordes fermées uniquement, hétérodicité, groupe de symétrie SO(32)
- HE : cordes fermées uniquement, hétérodicité, groupe de symétrie E8×E8
- La théorie M, aboutissement de ces théories
Les théories des supercordes se distinguent de la première par l'existence d'une symétrie supplémentaire, la supersymétrie, laquelle s'est avérée nécessaire lorsque l'on a souhaité incorporer les fermions (la matière) dans la théorie bosonique des cordes.
Il semblerait que ces cinq théories soient différentes limites d'une théorie encore mal connue, reposant sur un espace à 11 dimensions (10 spatiales et une temporelle), appelée théorie M, laquelle admettrait la supergravité maximale développée dans les années 1970 comme théorie effective de basse énergie. Cette hypothèse a été proposée par Horava et Witten dans les années 1990 et a amené l'introduction d'autres objets étendus en plus des cordes. On parle de p-branes, p étant un entier qui indique le nombre de dimensions spatiales de l'objet en question. Elles sont décrites perturbativement comme les sous-espaces sur lesquels vivent les extrémités de cordes ouvertes. L'étude du spectre montre que des D1, D3, D5, D7 et D9 branes peuvent être incorporées dans un espace-cible décrit par la théorie IIB tandis que dans un espace où vivent des cordes de type IIA on peut introduire des branes de type D0, D2, D4, D6 et D8. Notons que les D1 ont le même nombre de dimensions qu'une corde fondamentale (notée usuellement F1). Bien qu'étant deux objets distincts, une symétrie non-perturbative de la théorie IIB, appelée S-dualite, qui a subi un nombre important de vérifications indirectes, possède la propriété d'échanger D1 brane avec la F1.
Les Branes
Une brane, ou plus exactement, une p-brane est un objet étendu en théorie des cordes. Le p est le nombre de dimensions spatiales dans laquelle la brane a des extensions. Il faut rajouter à ce nombre une dimension temporelle pour obtenir le nombre total de dimensions. Par exemple, une 1-brane est une brane à une seule dimension spatiale mais deux dimensions au total. Elles correspondent donc à des surfaces d'univers. Une 2-brane est une brane à une dimension temporelle et deux dimensions spatiales.
Cosmologie branaire
Plusieurs modèles cosmologiques ont émergé de l'introduction des branes en théorie des cordes. L'idée générale de la cosmologie branaire est que notre univers serait confiné sur une 4-brane. Ceci signifie que les particules de matière (quarks, électrons, etc...) et les interactions fondamentales autres que la gravitation (transportées par les particules telles le photon, le gluon, etc...) ne sont autorisés à se déplacer qu'à l'intérieur de la brane tandis que la gravitation a la possibilité de se déplacer également dans l'espace-temps complet (on dit aussi le bulk en anglais) dont la brane ne représente qu'un sous-espace.
Par ailleurs dans le cadre du modèle du Big Bang une idée a été introduite récemment comme alternative à l'inflation cosmique pour décrire les tout premiers instants de l'histoire de l'univers, le modèle ekpyrotique. Dans ce modèle, l'expansion initiale est due à la collision d'une brane et d'une anti-brane, ce qui libère l'énergie nécessaire à l'expansion de l'univers. Ce modèle prédit la possibilité d'autres collisions ce qui entrainerait d'autres Big Bang. Néanmoins il n'a pas suscité l'unanimité au sein de la communauté des cosmologistes et l'inflation cosmique reste le mécanisme principalement considéré pour décrire les premiers instants.
Surface d'univers
La surface d'univers est la surface couverte par le mouvement d'une corde. Elle est, plus exactement, une 1-brane.
Des dimensions supplémentaires
Selon la théorie des cordes, notre monde, apparemment tridimensionnel, serait non pas constitué de trois dimensions spatiales, mais de 10, 11, ou même 26 dimensions[2]. Sans ces dimensions supplémentaires, la théorie s'écroule. En effet, la cohérence mathématique impose la présence de dimensions supplémentaires. La raison pour laquelle elles restent invisibles, est qu'elles seraient enroulées par le procédé de la réduction dimensionnelle a une échelle microscopique (des milliards de fois plus petit qu'un atome !!), ce qui ne nous permettrait pas de les détecter.
En effet, si on imagine un cable vu de loin, celui ci ne représente qu'une droite sans épaisseur, un objet unidimensionnel. Si l'on se rapproche assez près, on s'aperçoit qu'il y a bien une deuxieme dimension, celle qui s'entoure autour du câble! D'après la théorie des cordes, le tissu spatial pourrait avoir de très grandes dimensions comme nos trois dimensions habituelles mais également de petites dimensions enroulées sur elles même.
Espaces de Calabi-Yau
Les espaces de Calabi-Yau sont des variétés qui jouent le rôle des dimension enroulées. C'est une forme extrêmement complexe constituée à elle seule de six dimensions. Grâce à eux, on se retrouve bien avec dix dimensions : nos quatre dimensions habituelles + les six des espaces de Calabi-Yau.
Théorie M
La théorie M, alliée à la supergravité à onze dimensions, est l'aboutissement des cinq théories des cordes. Cette théorie semble bien être la théorie de tout. Elle a été découverte par Edward Witten, en 1995. Lors de la conférence Strings'95, il démontra que si on élevait la constante de couplage de la corde Hétérotique E, d'un nombre négatif, à un nombre positif, cela mettait en évidence la supergravité[3]. L'origine du nom de la Théorie M est assez incertaine: certain prétendent qu'ils s'agit du W de Witten inversé. D'autres pensent qu'il s'agit du M de Master Theory. Les detracteurs de cette théorie disent parfois que cela veut dire Minable Theory.
La constante de couplage des cordes
En théorie des cordes, la constante de couplage est un nombre positif qui détermine la probabilité avec laquelle deux cordes peuvent se fondre en une, puis se re-séparer. C'est grâce à cette notion que la Théorie M fut découverte.
Supersymétrie
La supersymétrie est une symétrie en physique des particules. Elle établit un lien très solide entre les particules dotées d'un spin entier, et celles dotées d'un spin demi-entier. Dans ce contexte, les fermions sont associés à un autre type de particule : le superpartenaire. Les superpartenaires sont des grosses particules en tout point identiques à leur associé, sauf au niveau du spin : celui du superpartenaire diffère d'une demi-unité.
Supergravité
La supergravité est une théorie qui allie la supersymétrie à la relativité générale. Son fonctionnement est donc basé sur 11 dimensions.
Prédictions des théories des cordes
- Le graviton, boson (i.e. médiateur) de la gravitation serait une particule de spin 2 et de masse nulle (conformément à la physique quantique). Sa corde a une amplitude d'ondes nulles.
- Il n'y a pas de différences mesurables entre des cordes qui s'enroulent autour d'une dimension et celles qui se déplacent dans les dimensions (i.e., les effets dans une dimension de taille R sont les mêmes que dans une dimension de taille 1/R).
Limitations et controverses concernant les théories des cordes
La théorie des cordes a suscité, et suscite encore, beaucoup d'espoirs. Cependant un certain nombre de points importants semblent poser problème et sont toujours très controversés. Aucune de ces controverses n'invalide définitivement la théorie, mais elles montrent que cette théorie a encore besoin d'évoluer, de se perfectionner et de corriger ses faiblesses.
- Non prédiction et difficultés d'interprétation de l'énergie noire.
Une des faits expérimentaux majeurs observés ces dernières années est que l'univers est en expansion accélérée. Une énergie noire, de nature inconnue, a été postulée pour expliquer cette accélération. Cette énergie noire peut être vue également comme une constante cosmologique positive. La théorie des cordes n'a pas prévu l'accélération de l'expansion de l'univers car cette théorie mène naturellement vers des univers à constante cosmologique négative ou nulle [4]. Rendre la théorie des cordes compatible avec une constante positive s'est avéré très ardu et n'a été effectué qu'en 2003 par un groupe de l'université de Stanford[5]. Mais une des conséquences de ce travail est qu'il existe de l'ordre de 10500 théories des cordes possibles, donnant un "paysage" (landscape) de théories plutôt qu'une théorie unique. L'existence de ce nombre énorme de théories différentes - qui ont toutes la même validité théorique - mène directement à l'hypothèse d'un multivers, voire au principe anthropique, ce qui gène ou intrigue nombre de physiciens.
Joseph Polchinski observe cependant[6] que Steven Weinberg a prédit dans les années 1980 une constante cosmologique non-nulle en faisant l'hypothèse d'un multivers, ce qui est précisément une conséquence possible de la théorie des cordes.
- Irréfutabilité et absence de prédictions
Selon Peter Woit[7], une théorie des cordes ne peut même pas être fausse. En effet, le Landscape de théories permet d'ajuster les constantes libres de la théorie des cordes de manière à s'accommoder de pratiquement n'importe quelle observation, connues ou à venir. Par exemple, si le LHC ne détecte pas les particules superpartenaires, il sera possible de modifier la théorie pour rendre ces particules plus lourdes afin d'expliquer leur non-détection. Cette flexibilité rend également très difficile de faire des prédictions de phénomènes physiques pouvant tester et valider la théorie des cordes. De plus, on ne sait pas s'il sera possible d'effectuer des expérimentations sur les dimensions supplémentaires de l'Univers.
Si la théorie des cordes est difficilement réfutable, elle peut cependant être vérifiable. Récemment, des hypothèses ont été élaborées pour vérifier la théorie des cordes (lien).
- Indépendance de la géométrie de fond
La théorie des cordes est actuellement décrite comme une théorie semi-classique. C'est-à-dire que considérant un environnement (géométrie de fond plus matière éventuelle) fixé, la formulation comme modèle sigma permet de trouver et d'étudier les excitations des cordes seulement au voisinage de cette géométrie. Un analogue en mécanique quantique de cette situation est l'étude de l'atome d'hydrogène baignant dans un champ électrique de fond (ce qui permet par exemple d'étudier l'émission spontanée mais pas stimulée).
Un certain nombre de points sont cependant à noter :
- - L'invariance par difféomorphismes de l'espace cible fait partie des symétries de la théorie.
- - Pour la consistance quantique de la théorie, l'environnement doit satisfaire aux équations de la relativité générale.
- - Parmi les excitations de la corde on trouve une particule, le graviton, qui possède les nombres quantiques nécessaires à la description d'une métrique générale comme état cohérent de gravitons.
- - Les états de la théorie sont des fonctions d'onde correspondant à un nombre fixé de cordes.
Les deux premiers points montrent que la théorie est parfaitement compatible avec la relativité générale. Le deuxième point est analogue dans le cas de l'atome d'hydrogène avec la nécessité pour le champ de fond de satisfaire aux équations de Maxwell. Afin de se libérer de ces contraintes sur l'environnement, et par analogie avec la seconde quantification dans le cas des particules qui aboutit à la théorie quantique des champs, il est donc désirable de posséder une théorie de champs de cordes qui correspond à la quantification de ces fonctions d'ondes de cordes. Cette formulation existe mais les complications techniques dues à la nature étendue des cordes rendent la recherche de solutions exactes à ses équations extrêmement difficile mathématiquement, et donc son impact sur les développements en théorie des cordes est encore limité par comparaison à l'impact qu'a eu la théorie quantique des champs en physique des particules.
Notons finalement qu'en gravitation quantique à boucles qui est un autre candidat à une description quantique de la gravité (mais qui ne permet pas d'incorporer des champs de matière cependant) la formulation de la théorie est explicitement indépendante de la géométrie de fond mais il n'est pas encore établi qu'elle respecte l'invariance de Lorentz.
- Finitude de la théorie non formellement démontrée.
La théorie des cordes est souvent présentée comme ayant résolu le problème des "quantités infinies", qui apparaissent dans la théorie quantique des champs ou dans la relativité générale. Ceci est un succès majeur de la théorie des cordes, et l'exactitude de sa démonstration est donc un enjeu important. Une preuve a été publiée en 1992 par Stanley Mandelstam que certains types de divergences n'apparaissent pas dans les équations la théorie des cordes. Toutefois, comme Mandelstam l'accorde lui-même dans une lettre à Carlo Rovelli[8], il n'est pas exclu que d'autres types d'infinis puissent apparaitre.
En 2004, Nathan Berkovits parvient à démontrer que toute forme d'infini est impossible, et cela à tout ordre d'approximation, mais en reformulant la théorie des cordes, notamment en ajoutant un certain nombre de présupposés supplémentaires.
Malgré l'absence de preuve formelle, peu de théoriciens remettent en doute la finitude de la théorie des cordes. Mais certains, comme Lee Smolin pensent que la difficulté à aboutir à une preuve définitive témoigne d'un problème fondamental à ce niveau.
Notes
- ↑ la théorie M, ne serait elle-même pas une théorie de cordes mais plutôt de membranes, c'est-à-dire des objets dont le volume d'univers possède trois dimensions.
- ↑ 10 dimension dans les cinq théories des cordes conventionnelles ; 11 D avec la théorie M et la supergravité ; et 26 D dans le cas de la théorie des cordes bosoniques
- ↑ (en)Les équations de Witten
- ↑ Edward Witten : This means that there is no classical way to get de Sitter space from string theory or M-theory. Quantum gravity in de Sitter Space (lien)
- ↑ Renata Kallosh, Andreï Linde, Shamit Lachru, Sandip Trivedi De Sitter vacua in String Theory (lien)
- ↑ http://www.americanscientist.org/BookReviewTypeDetail/assetid/54416
- ↑ Peter Woit. Not Even Wrong: The Failure of String Theory and the Search for Unity in Physical Law. Basic Books, 2006
- ↑ Lee Smolin The Trouble With Physics: The Rise of String Theory, the Fall of a Science, and What Comes Next. Houghton Mifflin. 2006 ISBN 978-0-618-55105-7.



















































