John von Neumann - Définition

|
|
| John von Neumann dans les années 1940 | |
| Nom : | né Margittai Neumann János Lajos |
|---|---|
| Naissance : | 28 décembre 1903 Budapest |
| Décès : | 8 février 1957 (à 53 ans) |
| Nationalité : |
|
| Profession : | professeur, conseiller du gouvernement |
| Occupation : | mathématicien, physicien, économiste |
| Formation : | Université de Budapest, École polytechnique de Zurich |
John von Neumann, mathématicien et physicien américain d'origine hongroise, a apporté d'importantes contributions tant en mécanique quantique, qu'en analyse fonctionnelle, en théorie des ensembles, en informatique, en sciences économiques ainsi que dans beaucoup d'autres domaines des mathématiques et de la physique. Il a de plus participé aux programmes militaires américains.
Biographie
Benjamin d'une fratrie de trois, il s'appelle tout d'abord Neumann János Lajos (les Hongrois placent les noms de famille en tête) à Budapest en Autriche-Hongrie. Il est le fils de Neumann Miksa (Max Neumann), un avocat-banquier, et de Kann Margit (Marguerite Kann), tous deux juifs non-pratiquants[réf. nécessaire].
János est un enfant prodige : à six ans, il converse avec son père en grec ancien et peut mentalement faire la division d'un nombre à huit chiffres. Une anecdote rapporte qu'à huit ans, il a déjà lu les quarante-quatre volumes de l'histoire universelle de la bibliothèque familiale et qu'il les a entièrement mémorisés : doté d'une mémoire eidétique, il sera capable de citer de mémoire des pages entières de livres lus des années auparavant. Il entre au lycée luthérien de Budapest (Budapesti Evangélikus Gimnázium) en 1911.
En 1913, son père achète un titre nobiliaire austro-hongrois et Neumann János devient János von Neumann qui sera anglicisé, dans les années 1930, en John von Neumann au moment de l'émigration aux États-Unis (alors que ses frères choisiront pour patronymes Newman et Vonneumann).

C'est âgé d'à peine 23 ans qu'il reçoit son Ph.D. en mathématiques (avec des mineures en physique expérimentale et en chimie) de l'Université de Budapest. En parallèle, il obtient le diplôme de l'école polytechnique fédérale de Zurich à la demande de son père et sur les conseils de Theodore von Karman, désireux que son fils s'investisse dans un secteur plus rémunérateur que les mathématiques[réf. nécessaire].
Entre 1926 et 1930, il est privatdozent à Berlin et à Hambourg. Il travaille également à Göttingen avec Robert Oppenheimer sous la direction de David Hilbert. Durant cette " période allemande ", l'une des plus fécondes de sa vie, il côtoie également Werner Heisenberg et Kurt Gödel.
En 1930, Von Neumann est professeur-invité à l’Université Princeton. Puis, de 1933 à sa mort en 1957, il est professeur de mathématiques à la faculté de l'Institute for Advanced Study qui vient d'être créée. Il y rejoint donc Albert Einstein et Kurt Gödel.
Il se marie une première fois en 1930, avec Mariette Kövesi avec laquelle il a une fille, Marina née en 1935 (plus tard professeur à l'Université du Michigan et conseillère économique du président Nixon). Il aurait proposé le mariage à Mariette en remarquant : " On sera capables de s'amuser tous les deux, vu à quel point on aime boire "[1]. Ils divorcent en 1937. Un an plus tard, John von Neumann épouse Klara Dan.
C'est un hédoniste et un bon vivant dont on dit qu'il sait tout compter, sauf les calories qu'il ingurgite. Il aime plaisanter et raconter des blagues salaces. Il regarde les jambes des femmes avec une telle insistance que certaines des secrétaires à Los Alamos mettent un carton ou une feuille de papier protectrice devant leur bureau[1].
En 1937, il est naturalisé Américain. La guerre devenant inévitable, il s'oriente vers les mathématiques appliquées (statistiques, analyse numérique, balistique, détonique, hydrodynamique). Il développe la méthode de Monte-Carlo pour faire l'économie de temps de calcul et participe à la création des premiers ordinateurs pour raccourcir ce temps de calcul qui devient une ressource essentielle de la guerre moderne.
À partir de 1940 et jusqu'à sa mort, il est membre du comité consultatif scientifique du Ballistic Research Laboratory (Laboratoire en recherches balistiques de l'US Army). De 1943 à 1955, il est consultant scientifique au Laboratoire national de Los Alamos et participe au projet Manhattan. Il entame ses travaux sur la logique probabiliste au lendemain d’une conférence Macy en 1946, où Walter Pitts avait présenté les modèles biologiques. Plus tard, avec Pitts et Warren McCulloch, il introduisit une notion d’aléatoire dans les réseaux de façon à les rendre capables de fonctionner en présence d’erreurs et de bruits affectant les calculateurs élémentaires et leurs connexions.
En 1952, il devient membre du Comité consultatif général (General Advisory Committee) de la Commission américaine à l'énergie atomique (United States Atomic Energy Commission) dont il prend la direction en 1955. Il est l'un des théoriciens de la guerre froide et de la destruction mutuelle assurée.
Il décède dans d'atroces souffrances, en 1957, d'un cancer des os ou du pancréas, probablement causé par une surexposition aux rayons X lors de tests sur la bombe A auxquels il a assisté dans le Pacifique ou lors de travaux sur des armes nucléaires au Laboratoire national de Los Alamos[réf. nécessaire].
Contributions
À la logique mathématique
L'axiomatisation des mathématiques sur le modèle des éléments d'Euclide atteint des nouveaux degrés de rigueur et de profondeur à la fin du XIXe siècle, en particulier en arithmétique (Richard Dedekind et Giuseppe Peano) et en géométrie (David Hilbert). Au tournant du XXe siècle, en revanche, la théorie des ensembles, la nouvelle branche des mathématiques créée en particulier par Georg Cantor, est fortement ébranlée par la découverte de paradoxes par Cantor lui même, Cesare Burali-Forti et Bertrand Russell. En 1897 Burali-Forti découvre une construction qui conduira à ce que l'ensemble de tous les ordinaux n'a pas d'ordinal. Russell publie en 1903 son célèbre paradoxe au sujet des ensembles qui n'appartiennent pas à eux-mêmes.
Au cours des vingt annéees qui suivirent, Ernst Zermelo, puis Abraham Adolf Fraenkel et Thoralf Skolem, montrèrent comment axiomatiser la théorie des ensembles de façon à éviter les paradoxes connus, tout en permettant la construction d'ensembles effectivement usités en mathématiques, en particulier les constructions de Cantor. Ceci aboutit finalement à la théorie ZFC (théorie de Zermelo-Fraenkel avec axiome du choix). Cependant ils n'excluent pas la possibilité d'ensembles qui, s'ils ne sont pas paradoxaux, semblent contre-intuitifs comme les ensembles qui appartiennent à eux-mêmes. Dans sa thèse de doctorat, von Neumann énonce l'axiome de fondation qui exclut en particulier cette éventualité, et permet surtout de hiérarchiser l'univers des ensembles. Il propose également la théorie des classes, une reformulation de la théorie ZFC, qui permet de parler de collections d'objets qui ne sont pas nécessairement des ensembles, de façon adéquate à une notion restée assez informelle chez Cantor. Cette théorie a ensuite été améliorée par Paul Bernays puis par Kurt Gödel. Elle est désormais connue sous le nom de Théorie des ensembles de von Neumann–Bernays–Gödel (en abrégé, NBG).
Pour simplifier, on dira que l'axiome de fondation précise que les ensembles doivent être construits progressivement de sorte que, si un ensemble appartient à un autre, alors celui-ci vient avant celui-là et ne peut par conséquent lui appartenir. Afin de prouver que l'addition de ce nouvel axiome n'engendre pas de nouvelle contradiction (du type de Russell), von Neumann introduit une nouvelle méthode de démonstration, la méthode des modèles internes, qui fut illustrée ensuite par Gödel pour montrer la cohérence relative de l'hypothèse du continu, et qui est devenue essentielle dans la théorie des ensembles.
Avec cette méthode et la notion de classe, le système axiomatique de la théorie des ensembles semble totalement satisfaisant et adéquat aux intuitions de Cantor, mais la question se pose de savoir s'il est complet. Une réponse négative est apportée en 1930 par Gödel qui, au congrès international des mathématiques de Konigsberg, annonce son premier théorème d'incomplétude : dans n'importe quelle théorie récursivement axiomatisable, cohérente et capable de " formaliser l'arithmétique ", on peut construire un énoncé arithmétique qui ne peut être ni prouvé ni réfuté dans cette théorie. Von Neumann fut alors l'un des rares à comprendre ce résultat et ses conséquences, en particulier pour le programme de Hilbert auquel il adhérait comme beaucoup de mathématiciens de l'époque. Il fut capable dans le mois qui suivit la conférence de proposer à Gödel la conséquence suivante de son théorème : les systèmes axiomatiques, sous des conditions analogues, sont incapables de démontrer leur propre consistance. C'est le second théorème d'incomplétude de Gödel, que cependant ce dernier connaissait déjà[réf. nécessaire]. Il est probable que von Neumann fut pour beaucoup dans la reconnaissance des travaux de Gödel, et il fut toujours d'une grande aide pour ce dernier.
On doit aussi à von Neumann la notion d'ensemble transitif, ainsi qu'une définition précise et simple de la notion de nombre ordinal en théorie des ensembles, qui permet en particulier la construction des entiers naturels (on parle alors d'ordinal de von Neumann, ou d'entier de von Neumann).
À la mécanique quantique
En 1900, David Hilbert présente sa liste des 23 problèmes dont le sixième porte sur l'axiomatisation de la physique. Dans les années 1930, la mécanique quantique est peu acceptée par les physiciens, pour des raisons tout autant philosophique que technique. D'un coté, le non-déterminisme quantique n'a pas été réduit en dépit des efforts d'Albert Einstein (et ne le sera jamais), d'un autre côté, la théorie est sous-tendue par deux formalisations heuristiques, concurrentes et équivalentes avec, d'une part, la formalisation matricielle de Werner Heisenberg et, d'autre part, l'approche par les équations différentielles ondulatoires d'Erwin Schrödinger. Il manque une formulation mathématique unique, unificatrice et satisfaisante de la théorie.
Von Neumann, en 1926, s'attaque à l'axiomatisation de la mécanique quantique et réalise rapidement qu'un système quantique peut-être considéré comme un point dans un espace de Hilbert analogue de dimension 6N (où N est le nombre de particules, 3 coordonnées spatiales et 3 coordonnées canoniques). Les quantités physiques traditionnelles (position et énergie) peuvent être remplacés par des opérateurs linéaires dans ces espaces.
La physique quantique est désormais réductible aux mathématiques des opérateurs hermitiens linéaires dans un espace de Hilbert.
Par exemple, le fameux principe d'incertitude de Heisenberg selon lequel on ne peut déterminer la position et la vitesse d'une particule équivaut à la non-commutativité de deux opérateurs correspondants. Cette formule mathématique réconcilie Heisenberg et Schrödinger et von Neuman publie en 1932 son classique Les Fondements mathématiques de la mécanique quantique (The Mathematical Foundations of Quantum Mechanics). Si cette axiomatisation plaît énormément aux mathématiciens pour son élégance, les physiciens lui préfèrent celle de Paul Dirac, publiée en 1930[2] et qui s'appuie sur une étrange fonction, la fonction δ de Dirac. Sa théorie sera durement critiquée par von Neumann.
À l'économie
Jusqu'aux années 1930, l'économie utilise un grand nombre de données chiffrées mais sans réelle rigueur scientifique. Elle ressemble à la physique du XVIIe siècle : dans l'attente d'un langage et d'une méthode scientifique pour exprimer et résoudre ses problèmes. Alors que la physique a trouvé la solution dans le calcul infinitésimal, von Neumann propose pour l'économie, dans un souci axiomatique qui le caractérise, la théorie des jeux et la théorie de l'équilibre général.
Sa première contribution significative, en 1928, est l'algorithme MinMax (aussi appelé " minimax " suivant l'usage anglophone) dans un théorème qui énonce que, dans un jeu à somme nulle avec information parfaite (les joueurs savent les stratégies possibles des autres et leurs conséquences), il y a une stratégie possible pour minimiser les pertes maximales. Cette stratégie est un optimum pour les deux joueurs si leurs minmax sont égaux ou de signes contraires. Le jeu n'en vaut pas la chandelle si la valeur commune est égale a zéro.
Von Neumann améliore par la suite sa théorie pour y inclure les jeux avec asymétrie d'information et les jeux avec plus de deux joueurs. Son travail aboutit en 1944 avec la publication, en collaboration avec Oskar Morgenstern, de ce qui est devenu un classique de l'économie : La Théorie des jeux et comportements économiques (The Theory of Games and Economic Behavior). On y trouve en particulier le premier emploi du raisonnement par induction.
Sa seconde contribution essentielle à la science économique est la solution, formulée en 1937, d'un problème formulé en 1874 par Léon Walras concernant l'existence d'un point d'équilibre dans les modèles mathématiques d'un marché basé sur l'offre et la demande. Il trouve la solution en appliquant le théorème du point fixe de Brouwer. L'importance toujours actuelle des travaux sur le problème de l'équilibre général et la méthodologie sous-jacente des théorèmes de point fixe est soulignée par l'attribution du prix "Nobel d'économie" en 1972 à Kenneth Arrow et 1983 à Gérard Debreu.
À l'armement atomique
En 1937, peu après l'obtention de la citoyenneté américaine, il s'intéresse aux mathématiques appliquées, devient rapidement l'un des principaux experts en matière d'explosifs et est conseiller de l'US Navy.
L'une de ses découvertes tient à ce que des bombes de " large dimension " ont un effet dévastateur plus important si elles explosent en hauteur plutôt qu'au sol (ce que les média résumeront alors en " von Neumann a découvert que c'est mieux de rater sa cible plutôt que de l'atteindre "). Cela sera mis en pratique lors de l'explosion des premières bombes atomiques les 6 et 9 août 1945, von Neumann ayant calculé l'altitude précise pour maximiser l'étendue des dommages causés.
Dans le cadre du projet Manhattan, il est chargé du calcul des lentilles explosives nécessaires à la compression du noyau en plutonium de l'essai Trinity et de Fat Man, la bombe A larguée sur Nagasaki.
À cette époque, il fait également partie du comité chargé de sélectionner les cibles pour la bombe atomique. Le choix initial de von Neumann (le centre de Kyoto, capitale culturelle du Japon) est alors écarté par Henry Stimson, le ministre de la guerre. Roosevelt, président des États-Unis d'alors, a donné comme consigne formelle d'éviter de bombarder Kyoto, ville qui l'avait ébloui lors d'une visite avant la Seconde Guerre mondiale.
Après-guerre, Robert Oppenheimer faisant la remarque que les physiciens avaient " connu le péché " en développant la bombe atomique se voit répliquer par von Neumann : " Parfois on confesse un péché pour s'en attribuer le crédit. "
Il travaille ensuite au développement de la bombe H. Si le dessein qu'il conçoit avec Klaus Fuchs n'est pas celui retenu, il est reconnu qu'il est un pas dans la bonne direction sur la voie poursuivie par Edward Teller et Stanislaw Ulam.
Pendant la guerre, le Laboratoire national de Los Alamos réunit l'élite intellectuelle juive centre-européenne qui a fui le nazisme, Albert Einstein en étant le plus célèbre, et particulièrement l'élite intellectuelle juive hongroise avec, outre John von Neumann, Paul Erd?s, Eugene Wigner, Edward Teller, Leó Szilárd ou Gábor Dénes. Une blague [1] circule alors dans les couloirs selon laquelle non seulement les martiens existent et qu'ils sont doués d'une intelligence surhumaine, mais ils prétendent venir d'un pays inconnu, la Hongrie, et parlent tous une langue inintelligible au reste de l'humanité.
Le développement des bombes A et H nécessite un nombre très important de calculs. C'est surtout dans ce domaine que l'apport de von Neumann va être essentiel.
À l'informatique
Von Neumann a donné son nom à l'architecture de von Neumann utilisée dans la quasi totalité des ordinateurs modernes, l'apport d'autres collaborateurs de l'EDVAC en est par conséquent grandement minimisé (on citera J. Presper Eckert et John William Mauchly parmi d'autres). Cela est dû au fait qu'il est, en 1944, le rapporteur des travaux pionniers en la matière (First Draft of a Report on the EDVAC). Le modèle de calculateur à programme auquel son nom reste attaché et qu'il attribuait lui-même à Turing, possède une unique mémoire qui sert à conserver les logiciels et les données. Ce modèle, extrêmement innovant pour l'époque, est à la base de la conception de nombre d'ordinateurs.
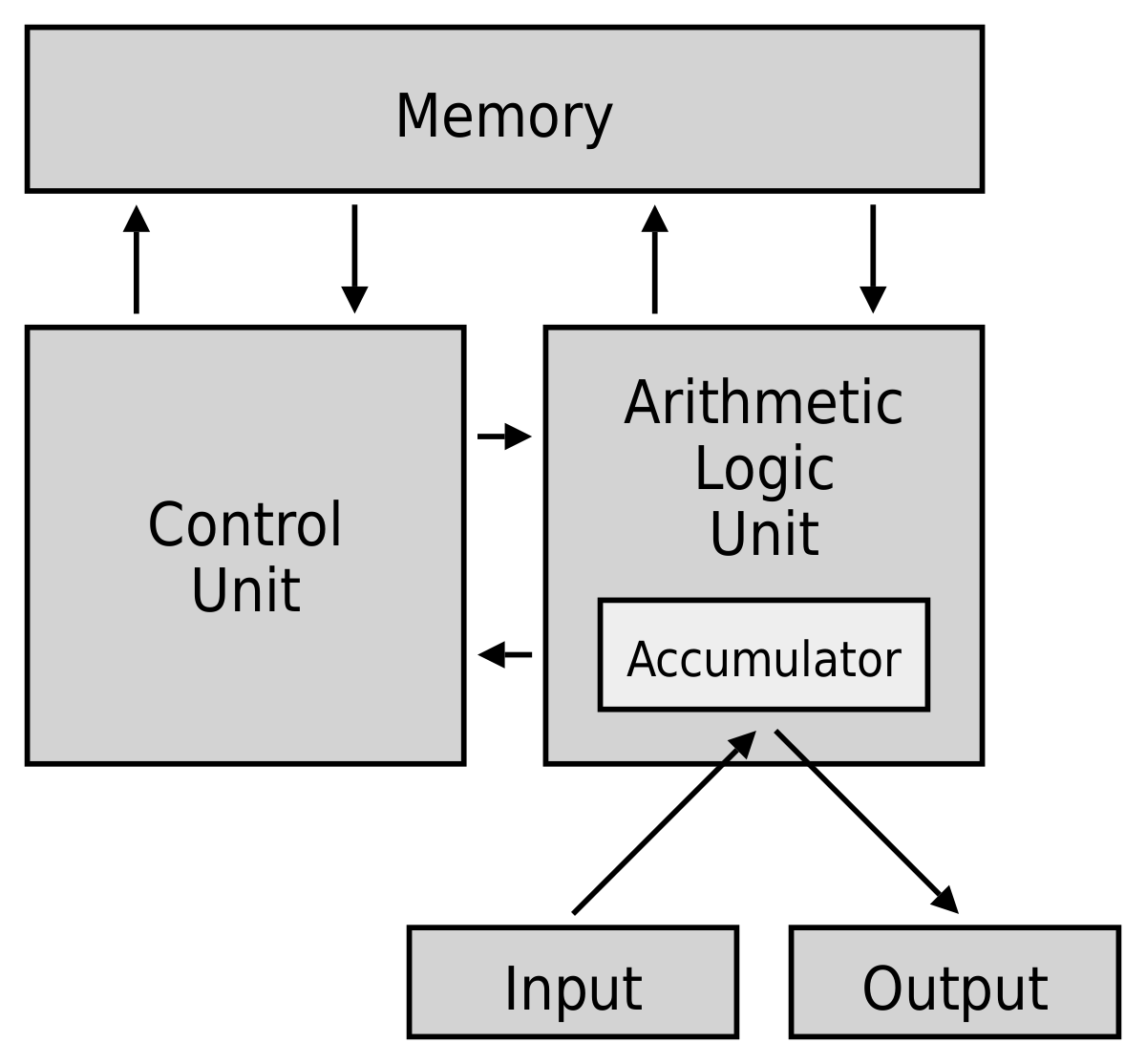
L’architecture de von Neumann décompose l’ordinateur en 4 parties distinctes :
- l’unité arithmétique et logique (UAL) ou unité de traitement, qui effectue les opérations de base ;
- l’unité de contrôle, qui est chargée du séquençage des opérations ;
- la mémoire, qui contient à la fois les données et le programme qui indique à l’unité de contrôle quels calculs faire sur ces données. La mémoire se divise en mémoire vive (programmes et données en cours de fonctionnement) et mémoire de masse (programmes et données de base de la machine) ;
- les dispositifs d’entrée-sortie, qui permettent de communiquer avec le monde extérieur.
Au XXIe siècle, l'utilisation de cette architecture est en régression : les logiciels ne se modifient plus guère eux-mêmes (cela étant considéré comme une mauvaise pratique de programmation), et le matériel prend en compte cette nouvelle donne en séparant aujourd'hui nettement le stockage des instructions et celui des données, y compris dans la mémoire cache.
À l'automatisme cellulaire
Il est également à l'origine du concept novateur d'automate cellulaire afin de construire les premiers exemples d'automates auto-reproductibles introduits dans son œuvre posthume Theory of Self Reproducing Automata et qui a inspiré le jeu de la vie.
Ce qu'en anglais on appelle une von Neumann machine est régi par les principes suivants :
- capable d'accomplir une tâche élémentaire,
- capable de se multiplier pour accomplir cette tâche.
Ce modèle préfigure celui de la reproduction cellulaire et de l'ADN.
Vies sociale et politique

Von Neumann professe de son vivant un anticommunisme viscéral. Il est un collaborateur actif du complexe militaro-industriel américain, consultant pour la CIA et la RAND Corporation. En un mot, il est le cerveau des aspects scientifiques de la guerre froide qui commence alors et qui va durer quarante ans.
Il n'est pas interdit de penser qu'il a beaucoup influencé le stéréotype hollywoodien du savant fou doté d'un fort accent étranger et d'idées réactionnaires, surtout si l'on sait que la destruction mutuelle assurée (mutually assured destruction) qu'il promeut alors a pour acronyme, en anglais, MAD (c'est-à-dire " fou ").
En 1956, peu avant son décès, il reçoit le Prix Enrico Fermi.
Il meurt d'un cancer probablement provoqué par l'exposition aux radiations lors de tests d'explosion de la bombe atomique auxquels il assista. Son lit d'hôpital est sous haute surveillance militaire [1] car on craint que, fortement drogué pour supporter la douleur, il ne divulgue accidentellement des secrets militaires dont il a eu connaissance.
Honneurs et récompenses en son honneur
L'IEEE décerne chaque année une médaille en l'honneur de von Neumann, la (en) IEEE John von Neumann Medal.
Le John von Neumann Theory Prize de l'Institute for Operations Research and Management Science (INFORMS) récompense chaque année un individu ou un groupe pour des contributions fondamentales en recherche opérationnelle et en science du management.
La Société pour les mathématiques industrielles et appliquées (SIAM) donne un prix depuis 1959, intitulé la conférence von Neumann, attribué aux français Jean Leray (1962), René Thom en (1976) et Jacques-Louis Lions (1986).
Un cratère sur la lune porte le nom de von Neumann.
Citation
- " Si les gens ne croient pas que les mathématiques sont simples, c’est uniquement parce qu’ils ne réalisent pas à quel point la vie est compliquée. "
Œuvres
- Fondements mathématiques de la mécanique quantique " The Mathematical Foundations of Quantum Mechanics ", éd. Jacques Gabay, 1992, (ISBN 2876470470)
- Le cerveau et l'ordinateur, Flammarion, coll. " Champs ", 1996, (ISBN 208081284X)
- Théorie générale et logique des automates, Champ Vallon, 1998, (ISBN 2876732327)
- avec Oskar Morgenstern Theory of games and economic behavior, Princeton University Press, 1953 - publié en français sous le titre Théorie des jeux et comportements économiques, Université des Sciences Sociales de Toulouse, 1977.
- Theory of Self-Reproducing Automata, University of Illionois Press, 1966, (ISBN 0598377980)




















































